Atelier distances euclidiennes
Jessika Malko
Décembre 2025
Un atelier présenté par Jessika Malko, validé par Charles Martin
Pour cet atelier, nous allons utiliser des bases de données disponibles dans RStudio via deux librairies.
Ci-dessous, je vous propose deux ressources intéressantes pour comprendre les distances euclidiennes :
- Une première vidéo qui explique comment on calcule les distances à partir de coordonnées (théorème de Pythagore) : https://www.khanacademy.org/math/geometry/hs-geo-analytic-geometry/hs-geo-distance-3d/v/distance-formula
- Et un peu de lecture sur les choix disponibles pour calculer les distances sur les données brutes, la standardisation et d’autres distances : Legendre, P., & Legendre, L. (2012). Numerical Ecology (3rd English edition). Amsterdam: Elsevier. ISBN : 978-0-444-53868-3. spécifiquement le chapitre 2
Un peu de théorie…
Les distances euclidiennes sont une façon de mesurer la distance entre deux points dans un espace géométrique « normal », par exemple un espace à deux dimensions. Une distance plus petite indique des points plus similaires et, au contraire, une distance plus grande indique des points plus dissemblables. Cette analyse ne peut pas être directement comparée d’une étude à l’autre ; elle ne peut être comparée qu’au sein d’un même jeu de données et d’une même analyse.
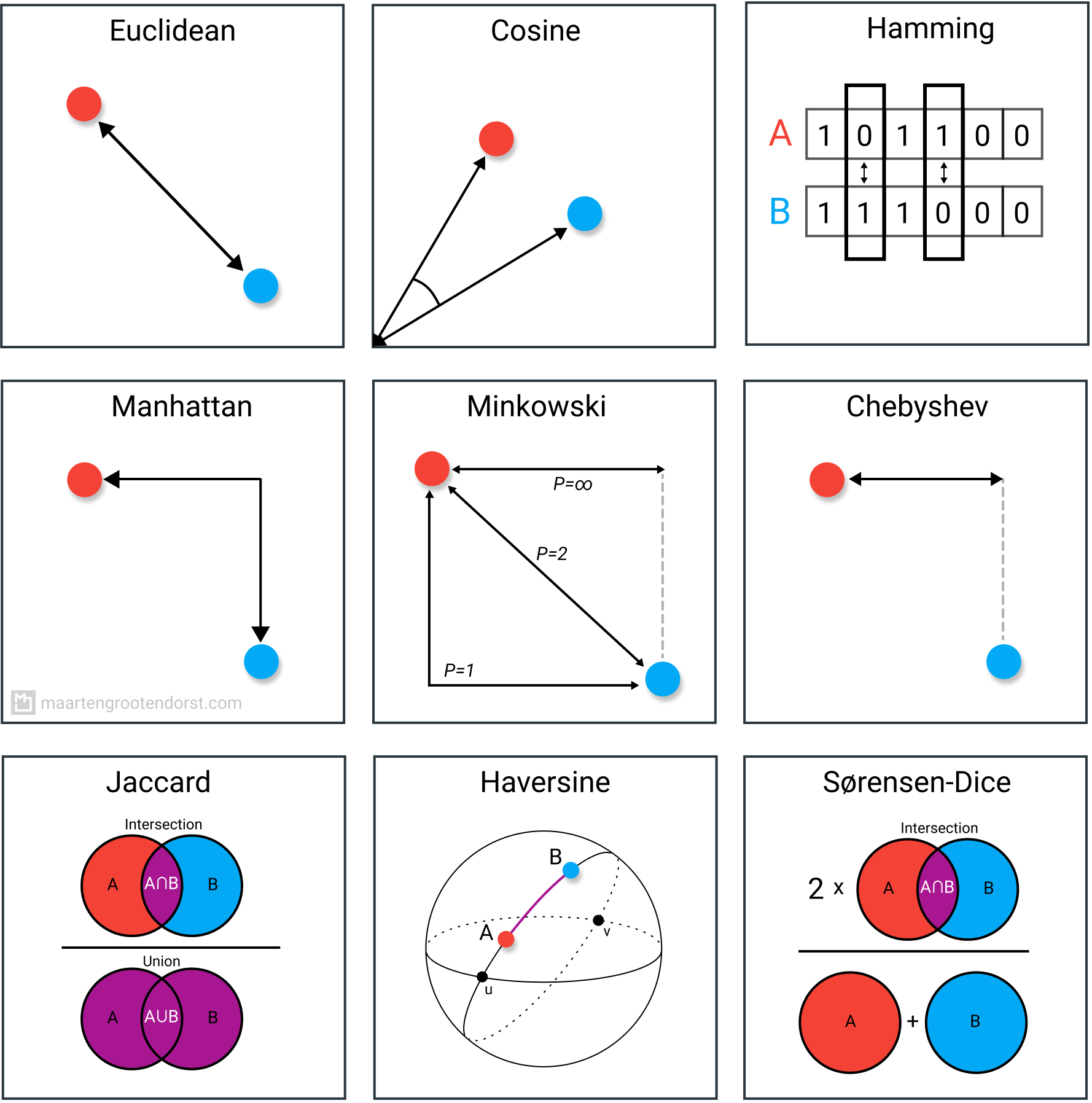
Il existe plusieurs autres distances qui ont été développées pour répondre à des types de données bien précis. On peut penser à Google Maps, qui n’utilise pas les distances euclidiennes, mais plutôt les distances de Manhattan pour vous indiquer le chemin réel à parcourir à travers le réseau routier. Un autre exemple est la distance cosinus, qui mesure la similarité de direction et est couramment utilisée pour comparer des textes. On peut penser, par exemple, aux recherches par mots-clés dans Google Scholar. Bref, vous comprenez l’idée.
Les hypothèses des distances euclidiennes sont les suivantes :
-
La non-négativité : la distance est >= 0.
-
L’identité : la distance de 0 existe seulement si deux points sont identiques.
-
La symétrie : la distance entre A et B est identique à la distance entre B et A.
Les distances euclidiennes constituent une analyse simple et rapide. Elles sont très efficaces pour analyser des données multidimensionnelles. Leur désavantage provient du principe de la Curse of dimensionality, c’est-à-dire qu’elles deviennent moins efficaces à mesure que l’on ajoute des dimensions, puisque les distances ont tendance à se ressembler.
Les étapes de l’analyse se résument à :
1- Préparer notre base de données, soit de gérer les valeurs extrêmes/aberrantes (outliers) et les NAs;
2- normaliser la distribution des données;
3- aggréger les données pour chaque variable à chaque point;
4- centrer-réduire l’ensemble de données données pour contrôler pour les différentes échelles et unitées;
5- et finalement, calculer les distances.
S’il y a une chose que vous devriez retenir de cet atelier, c’est ceci : l’analyse par distance est une analyse très simple. La difficulté réside dans les décisions prises en amont, soit de bien définir la question écologique, de bien définir les points entre lesquels les calculs seront effectués, et de choisir et préparer adéquatement les variables qui définiront ces points.
L’atelier
Débutons! Activez d’abord les librairies et chargez les données des manchots de Palmer.
library(tidyverse)
library(ggplot2)
#install.packages("palmerpenguins") # à installer si ce n'est déjà fait
library(palmerpenguins)
data(penguins)
str(penguins)
tibble [344 × 8] (S3: tbl_df/tbl/data.frame)
$ species : Factor w/ 3 levels "Adelie","Chinstrap",..: 1 1 1 1 1 1 1 1 1 1 ...
$ island : Factor w/ 3 levels "Biscoe","Dream",..: 3 3 3 3 3 3 3 3 3 3 ...
$ bill_length_mm : num [1:344] 39.1 39.5 40.3 NA 36.7 39.3 38.9 39.2 34.1 42 ...
$ bill_depth_mm : num [1:344] 18.7 17.4 18 NA 19.3 20.6 17.8 19.6 18.1 20.2 ...
$ flipper_length_mm: int [1:344] 181 186 195 NA 193 190 181 195 193 190 ...
$ body_mass_g : int [1:344] 3750 3800 3250 NA 3450 3650 3625 4675 3475 4250 ...
$ sex : Factor w/ 2 levels "female","male": 2 1 1 NA 1 2 1 2 NA NA ...
$ year : int [1:344] 2007 2007 2007 2007 2007 2007 2007 2007 2007 2007 ...
Pour ceux qui n’ont jamais travaillé avec ces données, elles comprennent trois espèces de manchots, trois îles, l’année de l’échantillonnage et cinq variables pour décrire chaque individu.
Visualisation des données
C’est toujours une bonne pratique de visualiser les données afin de s’assurer qu’elles sont utilisables pour le type d’analyse que l’on souhaite réaliser. Ici, on examine la distribution des variables que l’on veut utiliser, soit les variables liées au bec, aux nageoires et au poids.
ggplot(data=penguins) +
geom_histogram(aes(bill_length_mm))
`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
Warning: Removed 2 rows containing non-finite outside the scale range
(`stat_bin()`).
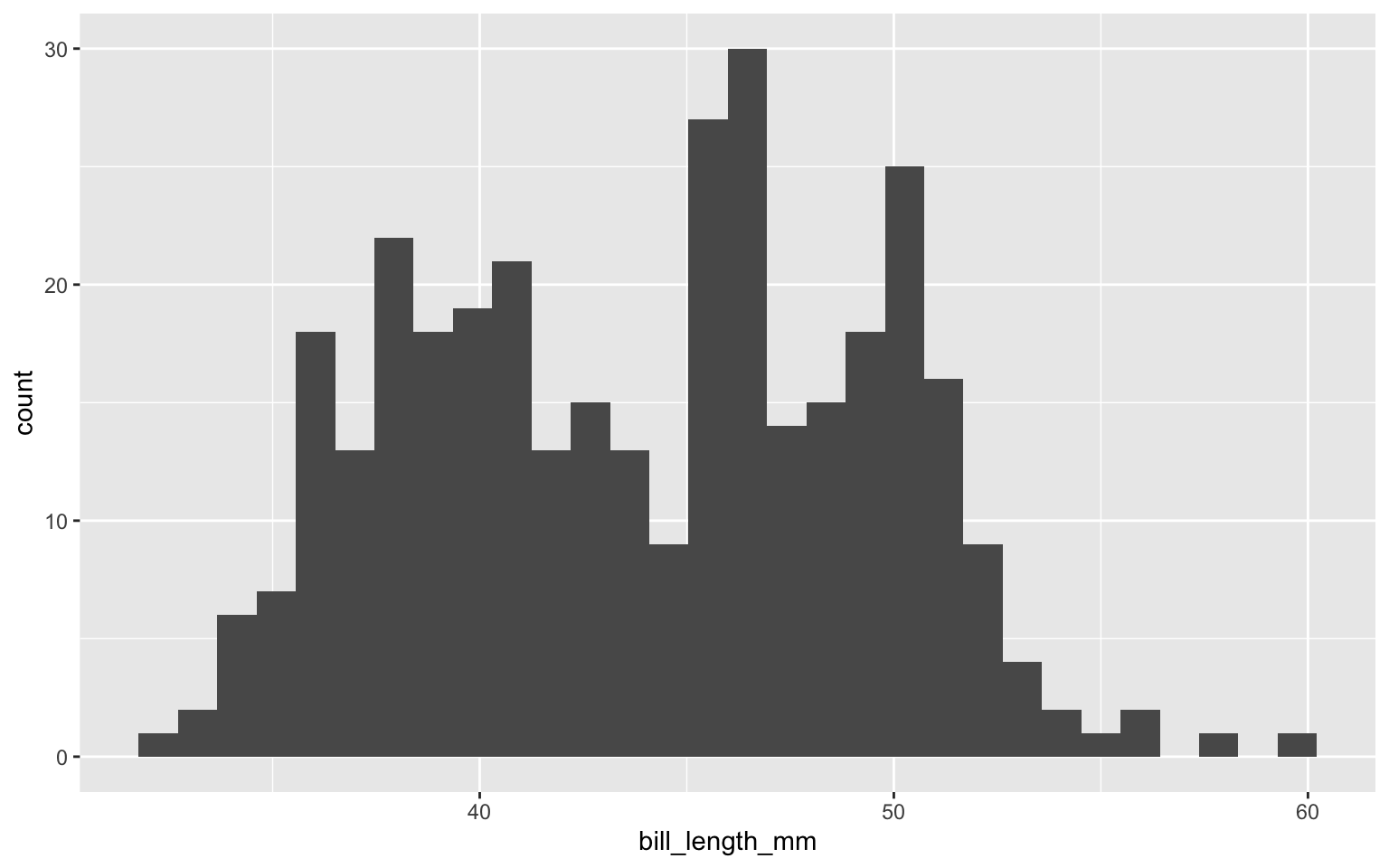
ggplot(data=penguins) +
geom_histogram(aes(bill_depth_mm))
`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
Warning: Removed 2 rows containing non-finite outside the scale range
(`stat_bin()`).
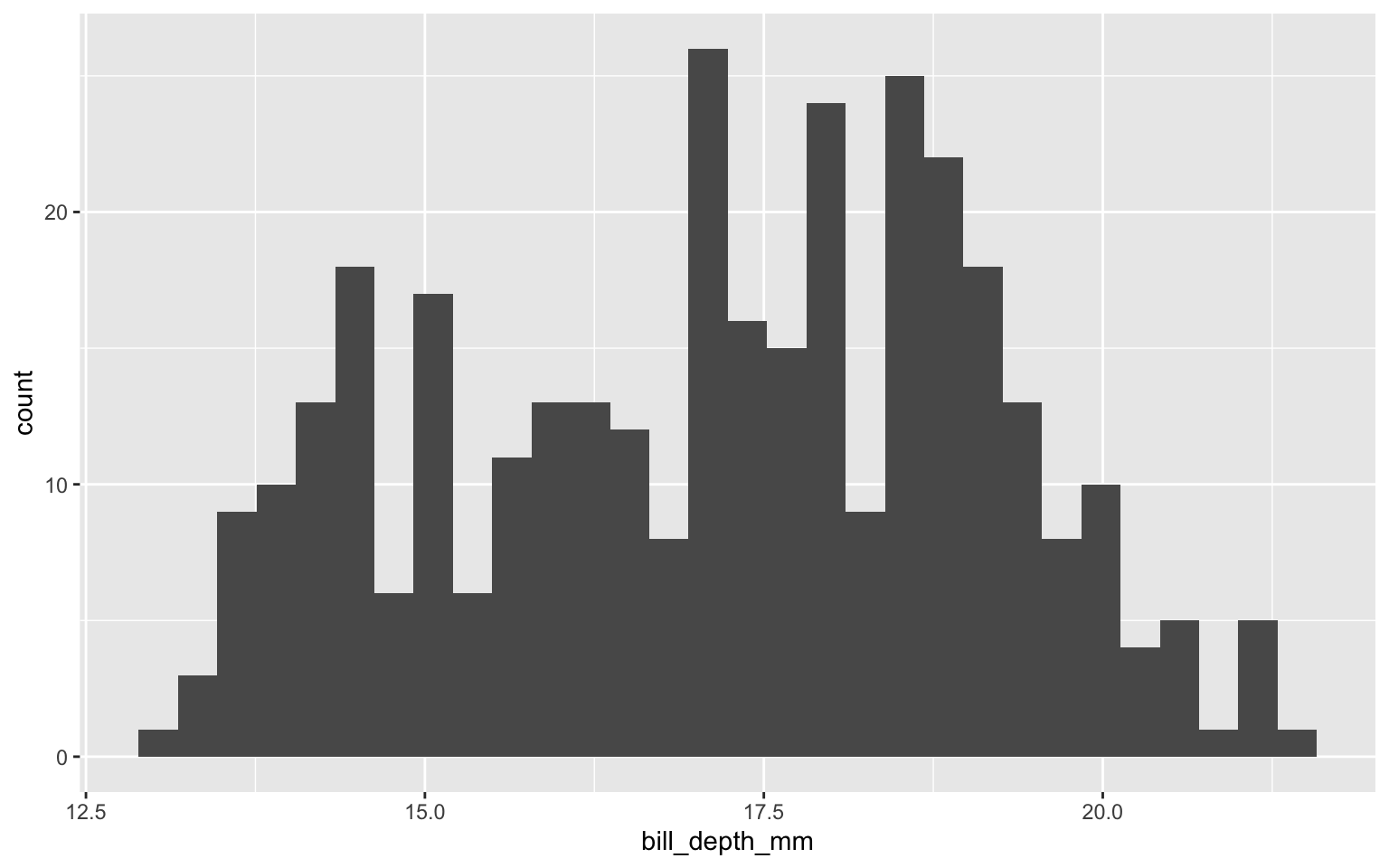
ggplot(data=penguins) +
geom_histogram(aes(flipper_length_mm))
`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
Warning: Removed 2 rows containing non-finite outside the scale range
(`stat_bin()`).
ggplot(data=penguins) +
geom_histogram(aes(body_mass_g))
`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
Warning: Removed 2 rows containing non-finite outside the scale range
(`stat_bin()`).
Rapidement, on peut observer une distribution bimodale pour l’ensemble des variables. Logiquement, on peut se douter que ces tendances sont liées aux différentes espèces.
ggplot(data=subset(penguins, species == "Adelie")) +
geom_histogram(aes(bill_length_mm))
`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
Warning: Removed 1 row containing non-finite outside the scale range
(`stat_bin()`).
ggplot(data=subset(penguins, species == "Gentoo")) +
geom_histogram(aes(bill_length_mm))
`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
Warning: Removed 1 row containing non-finite outside the scale range
(`stat_bin()`).
ggplot(data=subset(penguins, species == "Chinstrap")) +
geom_histogram(aes(bill_length_mm))
`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.
La distribution est déjà beaucoup mieux, mais une distribution bimodale semble persister. C’est ici en lien avec le dimorphisme sexuel. Pour l’atelier, nous allons considérer que l’ensemble des données est normal. Si ce n’était pas le cas, c’est à ce stade que vous voudriez les transformer. Une distribution extrême affectera le poids qu’une variable occupe dans le calcul des distances, comme c’est le cas pour les observations aberrantes (outliers). Il est essentiel d’apprendre à reconnaître ce qui est normal ou non selon votre système d’étude.
Bloc A : la distance entre les espèces
En fonction des variables disponibles dans cette base de données, on peut se poser une première question très simple : quelles espèces de manchots se ressemblent le plus ? Tel que mentionné dans la section Théorie, les distances euclidiennes constituent une analyse très simple qui requiert toutefois un peu de réflexion en amont. Pour répondre à notre question, nous allons considérer que les espèces sont les points entre lesquels nous mesurons les distances, et que les quatre variables de mensuration décrivent ces points.
Étape 1 : déterminer nos points et les variables réponse
summary(penguins) # vérifier les NAs
species island bill_length_mm bill_depth_mm
Adelie :152 Biscoe :168 Min. :32.10 Min. :13.10
Chinstrap: 68 Dream :124 1st Qu.:39.23 1st Qu.:15.60
Gentoo :124 Torgersen: 52 Median :44.45 Median :17.30
Mean :43.92 Mean :17.15
3rd Qu.:48.50 3rd Qu.:18.70
Max. :59.60 Max. :21.50
NA's :2 NA's :2
flipper_length_mm body_mass_g sex year
Min. :172.0 Min. :2700 female:165 Min. :2007
1st Qu.:190.0 1st Qu.:3550 male :168 1st Qu.:2007
Median :197.0 Median :4050 NA's : 11 Median :2008
Mean :200.9 Mean :4202 Mean :2008
3rd Qu.:213.0 3rd Qu.:4750 3rd Qu.:2009
Max. :231.0 Max. :6300 Max. :2009
NA's :2 NA's :2
# créer un objet avec les variables d'intérêt pour faciliter la préparation des données
response_vars <- c("bill_length_mm", "bill_depth_mm", "flipper_length_mm", "body_mass_g")
Nous allons créer une nouvelle base de données afin de gérer les valeurs manquantes (NA) et de conserver uniquement les variables d’intérêt, ce qui facilitera le calcul permettant de déterminer les coordonnées de nos points (nos espèces).
DB <- penguins %>%
drop_na(all_of(response_vars)) # ici, on enlève uniquement les lignes qui contiennent des NAs pour nos 4 variables réponse
Étape 2 : aggréger les individus/réplicas
Cette étape consiste à agréger les observations en une moyenne pour chaque point afin d’en déterminer la coordonnée.
species_means <- DB %>%
group_by(species) %>%
summarize(
across(all_of(response_vars), mean), # fait la moyenne de chaque variable réponse par espèce
.groups = "drop" # n'oubliez pas d'enlever votre sélection ici pour ne pas que ça affecte le reste de votre code
)
Nous préparons ensuite la base de données pour qu’elle soit dans un format utilisable pour les prochaines étapes.
species_input <- species_means %>%
column_to_rownames("species") %>%
select(all_of(response_vars))
Étape 3 : Centrer-réduire
Cette étape consiste à agréger les observations en une moyenne pour chaque point afin d’en déterminer la coordonnée.
species_data <- scale(species_input) %>%
as.data.frame()
#view(species_data) # ici, nos données sont centrées-réduites. les chiffres correspondent à leur écarts type de la moyenne.
Étape 4 : Calculer les distances
species_matrix <- dist(species_data, method = "euclidean") %>%
as.matrix()
#View(species_matrix) # pour ouvrir la matrice dans un nouvel onglet
# ou
round(species_matrix, 2) # pour affichage dans la console
Adelie Chinstrap Gentoo
Adelie 0.00 1.89 3.49
Chinstrap 1.89 0.00 2.88
Gentoo 3.49 2.88 0.00
Les distances n’ont pas d’unités. Elles sont valables uniquement pour notre jeu de données. On peut utiliser la magnitude des différences entre les espèces pour comparer à d’autres études, avec précaution : il faut que les mêmes variables aient été utilisées.
Bloc B : La distance entre les espèces en fonction de leur île
Complexifions la question un peu… quelle est la différence entre les espèces en fonction de leur île ? Nous allons utiliser les mêmes variables réponse response_vars et la même base de données DB, et aller directement à l’étape 2 : agréger nos observations.
# Étape 2 : aggréger les observations
island_means <- DB %>%
group_by(species, island) %>% # ici la sélection espèce ~ île
summarize(across(all_of(response_vars), mean), # ici la moyenne de cette sélection
.groups = "drop")
# Étape 3 : Centrer-Réduire
island_input <- island_means %>%
mutate(species_island = paste(species, island, sep = "_")) %>%
column_to_rownames("species_island") %>%
select(all_of(response_vars))
island_data <- scale(island_input) %>%
as.data.frame()
round(island_data, 2) # visualisation des données centrées-réduites
bill_length_mm bill_depth_mm flipper_length_mm body_mass_g
Adelie_Biscoe -0.69 0.45 -0.65 -0.45
Adelie_Dream -0.79 0.37 -0.58 -0.48
Adelie_Torgersen -0.70 0.49 -0.45 -0.45
Chinstrap_Dream 1.22 0.48 -0.06 -0.41
Gentoo_Biscoe 0.96 -1.79 1.74 1.79
# Étape 4 : Calculer la distance
island_matrix <- dist(island_data, method = "euclidean") %>%
as.matrix()
round(island_matrix, 2)
Adelie_Biscoe Adelie_Dream Adelie_Torgersen Chinstrap_Dream
Adelie_Biscoe 0.00 0.15 0.21 2.00
Adelie_Dream 0.15 0.00 0.19 2.07
Adelie_Torgersen 0.21 0.19 0.00 1.96
Chinstrap_Dream 2.00 2.07 1.96 0.00
Gentoo_Biscoe 4.30 4.27 4.21 3.65
Gentoo_Biscoe
Adelie_Biscoe 4.30
Adelie_Dream 4.27
Adelie_Torgersen 4.21
Chinstrap_Dream 3.65
Gentoo_Biscoe 0.00
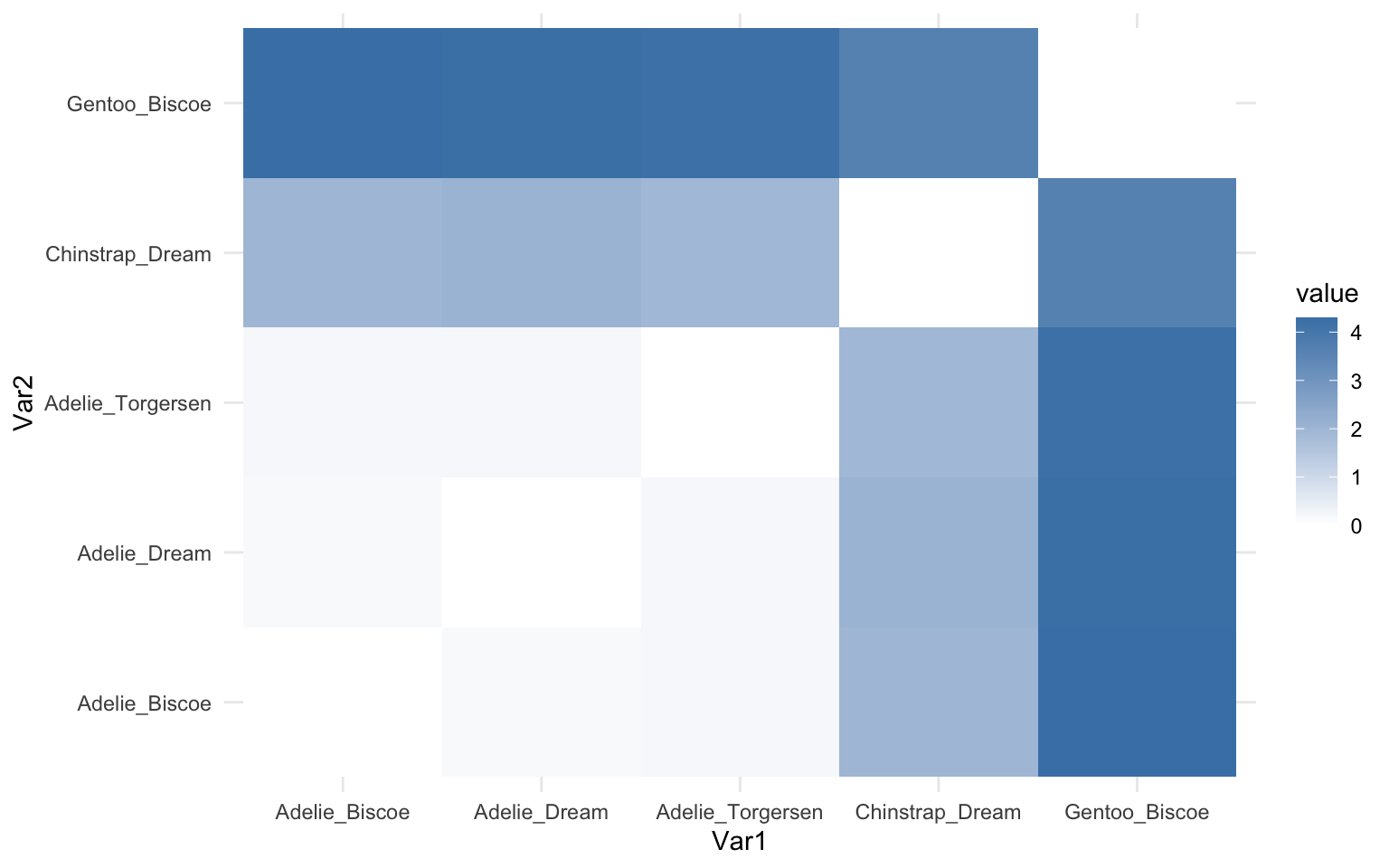
On voit que seule l’espèce Adélie est présente sur les trois îles. On observe également que, pour cette espèce, les individus des îles Dream et Torgersen se ressemblent davantage entre eux qu’avec ceux de l’île Biscoe ; si vous vous rappelez de la carte, cela correspond à la proximité physique des îles.
On peut visualiser les distances à l’aide d’une heatmap, mais ce type de graphique fera davantage sens dans le prochain bloc.
# HEATMAP
library(reshape2)
dist_melt <- melt(island_matrix) # melt() ajuste la matrice de distance en format long pour que ggplot puisse l'utiliser
ggplot(dist_melt, aes(Var1, Var2, fill = value)) +
geom_tile() +
scale_fill_gradient(low = "white", high = "steelblue") +
theme_minimal()
Bloc C : La distance entre les communautés
Dans les deux prochains blocs, nous allons plutôt utiliser les bases de données DUNE et DUNE.ENV de la librairie vegan. Dans ce bloc, nous analyserons la diversité des communautés de plantes. Sachez que vous ne pouvez pas utiliser vos données telles quelles pour calculer les distances : vous devez effectuer une transformation de Hellinger. Cette analyse est d’ailleurs en train de remplacer l’indice de Bray-Curtis, puisqu’elle peut ensuite être combinée à d’autres analyses. Voici les étapes à suivre…
library(vegan)
data(dune)
head(dune) # visualiser le format des données
Achimill Agrostol Airaprae Alopgeni Anthodor Bellpere Bromhord Chenalbu
1 1 0 0 0 0 0 0 0
2 3 0 0 2 0 3 4 0
3 0 4 0 7 0 2 0 0
4 0 8 0 2 0 2 3 0
5 2 0 0 0 4 2 2 0
6 2 0 0 0 3 0 0 0
Cirsarve Comapalu Eleopalu Elymrepe Empenigr Hyporadi Juncarti Juncbufo
1 0 0 0 4 0 0 0 0
2 0 0 0 4 0 0 0 0
3 0 0 0 4 0 0 0 0
4 2 0 0 4 0 0 0 0
5 0 0 0 4 0 0 0 0
6 0 0 0 0 0 0 0 0
Lolipere Planlanc Poaprat Poatriv Ranuflam Rumeacet Sagiproc Salirepe
1 7 0 4 2 0 0 0 0
2 5 0 4 7 0 0 0 0
3 6 0 5 6 0 0 0 0
4 5 0 4 5 0 0 5 0
5 2 5 2 6 0 5 0 0
6 6 5 3 4 0 6 0 0
Scorautu Trifprat Trifrepe Vicilath Bracruta Callcusp
1 0 0 0 0 0 0
2 5 0 5 0 0 0
3 2 0 2 0 2 0
4 2 0 1 0 2 0
5 3 2 2 0 2 0
6 3 5 5 0 6 0
Dune est une base de données de dénombrement de 20 espèces de plantes dans 20 sites. Assurez-vous toujours que vos données sont dans un format de dénombrement où les sites sont en lignes et les espèces en colonnes. On calcule ensuite la proportion relative : c’est la première étape de la transformation de Hellinger.
dune_prop <- dune/rowSums(dune) # calcule les proportions relatives ~ sites
La deuxième étape de la transformation de Hellinger consiste à prendre la racine carrée.
dune_hell <- sqrt(dune_prop) # la racine carrée contrôle pour les espèces dominantes et les absences
N’oubliez pas de préparer une matrice utilisable pour le calcul.
# préparer les données des proportions en matrice
hell_matrix <- as.data.frame(dune_hell)
# Remarquez que c'est une des rares occasion ou on ne fait pas de centrer-réduire; les données sont de la même nature et de la même échelle.
head(hell_matrix)
Achimill Agrostol Airaprae Alopgeni Anthodor Bellpere Bromhord Chenalbu
1 0.2357023 0.0000000 0 0.0000000 0.0000000 0.0000000 0.0000000 0
2 0.2672612 0.0000000 0 0.2182179 0.0000000 0.2672612 0.3086067 0
3 0.0000000 0.3162278 0 0.4183300 0.0000000 0.2236068 0.0000000 0
4 0.0000000 0.4216370 0 0.2108185 0.0000000 0.2108185 0.2581989 0
5 0.2156655 0.0000000 0 0.0000000 0.3049971 0.2156655 0.2156655 0
6 0.2041241 0.0000000 0 0.0000000 0.2500000 0.0000000 0.0000000 0
Cirsarve Comapalu Eleopalu Elymrepe Empenigr Hyporadi Juncarti Juncbufo
1 0.0000000 0 0 0.4714045 0 0 0 0
2 0.0000000 0 0 0.3086067 0 0 0 0
3 0.0000000 0 0 0.3162278 0 0 0 0
4 0.2108185 0 0 0.2981424 0 0 0 0
5 0.0000000 0 0 0.3049971 0 0 0 0
6 0.0000000 0 0 0.0000000 0 0 0 0
Lolipere Planlanc Poaprat Poatriv Ranuflam Rumeacet Sagiproc Salirepe
1 0.6236096 0.0000000 0.4714045 0.3333333 0 0.0000000 0.0000000 0
2 0.3450328 0.0000000 0.3086067 0.4082483 0 0.0000000 0.0000000 0
3 0.3872983 0.0000000 0.3535534 0.3872983 0 0.0000000 0.0000000 0
4 0.3333333 0.0000000 0.2981424 0.3333333 0 0.0000000 0.3333333 0
5 0.2156655 0.3409972 0.2156655 0.3735437 0 0.3409972 0.0000000 0
6 0.3535534 0.3227486 0.2500000 0.2886751 0 0.3535534 0.0000000 0
Scorautu Trifprat Trifrepe Vicilath Bracruta Callcusp
1 0.0000000 0.0000000 0.0000000 0 0.0000000 0
2 0.3450328 0.0000000 0.3450328 0 0.0000000 0
3 0.2236068 0.0000000 0.2236068 0 0.2236068 0
4 0.2108185 0.0000000 0.1490712 0 0.2108185 0
5 0.2641353 0.2156655 0.2156655 0 0.2156655 0
6 0.2500000 0.3227486 0.3227486 0 0.3535534 0
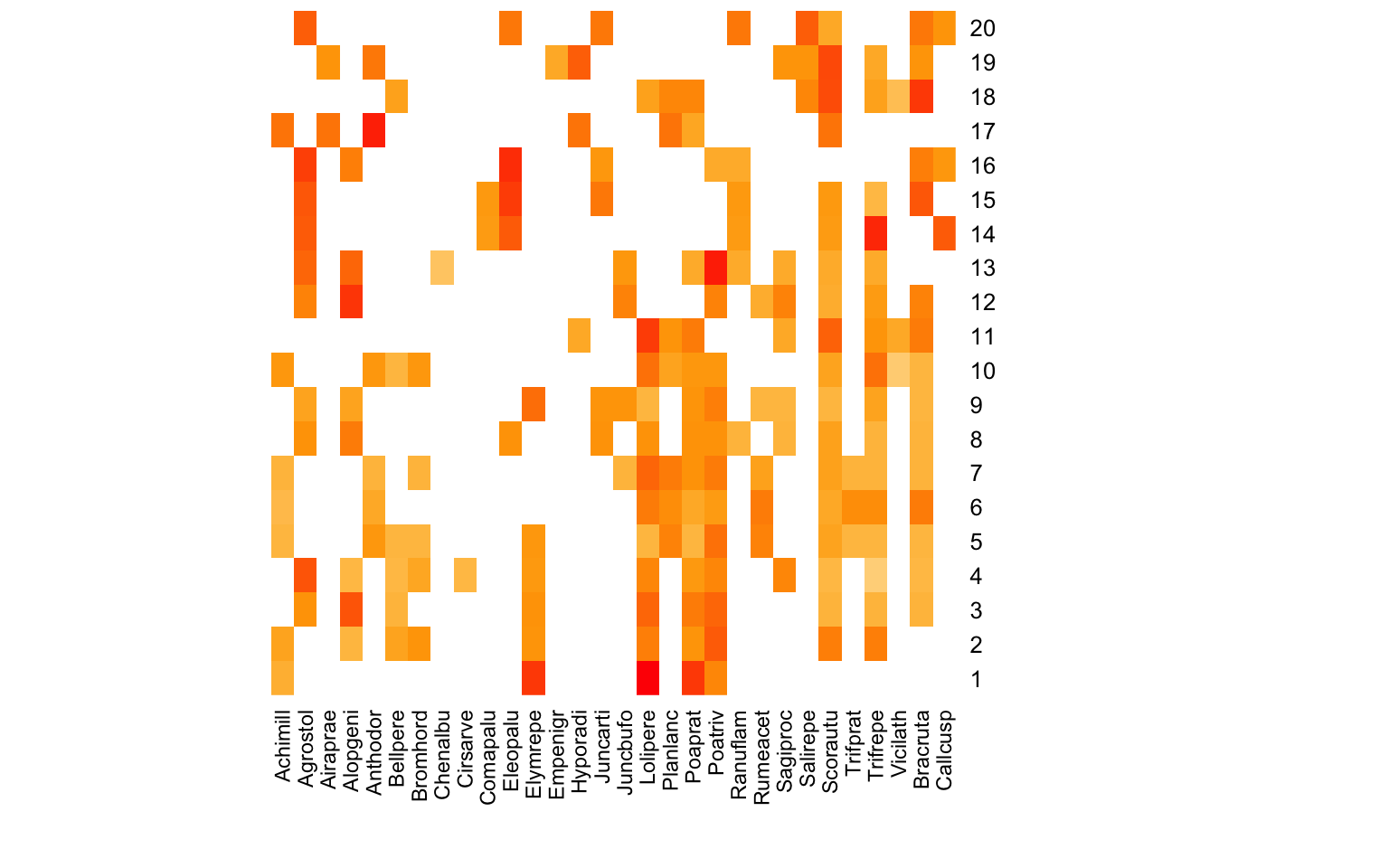
Avant de calculer les distances, sachez qu’il est courant de réaliser une heatmap pour visualiser la composition des communautés. La couleur reflète la proportion relative de l’abondance des espèces par site. Ainsi, la communauté du site 18 a une plus grande représentation de l’espèce Bracruta que de l’espèce Vicilath.
heatmap(
as.matrix(dune_hell),
Rowv = NA,
Colv = NA,
scale = "none",
col = colorRampPalette(c("white", "orange", "red"))(100),
margins = c(6, 6)
)
Calculons maintenant les distances euclidiennes sur les abondances…
hell_dist <- dist(hell_matrix, method = "euclidean")
dist_matrix <- as.matrix(hell_dist)
round(hell_dist,2) # visualiser le bas du triangle des distances
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
2 0.77
3 0.79 0.63
4 0.89 0.72 0.54
5 0.94 0.73 0.89 0.91
6 1.02 0.93 0.95 1.04 0.51
7 0.94 0.81 0.94 0.96 0.49 0.39
8 1.05 0.91 0.68 0.74 1.07 1.00 0.99
9 0.92 0.83 0.63 0.68 0.90 0.95 0.89 0.68
10 0.95 0.63 0.88 0.90 0.60 0.66 0.55 0.98 1.01
11 1.04 0.99 0.96 0.95 0.97 0.81 0.83 0.93 0.99 0.78
12 1.33 1.07 0.86 0.86 1.09 1.04 1.03 0.82 0.68 1.14 1.11
13 1.19 0.95 0.79 0.82 1.13 1.14 1.05 0.73 0.73 1.10 1.17 0.62
14 1.41 1.21 1.18 1.18 1.28 1.24 1.27 0.99 1.18 1.21 1.21 1.14 1.07
15 1.41 1.29 1.15 1.13 1.25 1.19 1.25 0.80 1.06 1.23 1.16 1.08 1.13 0.75
16 1.35 1.28 1.03 1.07 1.29 1.27 1.29 0.73 1.03 1.30 1.32 0.98 1.00 0.91 0.71
17 1.26 1.18 1.29 1.30 0.99 1.02 0.99 1.28 1.30 0.96 1.06 1.35 1.30 1.34 1.34
18 1.16 0.99 0.95 1.02 0.92 0.84 0.88 1.02 1.07 0.78 0.61 1.15 1.22 1.22 1.11
19 1.41 1.23 1.25 1.18 1.14 1.10 1.16 1.17 1.18 1.11 0.96 1.10 1.23 1.22 1.17
20 1.41 1.35 1.21 1.18 1.31 1.27 1.30 0.91 1.14 1.31 1.24 1.17 1.18 0.88 0.64
16 17 18 19
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17 1.41
18 1.29 1.13
19 1.34 0.89 0.99
20 0.67 1.35 1.08 1.14
Il faut se l’admettre : les résultats sous forme de tableau ne sont pas très intéressants. Il est préférable de combiner les distances avec une représentation visuelle pour leur donner un sens. Ici, je vous montre le clustering via un dendrogramme.
hc <- hclust(hell_dist, method = "average")
# Plot dendrogram
plot(hc, main = "Cluster des sites ~ Distances Hellinger",
xlab = "Sites", sub = "")
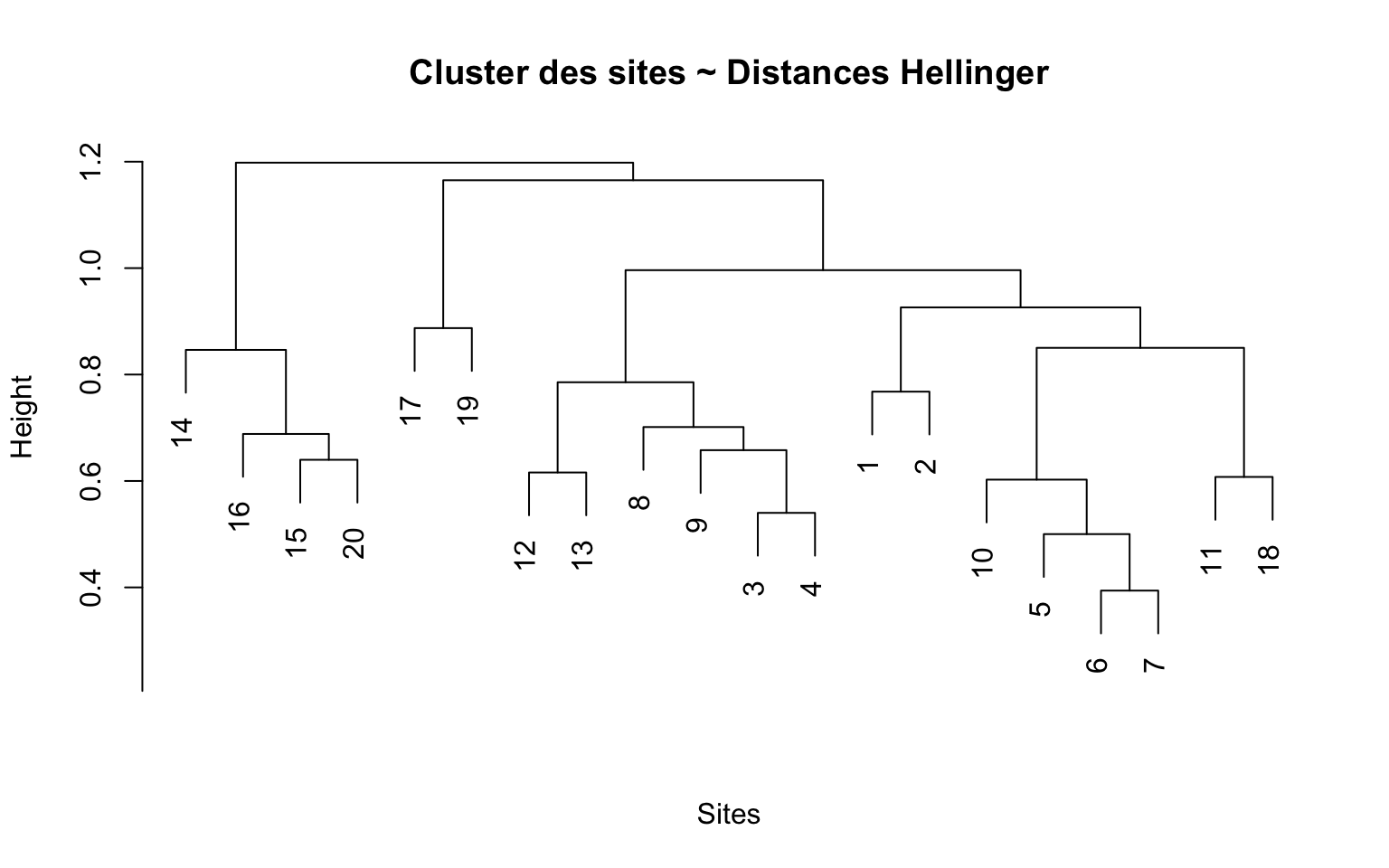
La hauteur (axe y) représente la distance, et les clusters correspondent à des regroupements de sites selon leur similarité, basée sur la distance.
Bloc D : La distance dans un espace ACP/PCA
Il est possible de calculer la distance entre nos points dans un espace ACP. Les ACP maximisent la variation des points pour établir les axes. L’ACP effectue une rotation des nuages de points, ce qui change leurs coordonnées mais n’en modifie pas les distances. L’intérêt d’une PCA est de pouvoir simplifier l’interprétation en fonction de ce qui cause le plus de variation dans notre système. L’intérêt de calculer les distances euclidiennes dans un espace PCA est de comparer la distance dans un espace simplifié par rapport à l’entièreté de notre jeu de données.
Pour ce bloc, il serait plus intéressant d’utiliser les données DUNE, mais pour compléter la formation, nous allons plutôt utiliser la base de données environnementale, DUNE.ENV, pour vous montrer comment préparer deux formats de variables catégoriques afin de calculer les distances.
Étape 1 - préparer les données
data(dune.env) # disponible avec la librarie vegan activé dans le bloc précédent
str(dune.env)
'data.frame': 20 obs. of 5 variables:
$ A1 : num 2.8 3.5 4.3 4.2 6.3 4.3 2.8 4.2 3.7 3.3 ...
$ Moisture : Ord.factor w/ 4 levels "1"<"2"<"4"<"5": 1 1 2 2 1 1 1 4 3 2 ...
$ Management: Factor w/ 4 levels "BF","HF","NM",..: 4 1 4 4 2 2 2 2 2 1 ...
$ Use : Ord.factor w/ 3 levels "Hayfield"<"Haypastu"<..: 2 2 2 2 1 2 3 3 1 1 ...
$ Manure : Ord.factor w/ 5 levels "0"<"1"<"2"<"3"<..: 5 3 5 5 3 3 4 4 2 2 ...
Rappelez-vous que nous avons besoin de données numériques pour établir nos coordonnées. Ici, les données environnementales de DUNE.ENV sont catégoriques. Il faut donc appliquer les transformations appropriées. On commence par les trois variables catégoriques qui représentent un gradient : l’humidité, la fertilisation et l’utilisation du sol. Ces variables représentent un gradient via “Ord. factor” et par les niveaux “1 < 2 < 3 < …“. On peut donc simplement utiliser la fonction as.numeric().
dune_env <- dune.env %>%
mutate(across(c(Use, Moisture, Manure), as.numeric))
La variable Management, par contre, est de nature factor et ne représente pas un gradient. Il faut donc utiliser une autre méthode, le dummy-encoding ou le one-hot method, pour la rendre numérique.
library(fastDummies) # librarie pour le codage DUMMY des variables catégoriques
dune_env <- dummy_cols(
dune_env,
select_columns = "Management",
remove_first_dummy = FALSE, # ici on veut garder tous les niveaux
remove_selected_columns = TRUE) # ici on enlève la colone d'origine
head(dune_env)
A1 Moisture Use Manure Management_BF Management_HF Management_NM
1 2.8 1 2 5 0 0 0
2 3.5 1 2 3 1 0 0
3 4.3 2 2 5 0 0 0
4 4.2 2 2 5 0 0 0
5 6.3 1 1 3 0 1 0
6 4.3 1 2 3 0 1 0
Management_SF
1 1
2 0
3 1
4 1
5 0
6 0
Cette méthode crée une nouvelle colonne de type 0/1 pour chaque niveau. Nous disposons maintenant d’une base de données numérique utilisable pour le calcul des distances.
Étape 2 : Centrer-Réduire Puisque la variable Management est maintenant représentée par quatre colonnes, il est important de centrer-réduire notre base de données, sans quoi cette variable aurait plus d’influence sur les distances.
env_scaled <- scale(dune_env)
Étape 3 : Calculer les distances sur les données “brutes”
raw_dist <- dist(env_scaled, method = "euclidean") # le calcul des distances
raw_matrix <- as.matrix(raw_dist) # préparer une matrice des distances
round(raw_matrix, 2) # visualiser la matrice des distances
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
1 0.00 3.73 1.02 0.99 3.95 3.45 3.41 4.15 4.22 4.28 4.22 2.45 2.79 5.66 6.12
2 3.73 0.00 3.81 3.80 3.97 3.56 3.83 4.46 4.11 1.63 1.44 3.92 4.35 5.26 5.70
3 1.02 3.81 0.00 0.05 3.80 3.46 3.56 3.74 3.99 4.23 4.29 1.69 1.84 5.05 5.44
4 0.99 3.80 0.05 0.00 3.81 3.46 3.56 3.74 3.99 4.23 4.28 1.71 1.86 5.07 5.46
5 3.95 3.97 3.80 3.81 0.00 1.57 3.08 3.61 2.05 3.93 4.59 3.68 4.11 4.99 4.89
6 3.45 3.56 3.46 3.46 1.57 0.00 1.59 2.69 2.11 3.92 3.84 3.52 3.98 4.85 5.25
7 3.41 3.83 3.56 3.56 3.08 1.59 0.00 2.37 3.28 4.63 3.80 3.98 4.31 5.27 6.04
8 4.15 4.46 3.74 3.74 3.61 2.69 2.37 0.00 2.98 4.82 4.43 3.57 3.45 4.38 5.15
9 4.22 4.11 3.99 3.99 2.05 2.11 3.28 2.98 0.00 3.62 4.61 3.55 3.84 4.86 5.00
10 4.28 1.63 4.23 4.23 3.93 3.92 4.63 4.82 3.62 0.00 2.65 3.99 4.39 5.36 5.52
11 4.22 1.44 4.29 4.28 4.59 3.84 3.80 4.43 4.61 2.65 0.00 4.18 4.68 4.97 5.72
12 2.45 3.92 1.69 1.71 3.68 3.52 3.98 3.57 3.55 3.99 4.18 0.00 1.02 3.95 4.28
13 2.79 4.35 1.84 1.86 4.11 3.98 4.31 3.45 3.84 4.39 4.68 1.02 0.00 4.13 4.42
14 5.66 5.26 5.05 5.07 4.99 4.85 5.27 4.38 4.86 5.36 4.97 3.95 4.13 0.00 1.62
15 6.12 5.70 5.44 5.46 4.89 5.25 6.04 5.15 5.00 5.52 5.72 4.28 4.42 1.62 0.00
16 3.00 4.50 2.19 2.20 4.66 4.15 4.07 3.17 4.39 4.87 4.47 1.63 1.28 3.98 4.67
17 4.34 4.00 4.24 4.24 3.62 3.69 4.58 4.74 3.26 3.54 4.42 3.71 4.23 3.83 3.97
18 4.32 3.96 4.31 4.31 3.47 3.61 4.56 5.03 3.54 3.66 4.37 3.88 4.51 4.04 4.10
19 4.83 4.54 4.51 4.51 4.25 4.28 5.05 4.49 3.26 3.84 4.91 3.74 3.98 3.61 3.80
20 4.82 4.54 4.51 4.51 4.27 4.28 5.04 4.50 3.26 3.84 4.91 3.76 4.01 3.68 3.88
16 17 18 19 20
1 3.00 4.34 4.32 4.83 4.82
2 4.50 4.00 3.96 4.54 4.54
3 2.19 4.24 4.31 4.51 4.51
4 2.20 4.24 4.31 4.51 4.51
5 4.66 3.62 3.47 4.25 4.27
6 4.15 3.69 3.61 4.28 4.28
7 4.07 4.58 4.56 5.05 5.04
8 3.17 4.74 5.03 4.49 4.50
9 4.39 3.26 3.54 3.26 3.26
10 4.87 3.54 3.66 3.84 3.84
11 4.47 4.42 4.37 4.91 4.91
12 1.63 3.71 3.88 3.74 3.76
13 1.28 4.23 4.51 3.98 4.01
14 3.98 3.83 4.04 3.61 3.68
15 4.67 3.97 4.10 3.80 3.88
16 0.00 4.74 5.00 4.52 4.54
17 4.74 0.00 0.81 1.52 1.54
18 5.00 0.81 0.00 2.32 2.33
19 4.52 1.52 2.32 0.00 0.09
20 4.54 1.54 2.33 0.09 0.00
Étape 4 : Réaliser une ACP
env_PCA <- prcomp(env_scaled, center = FALSE, scale. = FALSE)
summary(env_PCA)
Importance of components:
PC1 PC2 PC3 PC4 PC5 PC6 PC7
Standard deviation 1.6549 1.3886 1.1399 1.0227 0.71027 0.64156 0.26770
Proportion of Variance 0.3423 0.2410 0.1624 0.1307 0.06306 0.05145 0.00896
Cumulative Proportion 0.3423 0.5834 0.7458 0.8765 0.93959 0.99104 1.00000
PC8
Standard deviation 1.943e-16
Proportion of Variance 0.000e+00
Cumulative Proportion 1.000e+00
Étape 5 : Extraire les coordonnées des points de l’ACP (les scores)
pca_scores <- as.data.frame(env_PCA$x) # extrait les coordonnées
pca_scores$site <- rownames(pca_scores) # extrait le nom des sites
Étape 6 : Réaliser le graphique de l’ACP pour visualiser la distribution des sites en fonction des quatre variables environnementales.
ggplot(pca_scores, aes(PC1, PC2, label = site)) +
geom_point(size = 5, color = "#008080") +
geom_text(vjust = -1, size = 8) +
theme_minimal()
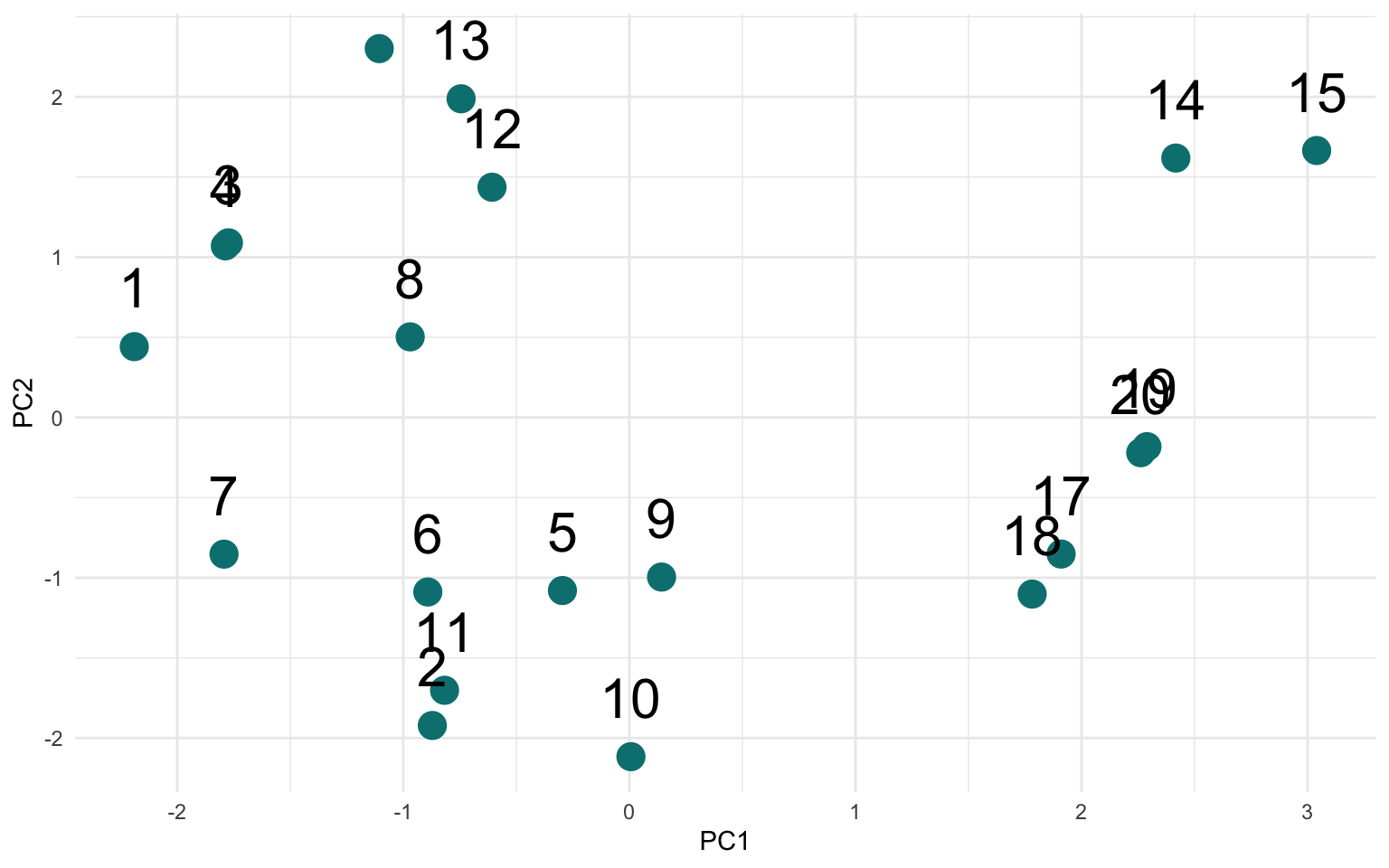
Étape 7 : Préparer la matrice des distances euclidiennes des deux premiers axes de l’ACP
pca_dist <- dist(pca_scores[, c("PC1", "PC2")], method = "euclidean") # calculer la distance des points en fonction des 2 premiers axes seulement
pca_matrix <- as.matrix(pca_dist) # prépare la matrice
round(pca_matrix, 2) # affiche les distances de la matrice ACP
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
1 0.00 2.71 0.77 0.75 2.43 2.01 1.35 1.22 2.74 3.37 2.55 1.87 2.12 4.75 5.37
2 2.71 0.00 3.14 3.13 1.02 0.83 1.41 2.43 1.37 0.90 0.23 3.37 3.91 4.83 5.31
3 0.77 3.14 0.00 0.02 2.62 2.35 1.94 1.00 2.83 3.67 2.95 1.22 1.37 4.22 4.85
4 0.75 3.13 0.02 0.00 2.62 2.34 1.92 1.00 2.83 3.66 2.94 1.24 1.39 4.24 4.86
5 2.43 1.02 2.62 2.62 0.00 0.60 1.51 1.72 0.45 1.08 0.81 2.54 3.10 3.83 4.32
6 2.01 0.83 2.35 2.34 0.60 0.00 0.93 1.59 1.04 1.36 0.62 2.54 3.08 4.27 4.80
7 1.35 1.41 1.94 1.92 1.51 0.93 0.00 1.59 1.94 2.20 1.29 2.58 3.03 4.88 5.45
8 1.22 2.43 1.00 1.00 1.72 1.59 1.59 0.00 1.87 2.79 2.21 1.00 1.50 3.57 4.17
9 2.74 1.37 2.83 2.83 0.45 1.04 1.94 1.87 0.00 1.13 1.19 2.54 3.11 3.47 3.93
10 3.37 0.90 3.67 3.66 1.08 1.36 2.20 2.79 1.13 0.00 0.92 3.61 4.17 4.44 4.85
11 2.55 0.23 2.95 2.94 0.81 0.62 1.29 2.21 1.19 0.92 0.00 3.15 3.69 4.64 5.12
12 1.87 3.37 1.22 1.24 2.54 2.54 2.58 1.00 2.54 3.61 3.15 0.00 0.57 3.03 3.65
13 2.12 3.91 1.37 1.39 3.10 3.08 3.03 1.50 3.11 4.17 3.69 0.57 0.00 3.18 3.80
14 4.75 4.83 4.22 4.24 3.83 4.27 4.88 3.57 3.47 4.44 4.64 3.03 3.18 0.00 0.62
15 5.37 5.31 4.85 4.86 4.32 4.80 5.45 4.17 3.93 4.85 5.12 3.65 3.80 0.62 0.00
16 2.15 4.23 1.38 1.41 3.48 3.40 3.23 1.80 3.53 4.56 4.01 1.00 0.48 3.59 4.19
17 4.30 2.98 4.16 4.17 2.22 2.81 3.70 3.18 1.77 2.28 2.86 3.40 3.89 2.52 2.76
18 4.26 2.78 4.18 4.18 2.08 2.67 3.58 3.18 1.64 2.04 2.67 3.49 3.99 2.79 3.04
19 4.52 3.61 4.26 4.26 2.74 3.31 4.14 3.33 2.30 2.99 3.46 3.32 3.73 1.80 1.99
20 4.50 3.57 4.24 4.25 2.70 3.27 4.10 3.31 2.26 2.95 3.42 3.31 3.73 1.84 2.04
16 17 18 19 20
1 2.15 4.30 4.26 4.52 4.50
2 4.23 2.98 2.78 3.61 3.57
3 1.38 4.16 4.18 4.26 4.24
4 1.41 4.17 4.18 4.26 4.25
5 3.48 2.22 2.08 2.74 2.70
6 3.40 2.81 2.67 3.31 3.27
7 3.23 3.70 3.58 4.14 4.10
8 1.80 3.18 3.18 3.33 3.31
9 3.53 1.77 1.64 2.30 2.26
10 4.56 2.28 2.04 2.99 2.95
11 4.01 2.86 2.67 3.46 3.42
12 1.00 3.40 3.49 3.32 3.31
13 0.48 3.89 3.99 3.73 3.73
14 3.59 2.52 2.79 1.80 1.84
15 4.19 2.76 3.04 1.99 2.04
16 0.00 4.36 4.46 4.21 4.21
17 4.36 0.00 0.28 0.77 0.72
18 4.46 0.28 0.00 1.05 1.00
19 4.21 0.77 1.05 0.00 0.05
20 4.21 0.72 1.00 0.05 0.00
Étape 8 : Affiher un graphique qui compare les distances brutes des distances des deux premiers axes de l’ACP
comparison <- data.frame(
raw_space = as.vector(raw_matrix),
PCA_space = as.vector(pca_matrix)
)
ggplot(comparison, aes(raw_space, PCA_space)) +
geom_point(size = 3, alpha = 0.6) +
geom_abline(slope = 1, intercept = 0, color = "red") + # 1:1 line
theme_minimal() +
labs(title = "Raw vs PCA Distances in Environmental Space",
x = "Distance in raw environmental space",
y = "Distance in PCA space")
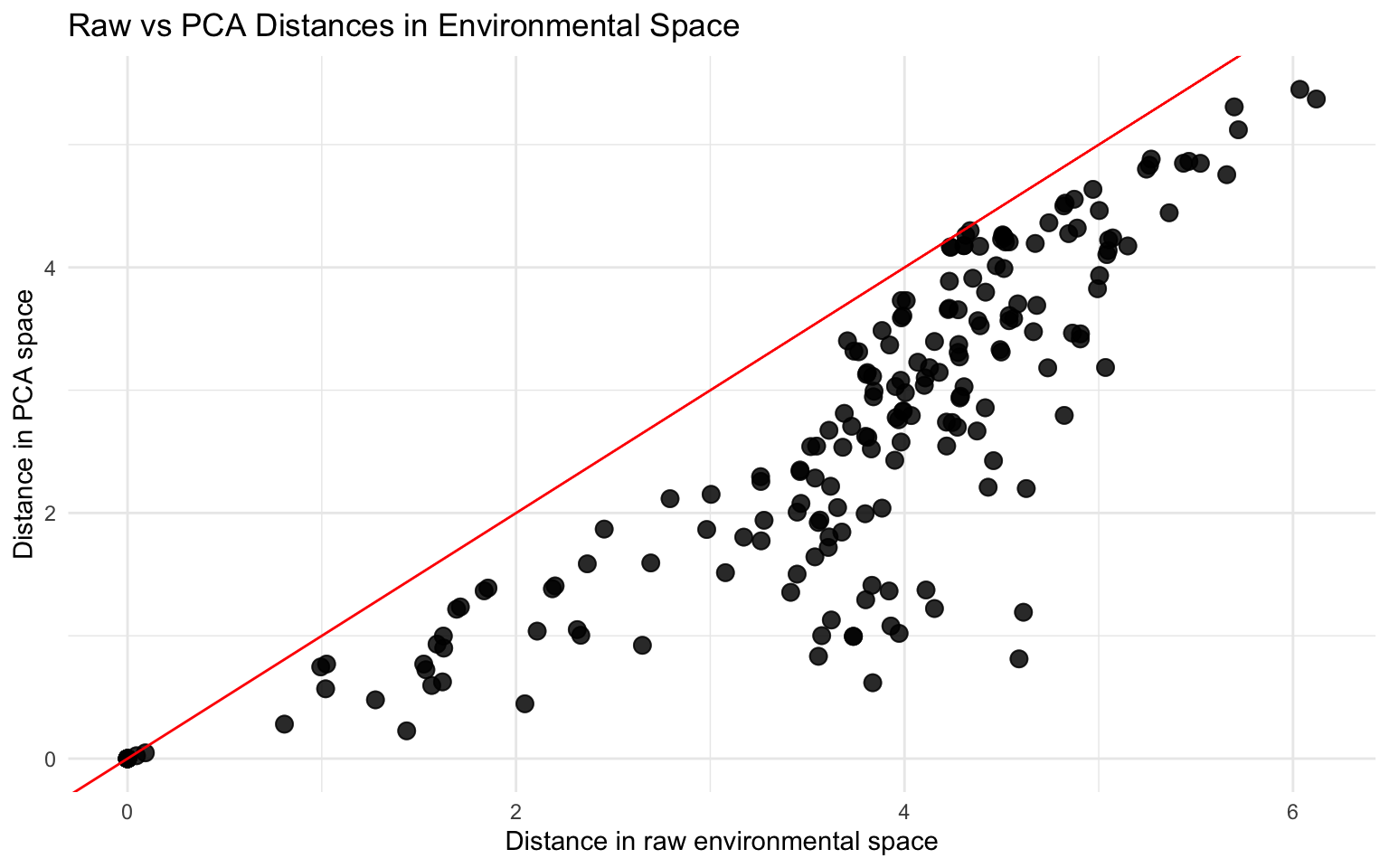
On voit ici que les points sont tous en dessous de la ligne 1:1. Cela signifie que les distances dans l’espace ACP surestiment la similarité.
Et si l’on conservait un axe supplémentaire ?
pca_dist <- dist(pca_scores[, c("PC1", "PC2", "PC3")], method = "euclidean")
pca_matrix <- as.matrix(pca_dist)
round(pca_matrix, 2)
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15
1 0.00 2.80 0.78 0.76 3.47 3.18 2.85 3.00 3.66 3.47 2.63 1.88 2.14 4.87 5.47
2 2.80 0.00 3.26 3.24 3.35 3.30 3.53 4.23 3.43 0.90 0.24 3.49 4.04 5.14 5.59
3 0.78 3.26 0.00 0.02 3.52 3.32 3.08 2.80 3.64 3.78 3.05 1.22 1.38 4.32 4.93
4 0.76 3.24 0.02 0.00 3.52 3.31 3.07 2.80 3.64 3.77 3.04 1.24 1.40 4.34 4.95
5 3.47 3.35 3.52 3.52 0.00 0.60 1.51 1.74 0.45 3.45 3.22 3.40 3.79 4.09 4.55
6 3.18 3.30 3.32 3.31 0.60 0.00 0.93 1.62 1.04 3.54 3.18 3.40 3.77 4.51 5.01
7 2.85 3.53 3.08 3.07 1.51 0.93 0.00 1.60 1.94 3.98 3.41 3.46 3.75 5.10 5.64
8 3.00 4.23 2.80 2.80 1.74 1.62 1.60 0.00 1.89 4.51 4.04 2.72 2.87 3.95 4.51
9 3.66 3.43 3.64 3.64 0.45 1.04 1.94 1.89 0.00 3.41 3.29 3.37 3.77 3.73 4.17
10 3.47 0.90 3.78 3.77 3.45 3.54 3.98 4.51 3.41 0.00 0.94 3.74 4.31 4.81 5.19
11 2.63 0.24 3.05 3.04 3.22 3.18 3.41 4.04 3.29 0.94 0.00 3.26 3.81 4.93 5.39
12 1.88 3.49 1.22 1.24 3.40 3.40 3.46 2.72 3.37 3.74 3.26 0.00 0.57 3.14 3.75
13 2.14 4.04 1.38 1.40 3.79 3.77 3.75 2.87 3.77 4.31 3.81 0.57 0.00 3.27 3.87
14 4.87 5.14 4.32 4.34 4.09 4.51 5.10 3.95 3.73 4.81 4.93 3.14 3.27 0.00 0.62
15 5.47 5.59 4.93 4.95 4.55 5.01 5.64 4.51 4.17 5.19 5.39 3.75 3.87 0.62 0.00
16 2.19 4.37 1.41 1.43 4.06 3.99 3.87 2.97 4.07 4.71 4.14 1.01 0.49 3.65 4.25
17 4.32 3.21 4.18 4.18 2.99 3.45 4.23 3.91 2.64 2.61 3.06 3.41 3.89 2.59 2.82
18 4.28 3.01 4.19 4.19 2.91 3.36 4.14 3.93 2.57 2.39 2.88 3.49 3.99 2.86 3.10
19 4.56 3.83 4.28 4.29 3.35 3.82 4.58 3.99 2.96 3.28 3.66 3.34 3.74 1.87 2.06
20 4.53 3.78 4.26 4.27 3.32 3.80 4.55 3.98 2.94 3.24 3.62 3.33 3.74 1.91 2.10
16 17 18 19 20
1 2.19 4.32 4.28 4.56 4.53
2 4.37 3.21 3.01 3.83 3.78
3 1.41 4.18 4.19 4.28 4.26
4 1.43 4.18 4.19 4.29 4.27
5 4.06 2.99 2.91 3.35 3.32
6 3.99 3.45 3.36 3.82 3.80
7 3.87 4.23 4.14 4.58 4.55
8 2.97 3.91 3.93 3.99 3.98
9 4.07 2.64 2.57 2.96 2.94
10 4.71 2.61 2.39 3.28 3.24
11 4.14 3.06 2.88 3.66 3.62
12 1.01 3.41 3.49 3.34 3.33
13 0.49 3.89 3.99 3.74 3.74
14 3.65 2.59 2.86 1.87 1.91
15 4.25 2.82 3.10 2.06 2.10
16 0.00 4.36 4.46 4.21 4.21
17 4.36 0.00 0.28 0.78 0.73
18 4.46 0.28 0.00 1.06 1.01
19 4.21 0.78 1.06 0.00 0.05
20 4.21 0.73 1.01 0.05 0.00
comparison <- data.frame(
raw_space = as.vector(raw_matrix),
PCA_space = as.vector(pca_matrix)
)
ggplot(comparison, aes(raw_space, PCA_space)) +
geom_point(size = 3, alpha = 0.6) +
geom_abline(slope = 1, intercept = 0, color = "red") + # 1:1 line
theme_minimal() +
labs(title = "Raw vs PCA Distances in Environmental Space",
x = "Distance in raw environmental space",
y = "Distance in PCA space")
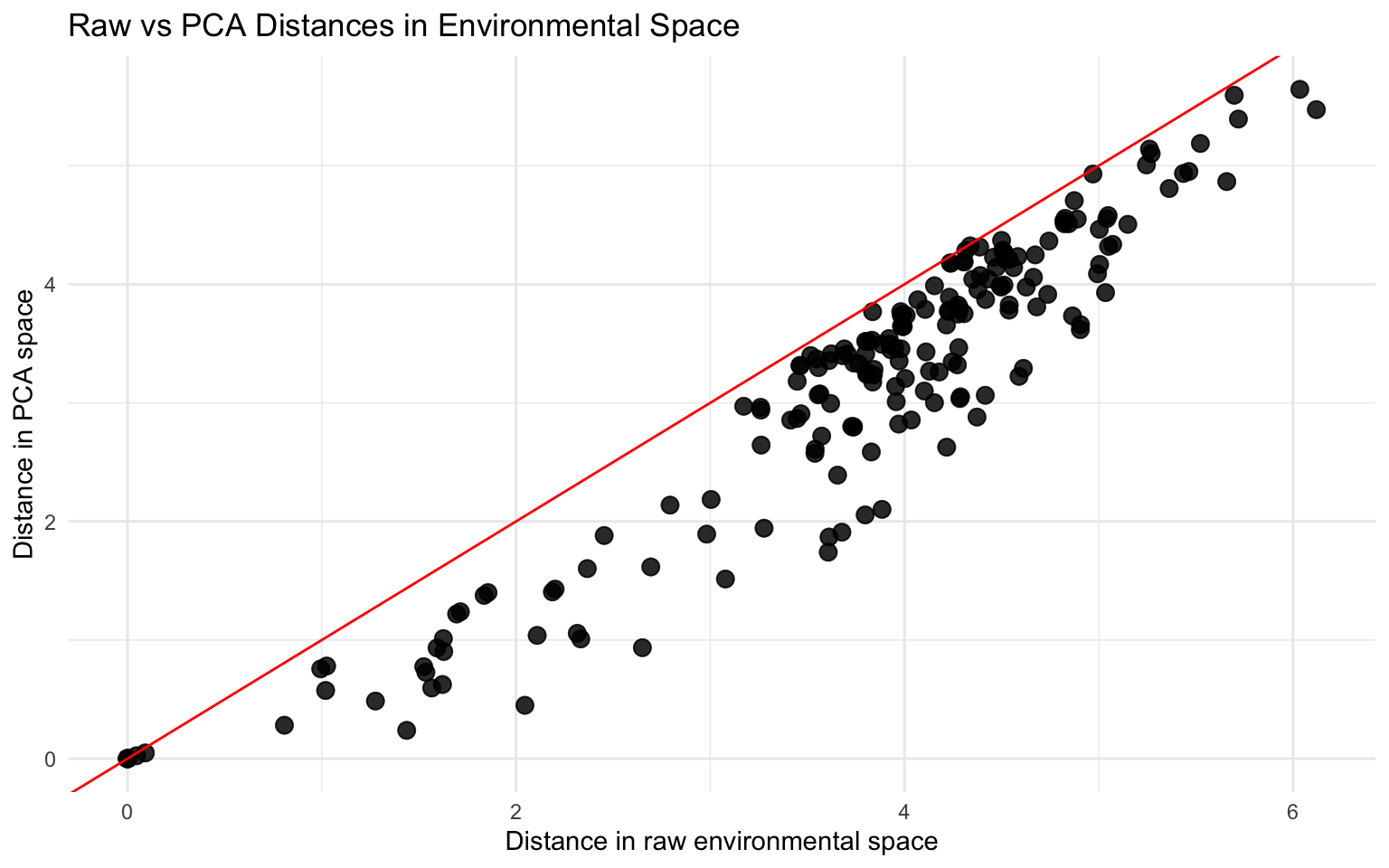
Les points sont légèrement plus près de la ligne. Plus on garde d’axes, plus les points se rapprochent de la ligne 1:1. Comparer les distances euclidiennes par rapport aux distances brutes est un indicateur de l’information que l’on perd volontairement lorsque l’on choisit le nombre d’axes à conserver pour simplifier l’interprétation via une ACP.
Conclusion
Dès lors que vous êtes capable de décrire vos points à l’aide de coordonnées numériques, les distances euclidiennes peuvent être calculées sur quasiment n’importe quelle donnée. C’est une analyse qui permet de mesurer la similarité ou la dissimilarité entre vos points. Le défi consiste à bien définir vos points et les variables qui les décrivent : on peut utiliser le même jeu de données pour répondre à plusieurs questions écologiques.
En sus
Sachez qu’il existe différents packages spécialisés pour calculer les distances dans certaines circonstances. Par exemple, philentropy() permets d’interchanger entre différentes distances de la famille Minowski (Euclidiennes, Manhattan, Minowski, etc.) ainsi que différentes probabilités de distribution (Bray-Curtis, Jaccard, Hellinger, Chi-squared, etc.). Ce package est optimal pour les grosses matrices et les données compositionnelles. Le package nnspat() est spécialisé pour calculer les distances spatiales dites “voisin le plus proche”, très utiles en Géo statistiques. En gros, il permet d’intégrer l’influence des points à proximité dans le calcul. Sachez que pour l’analyse d’un cours d’eau, spécifiquement pour la distance entre des points le long de son écoulement upstream-downstream, soit les packages SSN ou le SSN2.