Fonctions and itération

Charles Martin

Février 2020

Introduction

Les fonctions permettent d’automatiser des choses plutôt que de copier-coller.

3 avantages majeurs :

Quand écrire une fonction?

Une bonne pratique est de penser à écrire une fonction au moment où on copie-colle du code pour la 2e fois (i.e. on en a maintenant 3 copies)

Par exemple, si on a l’abondance relative des espèces dans 3 communautés

com1 = c(0.5,0.3,0.2)
com2 = c(0.7,0.2,0.1,0.1)
com3 = c(0.9,0.1)

On pourrait calculer la diversité de Shannon pour la première comme ceci :

-sum(com1*log(com1))

[1] 1.029653

Ensuite la deuxième et la troisième

-sum(com2*log(com2))

[1] 1.032077

-sum(com3*log(com3))

[1] 0.325083

On a copié-collé 2 fois, il est temps d’écrire une fonction…

Une bonne première étape pour écrire une fonction est de déterminer de quoi la fonction a besoin, quelles sont ses entrées. Ici, ce sont les abondances relatives dans la communautés. Appelons-les p, comme dans la formule traditionnelle

p <- com1
-sum(p*log(p))

[1] 1.029653

p <- com2
-sum(p*log(p))

[1] 1.032077

Remarquez que je teste immédiatement mon code, pour m’assurer que j’ai extrait tout ce dont il avait besoin pour fonctionner

Ensuite, il ne reste qu’à emballer ce code et à indiquer à R que notre code nécessite un seul argument, soit p

Si on ne mentionne rien, une fonction renvoie le résultat de la dernière commande exécutée.

diversite_shannon <- function(p) {
  -sum(p*log(p))
}
diversite_shannon(com1)

[1] 1.029653

diversite_shannon(com2)

[1] 1.032077

diversite_shannon(com3)

[1] 0.325083

Notre code est maintenant beaucoup lisible ET facile d’entretien

(oui, nous avons encore du copier-coller…)

Exécution conditionnelle

On peut insérer des conditions à l’intérieur de nos fonctions (partout en fait), à l’aide du mot-clé if

La structure d’un IF se définit comme ceci :

if (condition) {
  # s'exécute si c'est vrai
} else {
  # s'exécute si c'est faux
}

salutations <- function(nom) {
  if (nom == "Charles") {
   print("Allo Charles")
  } else {
    print("Qui êtes vous?")
  }
}
salutations("Esteban")

[1] "Qui êtes vous?"

salutations("Charles")

[1] "Allo Charles"

Remarquez qu’il n’est pas nécessaire de retourner une valeur ou de travailler avec cette valeur de retour.

Les arguments

Les fonctions peuvent posséder autant d’arguments que l’on désire

Habituellement, dans R, les premiers arguments contiennent les données, et les derniers détails sur comme faire le calcul.

Les arguments concernant les détails du calcul peuvent avoir des valeurs par défaut

pile_face <- function(n,probabilite_pile = 0.5) {
  sample(
    c("pile","face"),
    size = n, 
    prob = c(probabilite_pile,1 - probabilite_pile),
    replace = TRUE
  )
}
pile_face(25)

 [1] "face" "face" "face" "face" "face" "pile" "pile" "pile" "face" "face"
[11] "pile" "face" "pile" "pile" "pile" "face" "face" "pile" "face" "face"
[21] "pile" "pile" "pile" "face" "face"

pile_face(25, 0.9)

 [1] "pile" "pile" "pile" "pile" "pile" "pile" "pile" "pile" "pile" "pile"
[11] "pile" "pile" "pile" "pile" "face" "pile" "pile" "pile" "pile" "pile"
[21] "pile" "pile" "pile" "face" "pile"

Vérification des valeurs passées aux arguments

Lorsque l’on devient confortable avec l’écriture de fonction et qu’on en utilise beaucoup, on arrive rapidement un point où ne se rappelle plus le détail du code à l’intérieur de chaque fonction et ses contraintes associées.

Par exemple, notre fonction de diversité de Shannon s’attend à recevoir les probabilités relatives, le calcul n’est pas défini si la somme des p n’est pas 1.

Pourtant notre fonction nous laisse faire le calcul, même sur des abondances absolues

diversite_shannon(c(1,5,25,12))

[1] -118.338

Pour se protéger contre notre futur-nous, on peut inclure des vérifications, qui arrêtent la fonction si les conditions ne sont pas respectées…

diversite_shannon <- function(p) {
  stopifnot(sum(p) == 1)
  - sum(p*log(p))
}
diversite_shannon(c(1,5,25,12))

Error in diversite_shannon(c(1, 5, 25, 12)): sum(p) == 1 is not TRUE

On peut aussi écrire des messages d’erreur plus user-friendly, avec un petit plus de code…

diversite_shannon <- function(p) {
  if (sum(p) != 1) {
    stop("L'argument p doit contenir des probabilités relatives, dont la somme est 1.")
  }
  - sum(p*log(p))
}
diversite_shannon(c(1,5,25,12))

Error in diversite_shannon(c(1, 5, 25, 12)): L'argument p doit contenir des probabilités relatives, dont la somme est 1.

L’argument spécial dot-dot-dot (…)

Les fonctions R peuvent contenir un argument spécial nommé dot-dot-dot. Cet argument, s’il est présent, attrape tous les arguments qui ne sont pas attrapés par des noms.

Il peut être très pratique, entre autres, pour passer des arguments aux fonctions suivantes.

Si par exemple chaque fois que l’on fait un histogramme on lui remet les mêmes couleurs, on pourrait se créer notre propre fonction, qui appelle l’originale avec nos arguments préférés :

bleustogram <- function(...){
  hist(..., col = "royalblue")
}
bleustogram(rnorm(50))


bleustogram(rlnorm(100))

Plusieurs points de retour

Une fonction R peut contenir plusieurs points où elle s’arrête pour retourner une valeur. Il faut alors nommer ces points explicitement…

diversite <- function(p, indice = "shannon") {
  if (indice == "shannon") {
    return(-sum(p*log(p)))
  } else if (indice == "simpson") {
    return(sum(p^2))
  } else {
    stop("L'indice doit être shannon ou simpson")
  }
}
diversite(c(0.5,0.3,0.2))

[1] 1.029653

diversite(c(0.5,0.3,0.2), indice = "simpson")

[1] 0.38

Notes à propos de l’environnement

Tout ce qui est créé à l’intérieur d’une fonction n’existe que dans la fonction, et n’est pas accessible de l’extérieur. Les objets sont remis à zéro chaque fois que la fonction est appelée.

Par contre, une des particularités de R est que si une variable n’est pas définie à l’intérieur d’une fonction, R va aussi chercher à l’extérieur, dans l’environnement global pour voir si elle existe.

b <- 2
f1 <- function(d) {
  d * b
}
f1(3)

[1] 6

f2 <- function(d) {
  b <- 8
  d * b
}
f2(3)

[1] 24

b

[1] 2

d

Error in eval(expr, envir, enclos): object 'd' not found

C’est pourquoi il faut être très prudent lorsque l’on extrait les arguments nécessaires à une fonction et qu’il est très important de redémarrer notre session de R de temps à autre, pour être certain qu’il n’y a pas une variable avec un nom dérangeant qui survivrait dans notre environnement de travail

Introduction à l’itération

Outre l’utilisation de fonctions, une autre technique pour réduire la duplication dans votre code (et donc les bug et le copier-coller) se nomme l’itération (syn. répétition)

Il existe deux styles d’itération principaux dans R : la programmation impérative et la programmation fonctionnelle.

La programmation impérative inclut les boucles FOR et WHILE. C’est souvent la façon la plus intuitive de commencer car les concepts sont explicites.

Par contre, la programmation impérative implique beaucoup de code de plomberie qui revient d’une boucle à l’autre et qui noie l’intention réelle du code. La programmation fonctionnelle permet d’extraire le coeur du problème, et de produire du code plus dense, plus facile à lire et qui crée moins d’erreurs

Les boucles FOR

Prenons l’exemple de la chanson Baby Shark : https://genius.com/Pinkfong-baby-shark-lyrics

Si on veut automatiser l’écriture du premier couplet de la chanson, on peut écrire :

for (i in 1:3) {
  print("Baby shark, doo doo doo doo doo doo")
}
print("Baby shark!")

[1] "Baby shark, doo doo doo doo doo doo"
[1] "Baby shark, doo doo doo doo doo doo"
[1] "Baby shark, doo doo doo doo doo doo"
[1] "Baby shark!"

Une boucle FOR a 2 composantes principales : La première ligne qui définit combien de fois effectuer la boucle Le code entre {} qui définit ce que l’on veut répéter à chaque itération

Les itérations n’ont pas nécessairement besoin de faire un travail identique, elles peuvent faire chacune une action personnalisée basée sur l’indice

mots = c("Baby shark","Mommy shark","It's the end")
for (i in seq_along(mots)) { # vs. 1:length(mots)
  print(paste0(mots[i],", doo doo doo doo doo doo"))
}

[1] "Baby shark, doo doo doo doo doo doo"
[1] "Mommy shark, doo doo doo doo doo doo"
[1] "It's the end, doo doo doo doo doo doo"

Imbrication

Vous me voyez probablement venir, on peut aussi imbriquer des boucles les unes dans les autres

mots = c("Baby shark","Mommy shark","It's the end")
for (i in seq_along(mots)) {
  for (j in 1:3) {
    print(paste0(mots[i],", doo doo doo doo doo doo"))
  }
  print(paste0(mots[i],"!"))
}

[1] "Baby shark, doo doo doo doo doo doo"
[1] "Baby shark, doo doo doo doo doo doo"
[1] "Baby shark, doo doo doo doo doo doo"
[1] "Baby shark!"
[1] "Mommy shark, doo doo doo doo doo doo"
[1] "Mommy shark, doo doo doo doo doo doo"
[1] "Mommy shark, doo doo doo doo doo doo"
[1] "Mommy shark!"
[1] "It's the end, doo doo doo doo doo doo"
[1] "It's the end, doo doo doo doo doo doo"
[1] "It's the end, doo doo doo doo doo doo"
[1] "It's the end!"

Conserver un résultat pour chaque itération

On peut aussi conserver un résultat pour chacune des itérations. Auquel cas, il est fortement recommandé de pré-allouer notre objet de résultats avant de commencer. C’est la clé pour obtenir des boucles rapides dans R.

Par exemple, si on se prépare une boucle qui calcule la valeur absolue d’une série de nombres

nombres <- c(-1,0,1,-5)
valeurs_absolues <- vector("double", length(nombres))
for (i in seq_along(nombres)) {
  valeurs_absolues[i] <- abs(nombres[i])
}
valeurs_absolues

[1] 1 0 1 5

Nombre d’itération inconnu

Lorsque l’on ne sait pas d’avance combien de fois notre boucle s’effectuera, il existe une autre structure de R permettant ce type d’itération : while

Cette instruction est particulièrement pratique pour les simulations.

Par exemple, combien de tirages à pile-ou-face doit-on faire avant d’obtenir 3 pile de suite?

tirages <- 0
piles_de_suite <- 0

while (piles_de_suite < 3) {
  
  resultat <- pile_face(1)
  
  if ((resultat) == "pile") {
    piles_de_suite <- piles_de_suite + 1
  } else {
    piles_de_suite <- 0
  }
  
  tirages <- tirages + 1
}

tirages

[1] 26

La famille Map

Le concept d’itération peut être attaqué d’une manière complètement différente avec la programmation fonctionnelle. Dans R, il existe le package purrr contenant plusieurs fonctions permettant d’attaquer la programmation fonctionnelle de façon simple et intuitive.

library(purrr)

Le principe est toujours le même : plutôt que de fournir le code qui structure la boucle, on fournit à map une fonction et une série d’éléments sur lesquels appliquer cette fonction.

Il existe une série de fonctions map selon le type de résultat que l’on veut obtenir :

Si on reprend par exemple notre code sur les valeurs absolues, il pourrait être converti en ceci

nombres <- c(-1,0,1,-5)
valeurs_absolues <- map_dbl(nombres, abs)
valeurs_absolues

[1] 1 0 1 5

On s’épargne toute la plomberie sur comment faire la boucle.

On peut aussi passer une fonction que l’on crée nous-même, p. ex. si on voulait faire valeur absolue + 10

nombres <- c(-1,0,1,-5)
ma_fonction <- function(x) {
  abs(x) + 10
}
map_dbl(nombres, ma_fonction)

[1] 11 10 11 15

Si la fonction ne sera utilisée qu’à ce moment et jamais ailleurs, elle peut être définie de façon anonyme, à même l’appel à map

nombres <- c(-1,0,1,-5)
map_dbl(nombres, function(x) {abs(x) + 10})

[1] 11 10 11 15

On limite généralement ce genre d’utilisation au code plutôt court.

Les raccourcis inclus

Un des avantages des fonctions map du package purrr est qu’ils permettent de couper la partie évidente de ce code avec des raccourcis :

nombres <- c(-1,0,1,-5)
map_dbl(nombres, ~ abs(.) + 10)

[1] 11 10 11 15

On peut remplacer la partie function etc. par un ~ et le nom de la variable par un point.

Gérer les problèmes

Lorsque l’on utilise les fonctions map sur de longues séries de données, il peut arriver que notre fonction échoue pour une raison ou pour une autre. Lorsqu’un problème survient, la fonction map s’arrête, avec un message d’erreur, mais on ne récupère pas les résultats partiels construits jusque-là (contrairement aux boucles FOR)

Si on reprend par exemple notre fonction sur la diversité de Shannon, si on a une communauté erronée, on perd l’ensemble de nos résultats…

communautes <- list(
  c(0.5,0.3,0.2),
  c(0.9,0.1),
  c(10,3,1)
)

map_dbl(communautes,diversite_shannon)

Error in .f(.x[[i]], ...): L'argument p doit contenir des probabilités relatives, dont la somme est 1.

Le package purrr inclut plusieurs adverbes pour gérer ce genre de situations. Dans chaque cas, leur travail est d’emballer notre fonction en modifiant son comportement en cas d’erreur. Je vous présente uniquement le cas le plus simple, l’adverbe possibly auquel on fournit la valeur à mettre dans les sorties en cas de problèmes

map_dbl(communautes,possibly(diversite_shannon,NA))

[1] 1.029653 0.325083       NA

Il existe aussi une fonction map pour créer des tableaux de données

map_df(communautes,function(x){
  data.frame(
    richesse = length(x),
    shannon = diversite(x, indice = "shannon"),
    simpson = diversite(x, indice = "simpson")
  )
})

  richesse    shannon simpson
1        3   1.029653    0.38
2        2   0.325083    0.82
3        3 -26.321688  110.00

On peut de cette façon rassembler une série de fichiers csv dans un même tableau de données

fichiers <- list.files(
  "/Dossier/Avec/Les/Donnees",
  pattern = "*.csv",
  full.names = TRUE
)
tableau <- map_df(fichiers,read.csv)

Tableaux de données en entrée et en sortie

Mise en situation : nous avons exploré la relation entre le poids du corps et le poids du cerveau des mammifères

library(ggplot2)
library(dplyr)


Attaching package: 'dplyr'

The following objects are masked from 'package:stats':

    filter, lag

The following objects are masked from 'package:base':

    intersect, setdiff, setequal, union

data(msleep)

msleep %>% 
  ggplot(aes(x = bodywt, y = brainwt)) +
  geom_point(aes(color = vore)) +
  scale_x_log10() +
  scale_y_log10()

Warning: Removed 27 rows containing missing values (geom_point).

On voudrait maintenant rouler une régression par groupe pour comparer les paramètres

Essayons de voir comme on l’aurait fait pour un seul groupe :

x <- msleep %>% filter(vore == "herbi")
m <- lm(log(brainwt)~log(bodywt),data = x)
summary(m)


Call:
lm(formula = log(brainwt) ~ log(bodywt), data = x)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.79504 -0.28970 -0.08648  0.19723  1.12209 

Coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) -4.94213    0.12464  -39.65  < 2e-16 ***
log(bodywt)  0.74212    0.03007   24.68 2.48e-15 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.4864 on 18 degrees of freedom
  (12 observations deleted due to missingness)
Multiple R-squared:  0.9713,	Adjusted R-squared:  0.9697 
F-statistic: 609.1 on 1 and 18 DF,  p-value: 2.484e-15

Si on veut aller récupérer ces chiffres pour les mettre dans un tableau, ce n’est pas nécessairement simple

str(m)

List of 13
 $ coefficients : Named num [1:2] -4.942 0.742
  ..- attr(*, "names")= chr [1:2] "(Intercept)" "log(bodywt)"
 $ residuals    : Named num [1:20] -0.6656 0.6216 0.1733 -0.0253 0.5345 ...
  ..- attr(*, "names")= chr [1:20] "2" "4" "5" "6" ...
 $ effects      : Named num [1:20] 15.3808 12.0043 0.3263 -0.0469 0.4878 ...
  ..- attr(*, "names")= chr [1:20] "(Intercept)" "log(bodywt)" "" "" ...
 $ rank         : int 2
 $ fitted.values: Named num [1:20] -0.195 -2.942 -2.336 -5.178 -5.586 ...
  ..- attr(*, "names")= chr [1:20] "2" "4" "5" "6" ...
 $ assign       : int [1:2] 0 1
 $ qr           :List of 5
  ..$ qr   : num [1:20, 1:2] -4.472 0.224 0.224 0.224 0.224 ...
  .. ..- attr(*, "dimnames")=List of 2
  .. .. ..$ : chr [1:20] "2" "4" "5" "6" ...
  .. .. ..$ : chr [1:2] "(Intercept)" "log(bodywt)"
  .. ..- attr(*, "assign")= int [1:2] 0 1
  ..$ qraux: num [1:2] 1.22 1.01
  ..$ pivot: int [1:2] 1 2
  ..$ tol  : num 1e-07
  ..$ rank : int 2
  ..- attr(*, "class")= chr "qr"
 $ df.residual  : int 18
 $ na.action    : 'omit' Named int [1:12] 1 3 12 13 15 17 19 21 22 25 ...
  ..- attr(*, "names")= chr [1:12] "1" "3" "12" "13" ...
 $ xlevels      : Named list()
 $ call         : language lm(formula = log(brainwt) ~ log(bodywt), data = x)
 $ terms        :Classes 'terms', 'formula'  language log(brainwt) ~ log(bodywt)
  .. ..- attr(*, "variables")= language list(log(brainwt), log(bodywt))
  .. ..- attr(*, "factors")= int [1:2, 1] 0 1
  .. .. ..- attr(*, "dimnames")=List of 2
  .. .. .. ..$ : chr [1:2] "log(brainwt)" "log(bodywt)"
  .. .. .. ..$ : chr "log(bodywt)"
  .. ..- attr(*, "term.labels")= chr "log(bodywt)"
  .. ..- attr(*, "order")= int 1
  .. ..- attr(*, "intercept")= int 1
  .. ..- attr(*, "response")= int 1
  .. ..- attr(*, ".Environment")=<environment: R_GlobalEnv> 
  .. ..- attr(*, "predvars")= language list(log(brainwt), log(bodywt))
  .. ..- attr(*, "dataClasses")= Named chr [1:2] "numeric" "numeric"
  .. .. ..- attr(*, "names")= chr [1:2] "log(brainwt)" "log(bodywt)"
 $ model        :'data.frame':	20 obs. of  2 variables:
  ..$ log(brainwt): num [1:20] -0.86 -2.32 -2.16 -5.2 -5.05 ...
  ..$ log(bodywt) : num [1:20] 6.397 2.695 3.512 -0.317 -0.868 ...
  ..- attr(*, "terms")=Classes 'terms', 'formula'  language log(brainwt) ~ log(bodywt)
  .. .. ..- attr(*, "variables")= language list(log(brainwt), log(bodywt))
  .. .. ..- attr(*, "factors")= int [1:2, 1] 0 1
  .. .. .. ..- attr(*, "dimnames")=List of 2
  .. .. .. .. ..$ : chr [1:2] "log(brainwt)" "log(bodywt)"
  .. .. .. .. ..$ : chr "log(bodywt)"
  .. .. ..- attr(*, "term.labels")= chr "log(bodywt)"
  .. .. ..- attr(*, "order")= int 1
  .. .. ..- attr(*, "intercept")= int 1
  .. .. ..- attr(*, "response")= int 1
  .. .. ..- attr(*, ".Environment")=<environment: R_GlobalEnv> 
  .. .. ..- attr(*, "predvars")= language list(log(brainwt), log(bodywt))
  .. .. ..- attr(*, "dataClasses")= Named chr [1:2] "numeric" "numeric"
  .. .. .. ..- attr(*, "names")= chr [1:2] "log(brainwt)" "log(bodywt)"
  ..- attr(*, "na.action")= 'omit' Named int [1:12] 1 3 12 13 15 17 19 21 22 25 ...
  .. ..- attr(*, "names")= chr [1:12] "1" "3" "12" "13" ...
 - attr(*, "class")= chr "lm"

m$coefficients

(Intercept) log(bodywt) 
  -4.942134    0.742122

Dans le tidyverse il existe un package fait exprès pour extraire les résultats des modèles et les mettre sous forme de tableau

library(broom)
tidy(m)

# A tibble: 2 x 5
  term        estimate std.error statistic  p.value
  <chr>          <dbl>     <dbl>     <dbl>    <dbl>
1 (Intercept)   -4.94     0.125      -39.6 5.69e-19
2 log(bodywt)    0.742    0.0301      24.7 2.48e-15

On aurait pu aussi s’intéresser aux résultats du modèle plutôt qu’aux paramètres

glance(m)

# A tibble: 1 x 11
  r.squared adj.r.squared sigma statistic  p.value    df logLik   AIC   BIC
      <dbl>         <dbl> <dbl>     <dbl>    <dbl> <int>  <dbl> <dbl> <dbl>
1     0.971         0.970 0.486      609. 2.48e-15     2  -12.9  31.8  34.8
# … with 2 more variables: deviance <dbl>, df.residual <int>

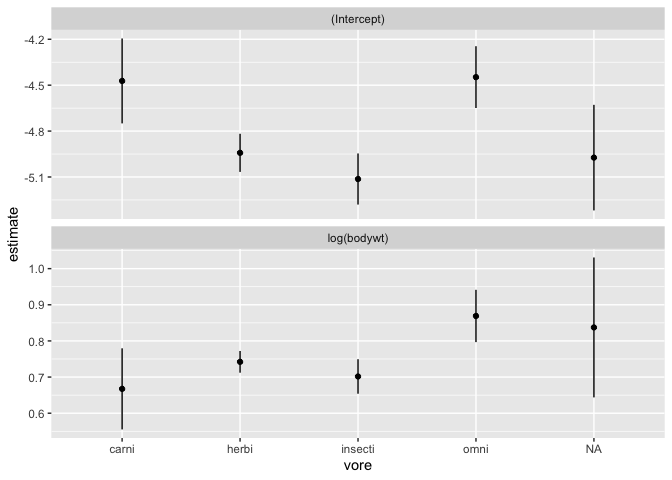
Maintenant, on a tout ce qu’il faut pour calculer une régression par groupe

resultats <- msleep %>% 
  group_by(vore) %>% 
  group_modify(function(x,...){
    m <- lm(log(brainwt)~log(bodywt),data = x)
    tidy(m)
  })
resultats

# A tibble: 10 x 6
# Groups:   vore [5]
   vore    term        estimate std.error statistic  p.value
   <chr>   <chr>          <dbl>     <dbl>     <dbl>    <dbl>
 1 carni   (Intercept)   -4.47     0.278     -16.1  8.61e- 7
 2 carni   log(bodywt)    0.667    0.112       5.95 5.71e- 4
 3 herbi   (Intercept)   -4.94     0.125     -39.6  5.69e-19
 4 herbi   log(bodywt)    0.742    0.0301     24.7  2.48e-15
 5 insecti (Intercept)   -5.11     0.167     -30.6  7.66e- 5
 6 insecti log(bodywt)    0.702    0.0477     14.7  6.84e- 4
 7 omni    (Intercept)   -4.45     0.202     -22.0  7.76e-13
 8 omni    log(bodywt)    0.869    0.0724     12.0  4.28e- 9
 9 <NA>    (Intercept)   -4.97     0.345     -14.4  7.23e- 4
10 <NA>    log(bodywt)    0.837    0.194       4.33 2.28e- 2

Voyez que comme pour les boucles, on s’est assuré de faire fonctionner notre code avant de l’intégrer au processus d’itération

On peut maintenant se faire une belle visualisation de tout cela en une seule commande

resultats %>% 
  ggplot(aes(x = vore, y = estimate)) +
  geom_point() +
  geom_linerange(aes(ymin = estimate-std.error, ymax = estimate+std.error)) +
  facet_wrap(~term, scale = "free_y", ncol = 1)