Méta-analyses

Charles Martin

Décembre 2019

library(dplyr) # data manipulation
library(ggplot2) # visualisations
library(metafor) # meta analyses déjà prêtes
library(gt) # beaux tableaux

Principe

Question de départ

Question de départ : Est-ce que jouer du Mozart aux nouveaux-nés augmente leur QI?

Vous trouvez 3 études :

etudes <- data.frame(
  article = c("A","B","C"),
  y = c(0.5, 0.01, -0.1), # 0 pas d'effet, <0 effet négatif, >0 effet positif
  n = c(10,150,12),
  v = c(0.04,0.01, 0.03) # variance
)
etudes %>% gt
article y n v
A 0.50 10 0.04
B 0.01 150 0.01
C -0.10 12 0.03

Façon bête

etudes %>%
  summarise(
    effet_resume = mean(y)
  )

  effet_resume
1    0.1366667

Moyenne pondérée

Moyenne arithmétique standard

(1 + 2 + 3 + 4) / 4

[1] 2.5

Implicitement, on donne un poids égal à chaque élément :

(1*1 + 1*2 + 1*3 + 1*4) / (1 + 1 + 1 + 1)

[1] 2.5

Mais on aurait pu donner un poids plus grand à certains éléments, p. ex. donner plus de poids aux plus récents

(0.125*1 + 0.25*2 + 0.5*3 + 1*4) / (0.125 + 0.25 + 0.5 + 1)

[1] 3.266667

Il existe une fonction de R qui nous permet de faire ce travail :

weighted.mean(
  c(1,2,3,4),
  c(0.125,0.25,0.5,1)
)

[1] 3.266667

La méta-analyse est une moyenne pondérée

Plus une étude est précise, plus son poids sera élevé dans le calcul de l’effet moyen

Une des façons classiques est d’utiliser comme poids l’inverse de la variance.

ATTENTION : il existe deux définitions de variance

La variance classique d’un échantillon est habituellement définie par : v = sum( (x-mean(x))^2 / (length(x)-1) )

Celle-ci nous permet de calculer l’écart-type d’un échantillon : sd = sqrt(v).

Ces deux mesures sont des statistiques descriptives.

On se rapelle que, pour passer de l’écart-type d’un échantillon à l’erreur type d’un paramètre (l’erreur autour de son estimé), on utilise la formule :

se = sd / sqrt(n)

Par contre, dans le livre de Borenstein, lorsque l’on parle de variance, on parle plutôt de la variance autour d’un estimé (la variance de l’erreur, sampling variance), qui correspond à l’erreur type au carré : v = se^2

Exemples de calculs

Et donc, on peut calculer notre première méta-analyse comme ceci :

etudes %>%
  summarise(
    effet_pondere = weighted.mean(y,1/v)
  )

  effet_pondere
1    0.06421053

Avec le package metafor, on a le même calcul :

m <- rma(
  yi = y,
  vi = v,
  data = etudes,
  method = "FE"
)
m


Fixed-Effects Model (k = 3)

Test for Heterogeneity:
Q(df = 2) = 5.9405, p-val = 0.0513

Model Results:

estimate      se    zval    pval    ci.lb   ci.ub   
  0.0642  0.0795  0.8080  0.4191  -0.0916  0.2200   

---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Mais en plus on obtient un intervalle de confiance autour de notre valeur moyenne (et d’autres choses que l’on verra plus tard).

Dans notre cas, l’intervalle de confiance à 95% de notre effet n’exlut pas zéro, donc pas d’effet significatif de jouer du Mozart aux nouveaux-nés

Sélection des études

Toujours mieux d’utiliser une méthode reproductible, p. ex. de définir une recherche dans Scopus (https://www2.scopus.com/search/form.uri?display=basic): TITLE-ABS-KEY ( music AND ( baby OR toddler OR newborn ) AND ( iq OR intelligence ) )

Puis exportez cette liste d’articles pour figer votre recherche.

Il est souvent recommandé d’inspecter la bibliographie de chacun des articles pour être certains que vous n’avez rien manqué.

Aussi, gardez une trace détaillée de toutes les étapes de construction et d’élimination. Vous aurez besoin de les citer dans le texte (ou sous forme la d’un diagramme PRISMA). P. ex.

Taille de l’effet

Problématique

Il est peu probable que l’ensemble de vos études aient mesuré l’effet recherché exactement de la même manière.

Dans notre exemple, on pourrait retrouver :

Une mesure comme la corrélation ne possède pas d’échelle, mais les autres sont dépendantes de la façon dont elles ont été mesurées et devront être standardisées pour être comparées

Standardisation de la taille des effets

Il existe des dizaines de façons de standardiser les mesures, selon que l’on parle de différences de moyennes, de pentes, de comparaisons de proportions, etc.

Dans tous les cas, l’idée est de trouver une mesure qui fait abstraction de l’échelle.

P. ex., pour les différences de moyennes, on utilise souvent le d de Cohen. Son calcul ressemble beaucoup au calcul de la statistique de t :

d = (x1 - x2) / S_within

Pour chacune de ces mesures de taille d’effet, il existe aussi une mesure de variance (sensu Borenstein et al. 2011).

V_d = (n1 + n2 / n1*n2) + (d^2 / 2*(n1+n2))

Parfois, certaines mesures doivent aussi être converties parce que leur distribution ne convient pas à des calculs de méta-analyse. P. ex., le r de la corrélation doit être convertit en z de Fisher, parce que la variance de r n’est pas homogène à travers le spectre des valeurs.

z = 0.5 * log((1+r)/(1-r))

V_z = 1/(n-3)

Automatisation

Il existe une fonction dans metafor qui permet de faciliter le calcul des effets standardisés. Par contre, il faut que toutes nos mesures soient d’un même type (p. ex. toutes des corrélations)

etudes2 <- data.frame(
  etude = c("A","B"),
  r = c(0.6, -0.2),
  n = c(32,16)
)
escalc(
  measure = "ZCOR",
  ri = r,
  ni = n,
  data = etudes2
) %>%
  gt
etude r n yi vi
A 0.6 32 0.6931472 0.03448276
B -0.2 16 -0.2027326 0.07692308

Uniformisation

Un des problèmes auquel on fait souvent face, est que nous avons plusieurs types de mesures (corrélations, différences de moyennes, etc.) et que la taille d’effet standardisée pour chacun peut être différente. On arrive souvent à un point où on a des d de Cohen, des z des Fisher, des g de Hedges etc.

Il existe tout un chapitre du livre de Borenstein consacré uniquement aux conversions entre les tailles d’effet, tous les calculs sont là!

Problématiques typiques à l’écologie

Si vous étudiez des pentes, vous devrez les convertir manuellement en corrélations avant leur inclusion. Ce n’est pas nécéssairement simple.

Si vous avez accès aux données brutes, sachant que la formule de la pente est : slope = r*(Sy / Sx) on peut convertir une pente en corrélation en la divisant par le ratio Sy/Sx

Par contre, si vous n’avez pas accès aux écarts-types, il est possible d’y arriver par un chemin plus tortueux incluant la valeur de t et les degrés de liberté. Les équations sont dans un article difficile à trouver de 1982. Vous passerez me voir rendu là…

Pour notre exemple

Les données utilisées pour notre étude de cas étaient déjà prêtes dans un effet standardisé, le log-response ratio.

Autrement dit, le log du ratio entre les réponses avec et sans musique.

Sans le log, nos chiffres auraient ressemblé à

etudes %>%
  mutate(R = exp(y)) %>%
  gt
article y n v R
A 0.50 10 0.04 1.6487213
B 0.01 150 0.01 1.0100502
C -0.10 12 0.03 0.9048374

Autrement dit, 64% d’augmentation, 1% d’augmentation et 10% de diminution du QI

Par contre, le problème lorsque l’on modélise de tels ratios est que la partie <1 est “coincée” entre 0 et 1, alors que la partie >1 peut exploser dans des valeurs très grandes. Les mesures ne sont pas symétriques à gauche et à droite de 1

1/100 # 0.99 sous 1

[1] 0.01

100/1 # 99 au dessus de 1

[1] 100

La transformation log permet de rétablir cette symétrie

log(1/100) # 4.6 sous zéro

[1] -4.60517

log(100/1) # 4.6 au-dessus de zéro

[1] 4.60517

Visualisation

La visualisation classique d’une méta-analyse est ce que l’on nomme le forest plot :

forest(m, order = "obs", slab = etudes$article)

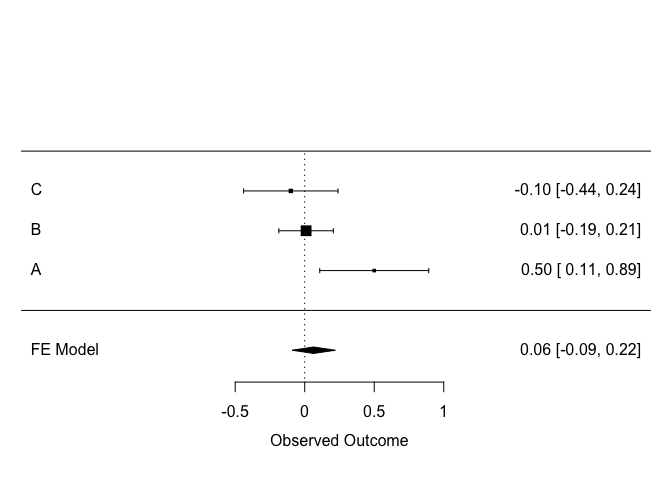
Chaque étude est représentée par une ligne. L’effet mesurée dans chaque étude est affiché, avec son intervalle de confiance. La taille du point correspond au poids de l’étude dans le calcul.

La dernière ligne correspond à l’effet global, tel que calculé plus haut.

Il peut parfois être utile de convertir la taille de l’effet à l’inverse (back-transform) pour retourner à une version plus facile à interpréter.

exp(-0.09)

[1] 0.9139312

exp(0.22)

[1] 1.246077

Donc, la vraie taille de l’effet est quelque part entre une augmentation de 25% et une diminution de 9% (95% des chances que…)

Le fameux biais de publication

Un des problèmes avec une méta-analyse basée sur la littérature est qu’il pourrait arriver que les études contraires aux résultats communément attendus n’aient pas été publiées, qu’ils soient restées dans les tiroirs.

Visualisation

Une des façons de visualiser ce problème est grâce au diagramme en entonnoir (funnel plot)

funnel(m)

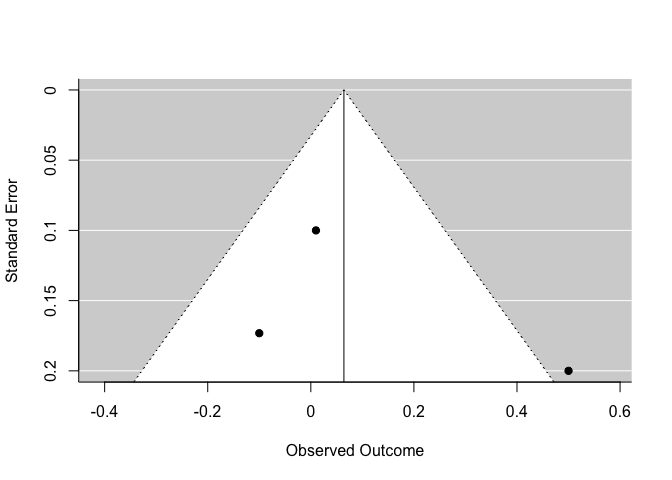
En y, on trouve la précision de chaque étude, et en x, l’estimé comme tel. Normalement, plus une étude est précise, plus elle devrait être près de la moyenne globale. Dans le bas de l’entonnoir, les études les moins précises devraient varier plus autour de la moyenne.

Il faut être particulièrement vigilant si ce diagramme n’est pas symétrique (e.g. si il y a beaucoup plus de points d’un côté que de l’autre).

Tests statistiques

Il existe aussi des tests statistiques pour valider nos impressions du funnel plot.

regtest(m, model = "lm", predictor = "sei")


Regression Test for Funnel Plot Asymmetry

model:     weighted regression with multiplicative dispersion
predictor: standard error

test for funnel plot asymmetry: t = 0.6405, df = 1, p = 0.6373

Le test de Egger classique est essentiellement une régression de l’estimé en fonction de l’erreur type (lm(y~sqrt(v), weights = 1/v, data = etudes))

etudes %>%
  ggplot(aes(x = sqrt(v), y = y)) +
  geom_point(aes(size = 1/v)) +
  geom_smooth(method = "lm") # attention, il faudrait aussi ajuster le poids de chaque observation à 1/v

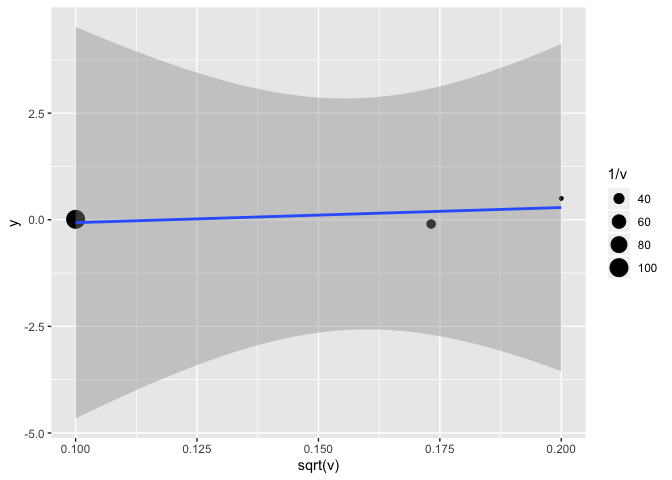
Il existe d’autres façons de tester pour le biais de publication, par exemple par des analyses de sensibilité.

Une de ces méthodes est le Trim & Fill. L’algorithme estime combien d’études sont manquantes d’un côté de l’analyse, puis recalcule notre estimé en ajoutant ces études fantômes. Ce nouvel estimé ne doit pas être interprété comme étant plus valide que l’original, il doit être uniquement utilisé pour évaluer la robustesse/sensibilité de nos résultats.

(exemple avec un autre jeu de données, puisqu’il n’y en a pas de manquantes de le nôtre)

res <- rma(yi, vi, data = dat.hackshaw1998)
taf <- trimfill(res)
funnel(taf)


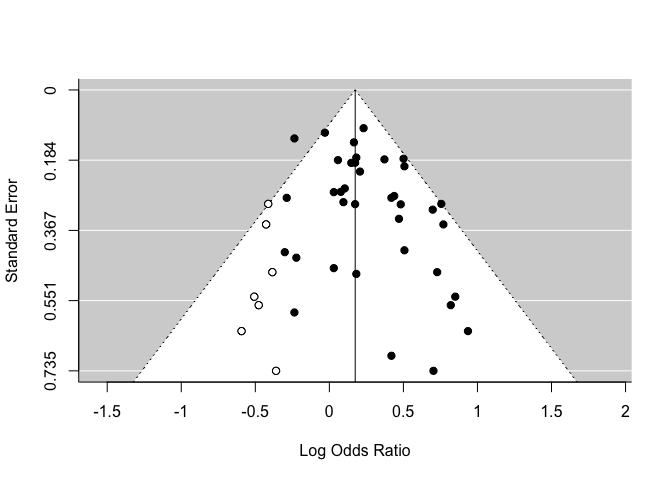
taf


Estimated number of missing studies on the left side: 7 (SE = 4.0399)

Random-Effects Model (k = 44; tau^2 estimator: REML)

tau^2 (estimated amount of total heterogeneity): 0.0245 (SE = 0.0183)
tau (square root of estimated tau^2 value):      0.1565
I^2 (total heterogeneity / total variability):   28.86%
H^2 (total variability / sampling variability):  1.41

Test for Heterogeneity:
Q(df = 43) = 60.5196, p-val = 0.0400

Model Results:

estimate      se    zval    pval   ci.lb   ci.ub     
  0.1745  0.0484  3.6015  0.0003  0.0795  0.2694  ***

---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Modèle à effets fixes vs. modèle à effets aléatoire

Jusqu’ici, nous avons exploré un modèle simple de méta-analyse, où nous assumions qu’en l’absence d’erreur (de bruit, etc.), toutes les études auraient dû nous donner le même résultat.

Il est possible par contre (et c’est presque toujours le cas en écologie), que la taille de l’effet dépende en fait du contexte dans lequel l’étude a été effectuée ou du groupe d’individus étudiés.

Dans notre exemple de l’effet de Mozart, on pourrait envisager un scénario où l’effet de la musique soit p. ex. différent selon le contexte culturel.

À ce moment, nous ne cherchons plus un seul effet synthétique absolu, identique à toutes les études. Nous assumons qu’il existe une population d’effets possibles qui dépendent du contexte. L’erreur dans l’effet mesuré provient alors de deux sources : l’erreur interne à chaque étude, et la variabilité entre les études (tau). On doit alors appliquer un modèle avec effets aléatoires.

Implications

Le modèle à effets aléatoires ajoute une composante de variance supplémentaire qui doit être estimée dans le modèle (tau^2). Le calcul est donc plus complexe et doit passer par la vraisemblance maximale (et les possibles erreurs de convergence etc.) alors que le modèle fixe peut être résolu par la méthode des moindres carrés.

Plus important conceptuellement, le poids donné à chaque étude sera différent dans le modèle à effets aléatoires. Puisque notre modèle doit être représentatif de la variabilité inter-études, il doit être plus équilibré dans son attribution des poids. Même si une étude est peu précise, l’information qu’elle apporte quand à la variabilité inter-études doit tout de même être prise en compte (et vice-versa, une étude très précise devra avoir un poids moins grand pour ne pas faire complètement disparaître l’effet des autres)

Calcul

Dans le package metafor, les modèles à effets aléatoires sont ajustés avec la même fonction que le modèle à effets fixes, mais en ne spécifiant pas la méthode FE

m2 <- rma(
  yi = y,
  vi = v,
  data = etudes
)
m2


Random-Effects Model (k = 3; tau^2 estimator: REML)

tau^2 (estimated amount of total heterogeneity): 0.0574 (SE = 0.0827)
tau (square root of estimated tau^2 value):      0.2397
I^2 (total heterogeneity / total variability):   70.75%
H^2 (total variability / sampling variability):  3.42

Test for Heterogeneity:
Q(df = 2) = 5.9405, p-val = 0.0513

Model Results:

estimate      se    zval    pval    ci.lb   ci.ub   
  0.1132  0.1655  0.6843  0.4938  -0.2111  0.4375   

---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Le résultat est semblable au précédent, mais il est plus conservateur, moins influencé par la grande étude très précise.

Notre tableau des résultats contient maintenant des informations supplémentaires. Tau^2 est la variance inter-études (qui a peu d’importance en absolu). I^2 par contre est beaucoup plus intéressant, puisqu’il s’agit de la proportion de la variabilité totale du jeu de données qui provient de l’hétérogénéité inter-études. Plus ce chiffre est élevé, plus les études sont différentes entre elles.

Nos résultats (comme les précédents) fournissent le résultat d’un test d’hétérogénéité, qui nous informe si l’hétérogénéité est significative ou non. On pourrait être tenté de se baser sur ce test pour savoir si on doit utiliser un modèle à effets aléatoires ou non, mais comme pour les effets aléatoires dans un modèle de régression, si conceptuellement on devrait mettre l’effet aléatoire, il est fortement recommandé de simplement l’ajouter au modèle.

Références

Borenstein, M., Hedges, L. V., Higgins, J. P., & Rothstein, H. R. (2011). Introduction to meta-analysis. John Wiley & Sons.

Viechtbauer, W. (2010). Conducting meta-analyses in R with the metafor package. Journal of Statistical Software, 36(3), 1-48. URL: http://www.jstatsoft.org/v36/i03/

Viechtbauer, W. (2021). The metafor Package: A Meta-Analysis Package for R. https://www.metafor-project.org/doku.php/metafor