Les modèles non-linéaires

Charles Martin

Février 2024

Introduction

Une des contraintes classique des modèles linéaires est que, par définition, ils décrivent des relations linéaires entre les variables. Hors, dans la vraie vie, il arrivera souvent que ce que nous voulons modéliser suive une série d’autres formes.

Il existe par ailleurs une panoplie façons dont nos relations seraient non-linéaires. On peut observer entre autres des fonctions en escalier, des relations présentant différentes pentes à travers un gradient et évidemment, des fonctions en courbe à proprement parler.

Incidemment, cet atelier portera sur une série de techniques différentes, pouvant être appliquées à ces différentes situations.

Comme d’habitude, cet atelier assume une maîtrise de base de la manipulation des données et de la visualisation dans R, mais chaque étape sera néanmoins expliquée, même celles de préparation.

Aussi, comme les autres ateliers du Numérilab, cet atelier n’est qu’un survol des différentes techniques, et ne remplace pas une lecture attentive des références décrivant chacune des techniques plus en détail.

Librairies nécessaires

Nous aurons besoin pour travailler aujourd’hui de 5 librairies principales, soit :

library(tidyverse) # Pour manipuler et visualiser nos données

Warning: package 'ggplot2' was built under R version 4.3.1

library(changepoint) # Pour détecter des changements de moyenne ou variance
library(cpop) # Pour détecter des changements de pente
library(mgcv) # Pour modéliser des courbes arbitraires avec des fonctions de lissage
library(ggthemes) # Pour la palette de couleur pour les daltoniens

Changements dans un paramètre

Préparation des données

Dans R, il existe une série de données mensuelles relativement récentes sur l’économie américaine, sans besoin de rien charger. Par exemple, on peut rapidement effectuer ce graphique sur la durée médiane des périodes de chômage :

economics %>% 
  ggplot(aes(date, uempmed)) +
  geom_line()

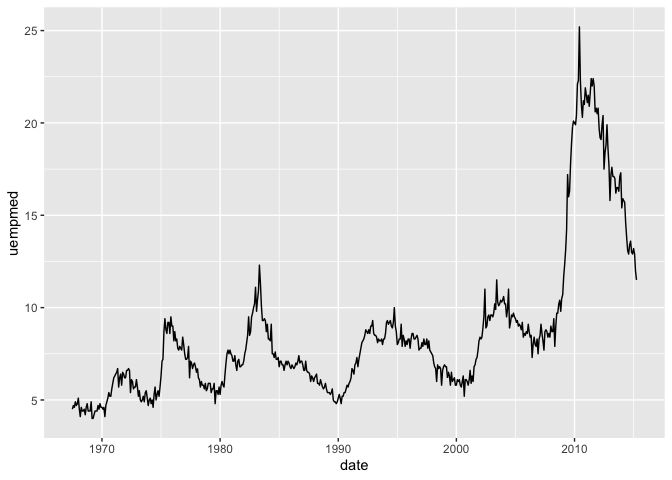
Pour notre première exploration des changements dans la valeur d’un paramètre, nous regardons l’effet de chaque président sur le chômage.

Pour simplifier nos analyses, nous allons garder que les données depuis 1989, et ajouter une variable qualitative représentant le président en fonction à cette époque

donnees_chomage <- economics %>% 
  filter(date >= "1989-01-20") %>% 
   mutate(
     chomage_pct = unemploy / pop * 100,
     president = case_when(
      .default = "Bush père",
      date > "2009-01-20" ~ "Obama",
      date > "2001-01-20" ~ "Bush fils",
      date > "1993-01-20" ~ "Clinton"
  ))

Voici donc à quoi ressemble nos données :

fond_graphique <- donnees_chomage %>% 
  ggplot(aes(date,chomage_pct)) +
  geom_ribbon(aes(ymin = 0, ymax = 6,fill = president), alpha = 0.4) +
  geom_line() +
  theme_minimal() +
  scale_fill_colorblind() +
  labs(x = "Date", y = "Chômage (%)", fill = "Président")

fond_graphique

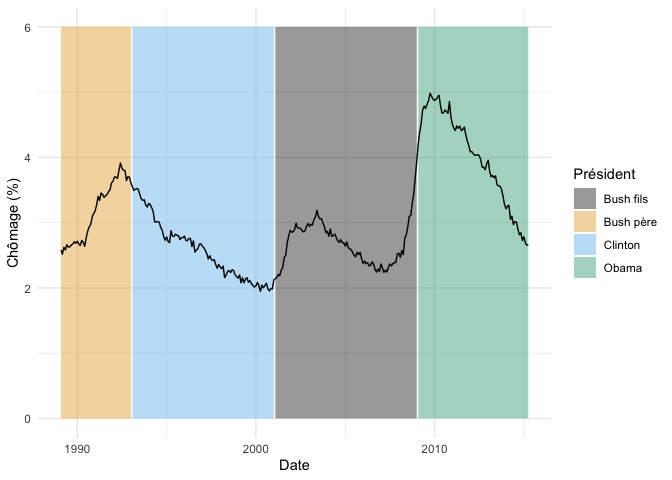
NB nous conservons ce graphique dans un objet, puisqu’il nous servira souvent de base dans les sections suivantes.

Fonctions en escalier (step function)

La façon la plus simple pour modéliser ce genre de question, est d’utiliser une variable qualitative plutôt que la date pour faire la modélisation. On modélise ainsi une sorte d’escalier (… step function) avec un changement à chacun des points prédéterminés.

m <- lm(chomage_pct ~ president, data = donnees_chomage)
summary(m)


Call:
lm(formula = chomage_pct ~ president, data = donnees_chomage)

Residuals:
     Min       1Q   Median       3Q      Max 
-1.34775 -0.38290  0.01925  0.32571  1.26021 

Coefficients:
                   Estimate Std. Error t value Pr(>|t|)    
(Intercept)         2.67764    0.05093  52.576  < 2e-16 ***
presidentBush père  0.49432    0.08821   5.604 4.62e-08 ***
presidentClinton   -0.09840    0.07202  -1.366    0.173    
presidentObama      1.32570    0.07690  17.239  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.499 on 311 degrees of freedom
Multiple R-squared:  0.5718,	Adjusted R-squared:  0.5677 
F-statistic: 138.5 on 3 and 311 DF,  p-value: < 2.2e-16

Comme c’est toujours le cas par défaut avec R, la première valeur de notre variable qualitative en ordre alphabétique (Bush fils) a été retenue comme valeur de référence à laquelle les autres sont comparées. On voit entre autres dans ces résultats qu’en moyenne, le taux de chômage pendant la période Omaba était 1.3 points de pourcentage au-dessus de celui de Bush fils.

À première vue, ce modèle est excellent puisque globalement significatif (< 2.2e-16) et explique à lui seul 57% de la variance dans le taux de chômage.

On peut visualiser le résultat de ce modèle en prédisant une valeur pour chacune des lignes de notre tableau :

fond_graphique +
  geom_line(
    data = donnees_chomage %>% mutate(prediction = predict(m)),
    aes(y = prediction),
    linetype = "dashed",
    color = "blue"
  )

Détection d’un point de changement (changepoint analysis)

Tout ça est bien beau si l’on connaît les dates de changements et que l’on veut évaluer leur impact sur la moyenne, mais qu’en est-il si on ne connaît pas d’avance les points de changements (ou si on veut les établir de façon objective)?

Entre en scène la librairie changepoint (Killick et Eckley 2014) ! Une des difficultés avec ce genre de question est qu’il existe une panoplie d’algorithmes différents pour répondre à cette question. L’avantage de la librairie changepoint est qu’elle implémente une variété d’algorithmes différents, permettant d’explorer facilement les alternatives.

Pourtant, à la base, le problème est plutôt simple. Si on prend le cas hypothétique où on cherche un seul changement, l’idée serait de faire une série de modèles comme celui ci-haut, pour chacun des points de changement possibles, et de conserver celui avec le meilleur ajustement. Dans le cas présent, on parlerait de 315 modèles différents à essayer. C’est gros, mais rien qu’un ordinateur moderne ne peut pas gérer en quelques secondes.

Par contre, si on ne sait pas combien de points de changement comptera notre série, la technique par force brute qui teste toutes les solutions devrait tester $2^{n-1}$ modèles, soit dans notre cas 1.66874e+94 modèles, ce qui est clairement irréalisable.

C’est pourquoi il existe au moins 3 algorithmes différents :

La fonction pour chercher des changements de moyenne avec la librairie changepoint se nomme cpt.mean.

Pour chercher dans notre jeu de données sur les présidents avec l’algorithme PELT, on ferait comme ceci :

changements <- cpt.mean(donnees_chomage$chomage_pct, method = "PELT")
summary(changements)

Created Using changepoint version 2.2.4 
Changepoint type      : Change in mean 
Method of analysis    : PELT 
Test Statistic  : Normal 
Type of penalty       : MBIC with value, 17.25772 
Minimum Segment Length : 1 
Maximum no. of cpts   : Inf 
Changepoint Locations : 238 288

La fonction nous informe qu’elle trouve deux points de changement, aux lignes 238 et 288 de notre série de données.

On peut visualiser ce ceux points de rupture sur un graphique, par exemple comme ceci :

fond_graphique + 
  geom_vline(
    data = donnees_chomage %>% slice(238,288), 
    aes(xintercept = date),
    linetype = "dashed"
  )

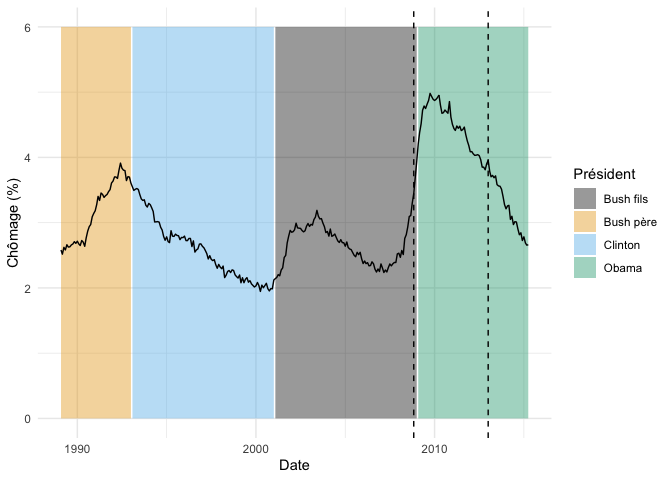
Donc, l’algorithme PELT détecte un point de changement au début du mandat de Obama, et un environ au milieu.

Ce qu’il est important de comprendre est que le fait de savoir si un point de coupure sera conservé ou non est basé sur un ratio de vraisemblance, accompagné d’une pénalité pour le nombre de point de coupure. La structure est donc semblable à celle utilisée pour calculer l’AIC, que l’ont peut d’ailleurs utiliser directement comme critère dans l’algorithme :

changements <- cpt.mean(
  donnees_chomage$chomage_pct, 
  method = "PELT",
  penalty = "AIC"
)
summary(changements)

Created Using changepoint version 2.2.4 
Changepoint type      : Change in mean 
Method of analysis    : PELT 
Test Statistic  : Normal 
Type of penalty       : AIC with value, 4 
Minimum Segment Length : 1 
Maximum no. of cpts   : Inf 
Changepoint Locations : 22 63 101 150 238 274 297

Cette version, beaucoup plus optimiste, détecte 7 points de changement :

fond_graphique + 
  geom_vline(
    data = donnees_chomage %>% slice(22, 63, 101, 150, 238, 274, 297), 
    aes(xintercept = date),
    linetype = "dashed"
  )

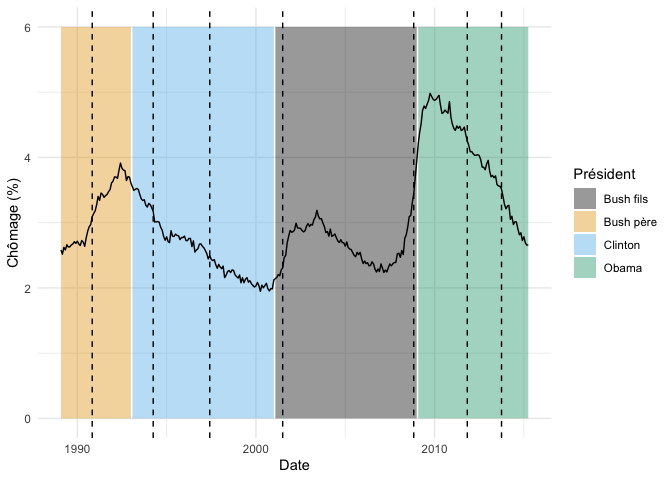
Comme pour les méthodes de regroupement (i.e. K-means, partitionnement hiérarchique), il n’existe pas de façon absolue de déterminer le nombre de points de ruptures dans une série de données. La pénalité pour le nombre de coupures sera toujours arbitraire et votre jugement aura inévitablement un rôle à jouer.

Enfin, il existe aussi dans la librairie une fonction pour chercher les changements de variance (cpt.var) et une autre pour chercher les changements de moyenne ET de variance (cpt.meanvar).

Changements de pente

Dans la section précédente, nous nous sommes intéressés aux changements dans la moyenne entre différentes sections d’une série de données. Maintenant, nous nous demanderons si la pente, elle, change à différents points dans la série.

Si on repense à notre jeu de données sur le taux de chômage, notre question dans la section précédente était “Est-ce que la moyenne de chômage varie entre les présidents”. Ici, nous nous demanderons si les variations dans le taux de chômage changent selon les présidents. C’est-à-dire, est-ce que pour certains le chômage augmente, ou diminue, indépendamment de la moyenne au début du mandat.

Méthode intuitive

Une façon plutôt intuitive de répondre à cette question serait de prendre chaque valeur de la série, et de lui soustraire la valeur précédente. On calcule la première différence. Cette série de premières différences sera positive si le chômage augmente pendant une période et négative si le chômage diminue. On pourra ensuite appliquer les méthodes de la section précédente sur ces premières différences pour détecter des points de changement.

donnees_chomage <- donnees_chomage %>% 
  mutate(
    premiere_difference = chomage_pct - lag(chomage_pct)
  ) %>% 
  drop_na(premiere_difference)

donnees_chomage %>% 
  ggplot(aes(date, premiere_difference)) +
  geom_line()


cpt.mean(
  donnees_chomage$premiere_difference, 
  method = "PELT"
) %>% 
  summary()

Created Using changepoint version 2.2.4 
Changepoint type      : Change in mean 
Method of analysis    : PELT 
Test Statistic  : Normal 
Type of penalty       : MBIC with value, 17.24818 
Minimum Segment Length : 1 
Maximum no. of cpts   : Inf 
Changepoint Locations :

Comme vous le constatez, malheureusement, cette façon intuitive ne fonctionne pas très bien. Ici, l’algorithme ne détecte aucun changement, bien que visuellement, la tendance de certains présidents est très claire, p. ex. la diminution pendant les mandats d’Obama. Ce phénomène est confirmé par les auteurs de la librairie cpop.

cpop

Nous avons donc besoin d’une façon de construire la meilleure fonction linéaire par morceaux (piecewise-linear function). La solution proposée par Farnhead & Grose de la librairie cpop est, un peu comme pour les méthodes précédentes, d’ajuster un modèle avec de multiples pentes et d’en minimiser la somme des carrés, tout en tenant compte d’une pénalité pour le nombre de pentes différentes ajustées. Aussi, comme pour l’algorithme PELT, la solution de cpop consiste à utiliser la programmation dynamique récursive pour ajuster ce modèle.

Les auteurs de librairie parlent d’une pénalité de type $L_0$, c’est à dire que chaque changement de pente coûte la même chose en terme de pénalité, contrairement aux pénalités de type $L_1$, utilisées entre autres pour filtrer des signaux, qui elles pénalisent proportionnellement à l’ampleur du changement de pente.

Donc, si on veut essayer l’algorithme CPOP avec toutes ses valeurs par défaut, on peut le faire ainsi :

resultats <- cpop(
  donnees_chomage$chomage_pct, 
  as.numeric(donnees_chomage$date)
)

No value set for beta, so the default value of beta=2log(n), where n is the number of data points, has been used. This default value is appropriate if the noise is IID Gaussian and the value of sd is a good estimate of the standard deviation of the noise. If these assumptions do not hold, the estimate of the number of changepoints may be inaccurate. To check robustness use cpop.crops with beta_min and beta_max arguments.

No value set for sd. An estimate for the noise standard deviation based on the variance of the second differences of the data has been used. If this estimate is too small it may lead to over-estimation of changepoints. You are advised to check this by comparing the standard deviation of the residuals to the estimated value used for sd.

Length of sd and y differ. Applying first value of sd to all values of y.

Plusieurs choses sont à noter ici.

Tout d’abord, remarquez que l’on doit convertir nos dates en chiffres (nombre de jours depuis 1970-01-01) pour utiliser la fonction qui ne supporte pas le format Date. Ensuite, la fonction nous fournit deux avertissements.

Premièrement, elle nous informe que nous avons pas choisit de pénalité ($\beta$). La fonction a donc choisi pour nous $\beta = 2log(n)$, qui est approprié si nos données sont distribuées normalement.

Deuxièmement, la fonction nous informe qu’elle a calculé une estimation de l’écart-type de nos données, et que l’on devrait toujours vérifier si cette estimation correspond bien à nos données car des écarts pourraient fausser les résultats.

Ici, l’écart-type des résidus et celui estimé par cpop est TRÈS semblable, donc pas de raison de s’inquiéter de ces avertissements.

sd(residuals(resultats))

[1] 0.04139569

resultats@sd %>% unique()

[1] 0.04069121

Observons maintenant les résultats :

summary(resultats)


cpop analysis with n = 314 and penalty (beta)  = 11.49879

26  changepoints detected at x = 
 7456 7729 7913 8187 8825 9190 9221 9893 10166 11231 11504 11657 12112 12204 12387 13573 13970 14153 14365 14700 14761 14914 14975 15218 15340 15706
fitted values : 
      x0       y0    x1       y1      gradient   intercept          RSS
1   6999 2.598212  7456 2.707540  0.0002392289   0.9238490 0.0177944219
2   7456 2.707540  7729 3.364743  0.0024073371 -15.2415660 0.0085669471
3   7729 3.364743  7913 3.437702  0.0003965160   0.3000702 0.0087956454
4   7913 3.437702  8187 3.848474  0.0014991694  -8.4252260 0.0095473606
5   8187 3.848474  8825 3.179686 -0.0010482567  12.4305516 0.0367859336
6   8825 3.179686  9190 2.664178 -0.0014123506  15.6436807 0.0212652599
7   9190 2.664178  9221 2.844367  0.0058125308 -50.7529795 0.0009020615
8   9221 2.844367  9893 2.597673 -0.0003671046   6.2294386 0.0449915462
9   9893 2.597673 10166 2.321144 -0.0010129260  12.6185492 0.0074868018
10 10166 2.321144 11231 1.961889 -0.0003373284   5.7504244 0.0677525623
11 11231 1.961889 11504 2.312383  0.0012838599 -12.4571419 0.0077954158
12 11504 2.312383 11657 2.880832  0.0037153577 -40.4290928 0.0053334509
13 11657 2.880832 12112 2.955723  0.0001645947   0.9621520 0.0224953314
14 12112 2.955723 12204 3.175270  0.0023863783 -25.9480913 0.0006327371
15 12204 3.175270 12387 2.875918 -0.0016358030  23.1386095 0.0032815319
16 12387 2.875918 13573 2.218515 -0.0005543030   9.7420695 0.0708147051
17 13573 2.218515 13970 2.577250  0.0009036171 -10.0462802 0.0150043128
18 13970 2.577250 14153 3.278435  0.0038316089 -50.9503265 0.0141548009
19 14153 3.278435 14365 4.773794  0.0070535803 -96.5508871 0.0109426354
20 14365 4.773794 14700 4.958654  0.0005518202  -3.1531027 0.0290597025
21 14700 4.958654 14761 4.657511 -0.0049367726  77.5292103 0.0001209663
22 14761 4.657511 14914 4.779201  0.0007953626  -7.0828367 0.0077525907
23 14914 4.779201 14975 4.466564 -0.0051252027  81.2164745 0.0058983267
24 14975 4.466564 15218 4.434632 -0.0001314075   6.4343904 0.0069431556
25 15218 4.434632 15340 4.095616 -0.0027788152  46.7226413 0.0010642687
26 15340 4.095616 15706 3.858032 -0.0006491360  14.0533620 0.0254032772
27 15706 3.858032 16526 2.592724 -0.0015430586  28.0933106 0.0857720373

overall RSS = 0.5363578
cost = 622.9001

Les valeurs par défaut ont trouvé 27 (!) changements de pente.

Nous allons d’abord voir comment les visualiser, puis nous regarderons ensuite comment raffiner ce total.

fond_graphique +
  geom_vline(xintercept = as_date(resultats@changepoints[-1]), linetype = "dashed") +
  geom_segment(
    data = fitted(resultats), 
    aes(x=as_date(x0),y=y0,xend=as_date(x1),yend=y1),
    linewidth = 1,
    color = "blue"
  )

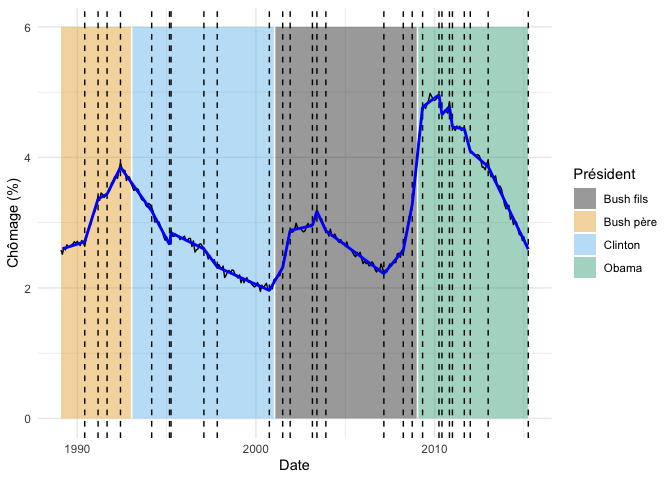
Le fait d’avoir beacoup de points de rupture de pente n’est pas nécessairement étonnant. Comme pour l’algorithme PELT, la pénalité utilisée dans l’algorithme CPOP est arbitraire et mérite d’être ajustée manuellement.

Si on impose une pénalité beaucoup plus forte, on obtient beaucoup moins de segments :

resultats2 <- cpop(
  donnees_chomage$chomage_pct, 
  as.numeric(donnees_chomage$date),
  beta = 40 * log(length(donnees_chomage$date))
)

No value set for sd. An estimate for the noise standard deviation based on the variance of the second differences of the data has been used. If this estimate is too small it may lead to over-estimation of changepoints. You are advised to check this by comparing the standard deviation of the residuals to the estimated value used for sd.

Length of sd and y differ. Applying first value of sd to all values of y.

fond_graphique +
  geom_vline(xintercept = as_date(resultats2@changepoints[-1]), linetype = "dashed") +
  geom_segment(
    data = fitted(resultats2), 
    aes(x=as_date(x0),y=y0,xend=as_date(x1),yend=y1),
    linewidth = 1,
    color = "blue"
  )

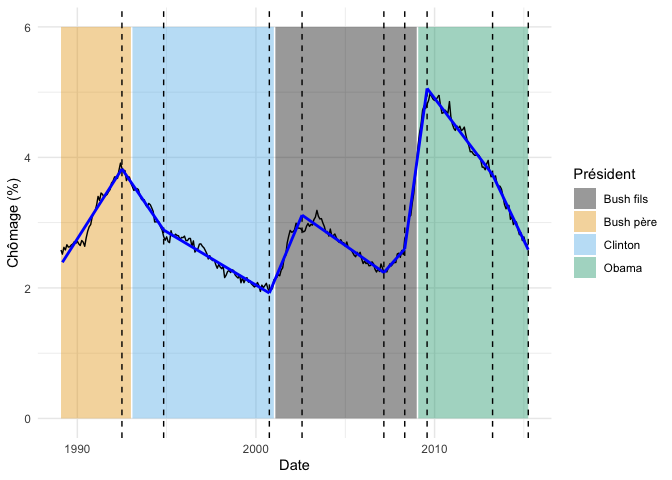
Il est d’ailleurs recommandé par les auteurs d’explorer différentes valeurs de $\beta$ avec la fonction cpop.crops.

Régression polynomiale

Si les relations que l’on étudie présentent des non-linéarités, il peut parfois être intéressant de pouvoir décrire mathématiquement la forme des courbes suivies par nos données.

Ici notre objectif n’est plus de savoir où sont les points de changement, mais bien de simplement décrire au mieux la courbe de nos données.

Pour se faire, l’outil classique est d’utiliser la régression polynomiale. C’est-à-dire de bonifier le modèle de régression standard \(y_i = \beta_0 + \beta_1x_i+\epsilon_i\)

avec des termes de degrés plus élevés, par exemple avec le carré et le cube de $x$ \(y_1 = \beta_0 + \beta_1x_i + \beta_2x_i^2 + \beta_3x_i^3 + \epsilon_i\)

L’implémentation des termes polynomiaux dans R est plutôt maladroite, car le symbole ^ a une signification spéciale qui ne correspond pas à un exposant. Une solution est d’emballer chaque terme polynomial par la fonction I, qui signifie à R de traiter notre ^ comme un exposant, par exemple I(x^2).

Il existe cependant une façon plus simple de noter la même chose, avec la fonction poly. Par exemple, si on veut une régression polynomiale avec $x$, $x^2$ et $x^3$, on peut inscrire simplement le terme poly(x,3).

Voyons comment cela peut s’appliquer avec nos données de chômage. Si on voulait ajuster une polynomiale de degré 3 sur les données, on pourrait faire comme ceci :

m_p <- lm(chomage_pct ~ poly(date,3), data = donnees_chomage)
summary(m_p)


Call:
lm(formula = chomage_pct ~ poly(date, 3), data = donnees_chomage)

Residuals:
     Min       1Q   Median       3Q      Max 
-1.16178 -0.48885 -0.00662  0.34664  1.54505 

Coefficients:
               Estimate Std. Error t value Pr(>|t|)    
(Intercept)      3.0401     0.0355  85.631  < 2e-16 ***
poly(date, 3)1   4.5287     0.6291   7.199 4.62e-12 ***
poly(date, 3)2   5.6006     0.6291   8.903  < 2e-16 ***
poly(date, 3)3  -2.4677     0.6291  -3.923 0.000108 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.6291 on 310 degrees of freedom
Multiple R-squared:  0.3209,	Adjusted R-squared:  0.3143 
F-statistic: 48.82 on 3 and 310 DF,  p-value: < 2.2e-16

On constate dans ces sorties que chacun des termes de notre polynomiale est significatif.

On peut visualiser ces résultats comme ceci, en extrayant d’abord les prédictions du modèle :

fond_graphique +
  geom_line(
    data = donnees_chomage %>% mutate(prediction = predict(m_p)),
    aes(y = prediction),
    linetype = "dashed",
    color = "blue"
  )

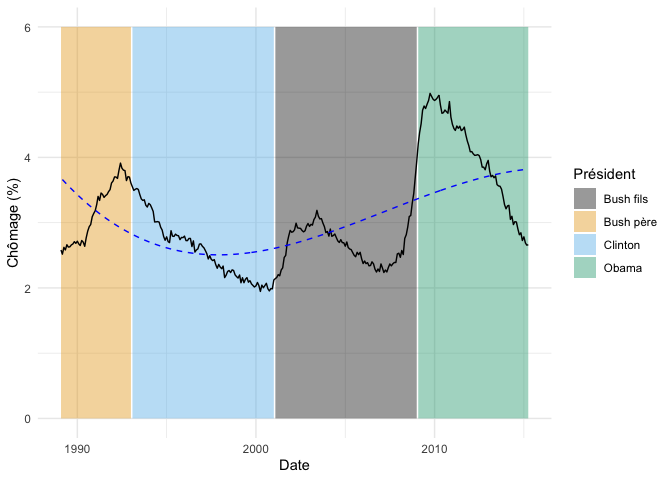
Clairement, notre modèle n’a pas assez de degrés de liberté pour s’ajuster à la courbe en entier.

On pourrait, par exemple, explorer l’effet de mettre des termes polynomiaux jusqu’au degré 8 :

m_p8 <- lm(chomage_pct ~ poly(date,8), data = donnees_chomage)
summary(m_p8)


Call:
lm(formula = chomage_pct ~ poly(date, 8), data = donnees_chomage)

Residuals:
     Min       1Q   Median       3Q      Max 
-0.70916 -0.20297  0.02085  0.21214  0.89890 

Coefficients:
               Estimate Std. Error t value Pr(>|t|)    
(Intercept)     3.04007    0.01783 170.534  < 2e-16 ***
poly(date, 8)1  4.52866    0.31589  14.336  < 2e-16 ***
poly(date, 8)2  5.60064    0.31589  17.730  < 2e-16 ***
poly(date, 8)3 -2.46771    0.31589  -7.812 9.16e-14 ***
poly(date, 8)4 -7.84761    0.31589 -24.843  < 2e-16 ***
poly(date, 8)5 -0.94162    0.31589  -2.981  0.00311 ** 
poly(date, 8)6 -2.58720    0.31589  -8.190 7.23e-15 ***
poly(date, 8)7  0.95184    0.31589   3.013  0.00280 ** 
poly(date, 8)8  4.70970    0.31589  14.909  < 2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.3159 on 305 degrees of freedom
Multiple R-squared:  0.8315,	Adjusted R-squared:  0.8271 
F-statistic: 188.2 on 8 and 305 DF,  p-value: < 2.2e-16

fond_graphique +
  geom_line(
    data = donnees_chomage %>% mutate(prediction = predict(m_p8)),
    aes(y = prediction),
    linetype = "dashed",
    color = "blue"
  )

On se rapproche ainsi beaucoup plus près de notre courbe originale.

On pourrait par la suite, soit avec une ANOVA ou l’AIC, comparer l’ajustement de différents modèles afin de sélectionner le nombre de termes polynomiaux le plus parcimonieux.

Une chose sur laquelle nous avons glissé jusqu’ici est que l’ajout de termes polynomiaux (i.e. $x^2, x^3…x^n$) à un modèle linéaire augmente beaucoup l’instabilité dans l’estimation de ses paramètres puisque ces termes sont inévitablement très corrélés les uns aux autres.

C’est pourquoi la fonction poly, par défaut, applique une transformation aux termes pour les rendre orthogonaux. On peut utiliser les termes polynomiaux bruts en ajoutant l’argument raw = TRUE à la fonction.

m_p_r <- lm(chomage_pct ~ poly(date,3, raw = TRUE), data = donnees_chomage)
summary(m_p_r)


Call:
lm(formula = chomage_pct ~ poly(date, 3, raw = TRUE), data = donnees_chomage)

Residuals:
     Min       1Q   Median       3Q      Max 
-1.16178 -0.48885 -0.00662  0.34664  1.54505 

Coefficients:
                             Estimate Std. Error t value Pr(>|t|)    
(Intercept)                 2.040e+01  3.232e+00   6.311 9.57e-10 ***
poly(date, 3, raw = TRUE)1 -4.388e-03  8.726e-04  -5.029 8.37e-07 ***
poly(date, 3, raw = TRUE)2  3.443e-07  7.612e-08   4.523 8.68e-06 ***
poly(date, 3, raw = TRUE)3 -8.441e-12  2.152e-12  -3.923 0.000108 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.6291 on 310 degrees of freedom
Multiple R-squared:  0.3209,	Adjusted R-squared:  0.3143 
F-statistic: 48.82 on 3 and 310 DF,  p-value: < 2.2e-16

Si l’on compare au modèle avec les termes orthogonaux…

summary(m_p)


Call:
lm(formula = chomage_pct ~ poly(date, 3), data = donnees_chomage)

Residuals:
     Min       1Q   Median       3Q      Max 
-1.16178 -0.48885 -0.00662  0.34664  1.54505 

Coefficients:
               Estimate Std. Error t value Pr(>|t|)    
(Intercept)      3.0401     0.0355  85.631  < 2e-16 ***
poly(date, 3)1   4.5287     0.6291   7.199 4.62e-12 ***
poly(date, 3)2   5.6006     0.6291   8.903  < 2e-16 ***
poly(date, 3)3  -2.4677     0.6291  -3.923 0.000108 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 0.6291 on 310 degrees of freedom
Multiple R-squared:  0.3209,	Adjusted R-squared:  0.3143 
F-statistic: 48.82 on 3 and 310 DF,  p-value: < 2.2e-16

Les paramètres du modèle et leurs intervalles de confiance seront différents, mais le $R^2$, la valeur de $p$ globale et les prédictions du modèle seront absolument identiques. Mais la version avec raw = TRUE, les estimations de paramètres seront moins stables.

GAM

Dernière technique que nous verrons aujourd’hui : les modèles additifs généralisés (GAM). Ces modèles sont une extension des modèles linéaires dans lesquels on peut inclure, au besoin, des termes de lissage permettant de définir des relations non-linéaires entre nos variables, mais qui ne sont pas contraintes par des termes polynomiaux comme ci-haut. L’inconvénient de cette liberté sera par contre que la relation ne pourra plus être définie par une équation avec des paramètres dans une formule. On obtiendra simplement une courbe, qu’il faudra interpréter plus qualitativement, mais qui pourra s’ajuster à n’importe quelle forme.

Pour lisser une courbe dans un modèle linéaire, il existe deux techniques majeures, avec des noms parfois difficile à démêler soit les splines de régression cubiques (cubic regression splines) et les splines de régression à plaques minces (thin plate regression splines).

PS Apparamment, dans ce contexte, il est correct d’utiliser le terme spline en français (voir https://fr.wikipedia.org/wiki/Spline)

Splines de régression cubiques

Les splines de régression cubiques sont probablement la technique la plus intuitive à comprendre des deux. L’idée est de séparer le gradient en X par une série de noeuds, que l’on connecte ensuite par une série de régressions polynomiales de degré 3 (le cubique). Afin que les segments forment une courbe lisse, une contrainte est ajoutée au moment d’ajuster le modèle, soit que les segments se connectent à une valeur commune, mais aussi que la première et la deuxième dérivée soient identiques. Autrement dit, que la pente, et que le changement de pente soient le même entre la fin d’un segment et le début d’un autre.

La question en suspens reste, évidemment, combien de noeuds on utilise et où les placer. La chose importante à comprendre est que l’on ne choisit pas directement le nombre de noeuds. On choisit plutôt un paramètre (k), qui contrôle le nombre de degrés de liberté maximum que pourra utiliser notre courbe, i.e. le nombre de petites fonctions (basis function) qu’il pourra connecter ensemble pour former l’entièreté de la courbe. Puisqu’une fonction d’optimisation sera utilisée pour optimiser la courbe, la valeur de k est un plafond de complexité. Il ne sera pas nécessairement utilisé en entier. Si on ne mentionne rien, mgcv utilise k=10, ce qui, pour un maximum de k-1 degrés de liberté en permettra ici 9.

Voyons à quoi pourrait ressembler un spline de régression cubique sur notre jeu de données. On doit emballer pour se faire le terme que l’on veut lisser par la fonction s() et lui spécifier le type de lissage à utiliser (basic function) avec bs="cr" pour obtenir un spline de régression cubique.

Remarquez que l’on doit à nouveau convertir nos dates en jours depuis le 1er janvier 1970 pour la librairie mgcv…

m_c <- gam(chomage_pct ~ s(as.numeric(date), bs = "cr"), data = donnees_chomage)

summary(m_c)


Family: gaussian 
Link function: identity 

Formula:
chomage_pct ~ s(as.numeric(date), bs = "cr")

Parametric coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  3.04007    0.01112   273.3   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Approximate significance of smooth terms:
                      edf Ref.df     F p-value    
s(as.numeric(date)) 8.989      9 482.4  <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

R-sq.(adj) =  0.933   Deviance explained = 93.5%
GCV = 0.040125  Scale est. = 0.038849  n = 314

On voit dans ces sorties que le modèle est extrêmement bien ajusté à nos données (deviance expliquée de 93.5%) et que la courbe sélectionnée utilise 8.89 degrés de libertés.

Enfin, on peut voir que notre modèle a été optimisé en se basant sur le GCV score (generalized cross-validation). Le GCV s’interprète exactement comme une mesure de validation croisée (i.e. une erreur moyenne), mais il exploite certaines propriétés mathématiques pour calculer cette erreur moyenne sans ajuster n-1 modèles différents.

On peut visualiser cette courbe, encore une fois, à l’aide de la fonction predict :

fond_graphique +
  geom_line(
    data = donnees_chomage %>% mutate(prediction = predict(m_c)),
    aes(y = prediction),
    linetype = "dashed",
    color = "blue"
  )

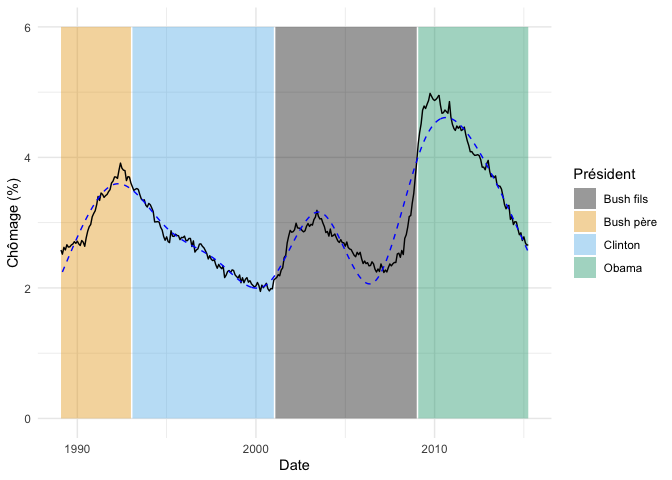
Si on avait voulu obtenir une courbe plus ajustée à nos données, deux options s’offrent à nous.

Tout d’abord, on aurait pu augmenter la valeur de k. Notre modèle utilise 8.89 des 9 degrés de libertés permis, donc possible qu’il ait plafonné. De plus, Simon Wood explique dans son livre que la valeur de k change aussi l’espace de paramètres recherché, et donc qu’augmenter la valeur de k pourrait permettre des solutions plus complexes, même si le nombre de degrés de liberté maximum n’a pas été atteint.

On peut par exemple regarder l’effet d’un doublement de k :

m_c20 <- gam(chomage_pct ~ s(as.numeric(date), bs = "cr", k = 20), data = donnees_chomage)
summary(m_c20)


Family: gaussian 
Link function: identity 

Formula:
chomage_pct ~ s(as.numeric(date), bs = "cr", k = 20)

Parametric coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept) 3.040073   0.004749   640.2   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Approximate significance of smooth terms:
                      edf Ref.df    F p-value    
s(as.numeric(date)) 18.91     19 1327  <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

R-sq.(adj) =  0.988   Deviance explained = 98.8%
GCV = 0.0075608  Scale est. = 0.0070814  n = 314

fond_graphique +
  geom_line(
    data = donnees_chomage %>% mutate(prediction = predict(m_c20)),
    aes(y = prediction),
    linetype = "dashed",
    color = "blue"
  )

Notre courbe épouse encore plus fortement nos données et utilise deux fois plus de degrés de liberté (18.91 vs. 8.9). Selon le GCV score, ce modèle est encore meilleur que le précédent. Cependant, comme il s’agit d’une série temporelle avec beaucoup d’auto-corrélation, la validation croisée n’est peut-être pas le meilleur outil pour évaluer cet ajustement.

Alternativement, on aura pu demander à mgcv d’optimiser le modèle non pas sur le GCV, mais avec un critère basé sur la vraisemblance, par exemple avec le REML :

m_c_reml <- gam(chomage_pct ~ s(as.numeric(date), bs = "cr"), data = donnees_chomage, method = "REML")

summary(m_c_reml)


Family: gaussian 
Link function: identity 

Formula:
chomage_pct ~ s(as.numeric(date), bs = "cr")

Parametric coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  3.04007    0.01112   273.3   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Approximate significance of smooth terms:
                      edf Ref.df     F p-value    
s(as.numeric(date)) 8.974      9 481.7  <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

R-sq.(adj) =  0.933   Deviance explained = 93.5%
-REML = -30.892  Scale est. = 0.038853  n = 314

fond_graphique +
  geom_line(
    data = donnees_chomage %>% mutate(prediction = predict(m_c_reml)),
    aes(y = prediction),
    linetype = "dashed",
    color = "blue"
  )

Ici, notre modèle est presque identique au premier. Cependant, selon plusieurs sources, le GCV aurait tendance à produire des modèles surajustés aux données et le REML serait donc souvent préférable. Le REML serait aussi probablement plus robuste aux données aberrantes.

Enfin, même si ce n’est pas nécessairement recommandé, on peut choisir manuellement les noeuds utilisés par l’algorithme, pour autant que le nombre de noeuds n’entre pas en conflit avec la valeur de k. On aurait par exemple pu décider de mettre un noeud à chaque changement de président.

Ce qui équivaudrait à ce que le taux de chômage soit ajusté par une polynomiale cubique pour chaque président, en ajoutant bien sûr la contrainte que continuité au niveau des noeuds.

noeuds <- c("1989-03-01","1993-01-20","2001-01-20","2009-01-20","2015-04-01") %>% 
  as_date %>% 
  as.numeric

m_c_noeuds <- gam(
  chomage_pct ~ s(as.numeric(date), bs = "cr", k = length(noeuds)),
  knots = list(date = noeuds), 
  data = donnees_chomage, 
  method = "REML"
)

summary(m_c_noeuds)


Family: gaussian 
Link function: identity 

Formula:
chomage_pct ~ s(as.numeric(date), bs = "cr", k = length(noeuds))

Parametric coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)   3.0401     0.0293   103.8   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Approximate significance of smooth terms:
                      edf Ref.df     F p-value    
s(as.numeric(date)) 3.969  3.999 89.06  <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

R-sq.(adj) =  0.533   Deviance explained = 53.9%
-REML = 250.92  Scale est. = 0.26958   n = 314

fond_graphique +
  geom_line(
    data = donnees_chomage %>% mutate(prediction = predict(m_c_noeuds)),
    aes(y = prediction),
    linetype = "dashed",
    color = "blue"
  )

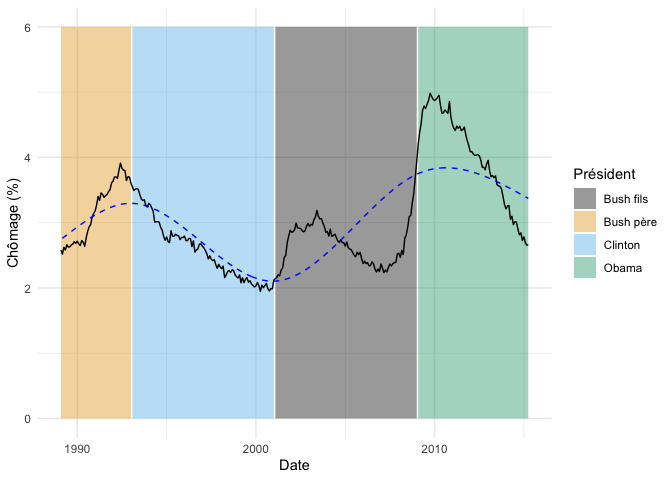
On voit dans ces résultats que ce n’est pas fameux, puisque les changements majeurs de taux de chômage ne coïncident pas nécessairement avec les changements de président. La contrainte de continuité est particulièrement frappante pour le mandat de Bush fils.

Splines de régression à plaques minces

Les splines de régression à plaques minces (thin plate regression splines, TPRS) utilisent une approche complètement différente, où l’idée de segments ou de noeuds est complètement abandonnée.

Dans les TPRS, chaque point possède une zone d’influence (radial basis function, RBF), qui diminue avec la distance par rapport au point. La courbe de lissage sera le résultat de la combinaison de chacune de ces zones d’influence. L’image qui est souvent employée est celle d’une mince feuille de métal déposée sur une série d’objets de différentes grandeurs (d’où le terme à plaques minces).

Plutôt que d’avoir une contrainte à chaque noeud pour que les transitions soient lissent, les TPRS ont plutôt une contrainte globale, qui impose une niveau de lissage total sur la courbe.

Il y a, évidemment, beaucoup de travail d’optimisation derrière ces fonctions pour simplifier la combinaison de RBF en quelque chose qui peut être traité dans un temps raisonnable. Cependant, les TPRS demeurent plus lents à exécuter que les splines de régression cubiques, donc c’est à garder en tête si le temps d’ajustement d’un modèle commence à devenir problématique pour votre projet.

Dans mgcv, un lissage de type TPRS peut être spécifié avec bs="tp" à notre terme de lissage :

m_tp <- gam(
  chomage_pct ~ s(as.numeric(date), bs = "tp"),
  data = donnees_chomage, 
  method = "REML"
)

summary(m_tp)


Family: gaussian 
Link function: identity 

Formula:
chomage_pct ~ s(as.numeric(date), bs = "tp")

Parametric coefficients:
            Estimate Std. Error t value Pr(>|t|)    
(Intercept)  3.04007    0.01067     285   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Approximate significance of smooth terms:
                      edf Ref.df   F p-value    
s(as.numeric(date)) 8.976      9 527  <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

R-sq.(adj) =  0.938   Deviance explained =   94%
-REML = -42.514  Scale est. = 0.035725  n = 314

fond_graphique +
  geom_line(
    data = donnees_chomage %>% mutate(prediction = predict(m_tp)),
    aes(y = prediction),
    linetype = "dashed", 
    color = "blue"
  )

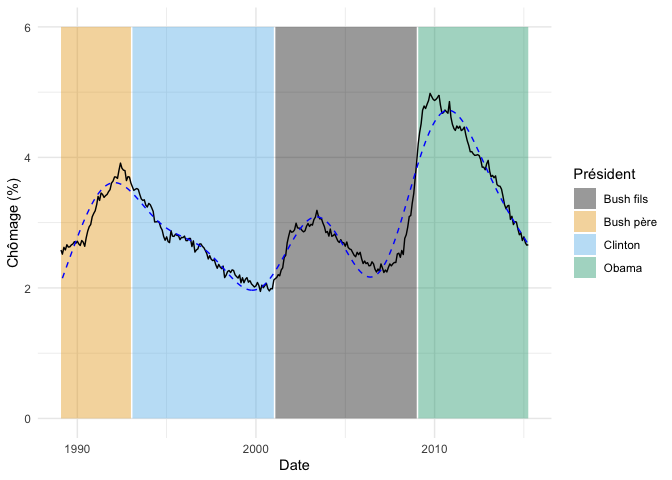
Les lissages de type TPRS, tout comme les splines de régression, peuvent être contrôlés à l’aide d’un paramètre fournit à la fonction. Dans le cas des TPRS, le paramètre se nomme m. Ce dernier contrôle la dimensionalité des zones d’influence. Plus ce chiffre est élevé, plus la courbe aura de liberté pour se tortiller. La valeur par défaut est de 2.

m_tp_4 <- gam(
  chomage_pct ~ s(as.numeric(date), bs = "tp", m=4),
  data = donnees_chomage, 
  method = "REML"
)

fond_graphique +
  geom_line(
    data = donnees_chomage %>% mutate(prediction = predict(m_tp_4)),
    aes(y = prediction),
    linetype = "dashed",
    color = "blue"
  )

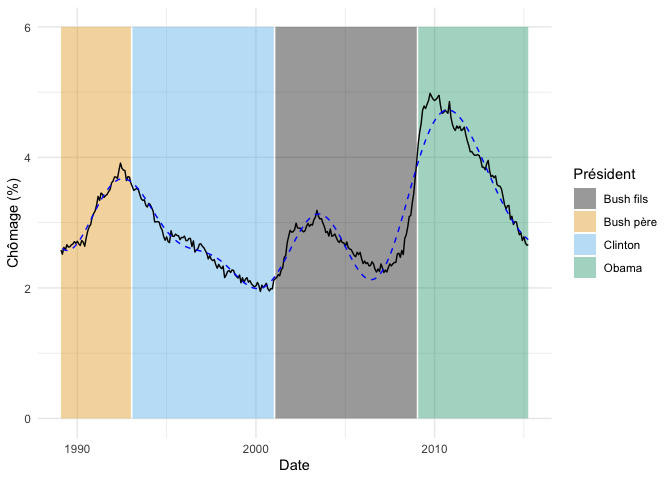
On constate, surtout dans la partie de gauche de la courbe, comme celle-ci épouse mieux les données.

mgcv est extrêmemt flexible

La librairie mgcv est extrêmement flexible. Au-delà des deux types de lissage décrits ci-haut, elle en contient aussi des dizaines d’autres, basés sur une variété d’algorithmes dont nous n’avons pas le temps de discuter ici.

mgcv permet aussi de modéliser l’effet de plusieurs variables différentes dans le même modèle. On peut ajouter les termes comme dans une régression multiple séparés par des +. Les variables peuvent être différents mélanges de relations linéaires, de courbes de lissage et de variables catégoriques.

On pourrait par exemple décider d’ajouter à notre modèle un terme qui tiendrait compte du cycle annuel de chômage, pour aider à discerner l’effet des présidents des effets cycliques.

donnees_chomage <- 
  donnees_chomage %>% 
  mutate(
    jour_de_lannee = yday(date)
  )

donnees_chomage %>% 
  ggplot(aes(jour_de_lannee, chomage_pct)) +
  geom_point()

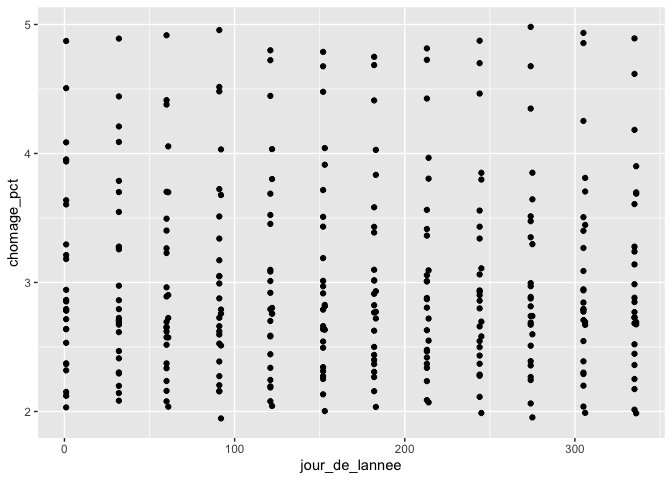
Malheureusement, il n’y a pas de tendance pour le jour de l’année, mais pour l’illustration, nous allons continuer avec ce plan. Remarquez que puisque l’on s’attend à ce que la valeur du 31 décembre et du 1er janvier soient connectées, on peut utiliser un spline cyclique (cc), basé sur le spline cubique, mais auquel on ajoute une contrainte supplémentaire de connecter le premier et le dernier point à la même valeur:

m_multiple <- gam(
  chomage_pct ~ s(as.numeric(date), bs = "tp") + s(jour_de_lannee, bs = "cc"),
  data = donnees_chomage, 
  method = "REML"
)
  
plot(m_multiple)

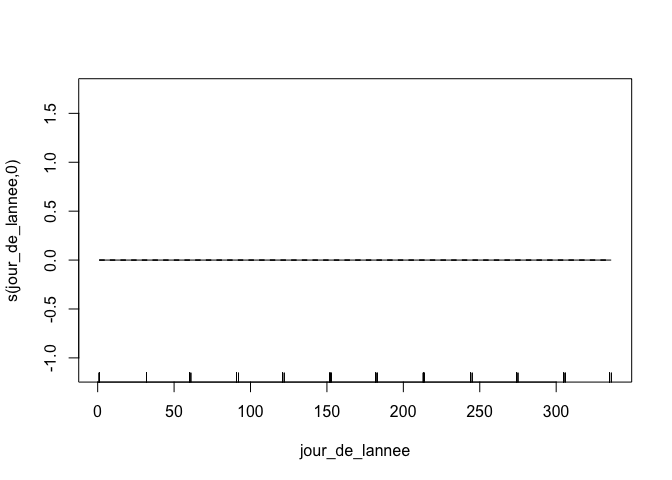
La fonction plot nous permet de visualiser chacun des splines ajustés, indépendamment de l’effet de l’autre. Mais comme discuté plus haut, le jour de l’année ne présente pas vraiment de tendance. mgcva donc simplement ajusté une ligne droite.

La fonction gam de mgcv permet aussi de modifier la famille d’erreur (binomiale négative, beta, etc.) de même que d’ajouter des effets aléatoires.

Si on voulait par exemple utiliser la distribution d’erreur Beta pour prédire le taux de chômage en fonction du jour de l’année en ajoutant une ordonnée à l’origine aléatoire pour l’identité du président, on pourrait écrire ce modèle comme ceci :

donnees_chomage <- 
  donnees_chomage %>% 
  mutate(
    chomage_01 = chomage_pct/100,
    president = as_factor(president)
  )

m_re <- gam(
  chomage_01 ~ s(jour_de_lannee, bs = "cc") + s(president, bs = "re"),
  data = donnees_chomage,
  method = "REML",
  family = betar
)

summary(m_re)


Family: Beta regression(1235.735) 
Link function: logit 

Formula:
chomage_01 ~ s(jour_de_lannee, bs = "cc") + s(president, bs = "re")

Parametric coefficients:
            Estimate Std. Error z value Pr(>|z|)    
(Intercept)  -3.4534     0.1016  -33.98   <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Approximate significance of smooth terms:
                       edf Ref.df Chi.sq p-value    
s(jour_de_lannee) 0.001202      8    0.0   0.866    
s(president)      2.973190      3  410.1  <2e-16 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

R-sq.(adj) =  0.569   Deviance explained = 55.5%
-REML = -1220.3  Scale est. = 1         n = 314

Gamma, une pénalité globale pour ajuster le lissage de tout le modèle

Nous avons vu que chacun des termes de lissage peut être ajusté de façon individuelle, soit avec le paramètre k pour les splines de régression cubique et m pour les TPRS. Dans tous les calculs, mgcv applique aussi une pénalité globale, avec un paramètre nommé gamma. Plus gamma est élevé, plus il sera coûteux de courber la fonction, la valeur par défaut étant de 1.

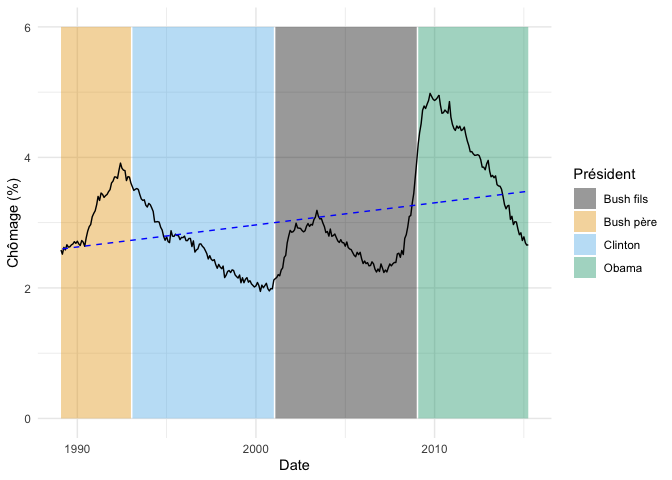
Par exemple, en mettant la pénalité 50x plus grande, il devient tellement coûteux de courber la fonction que gam passe simplement une fonction linéaire à travers nos données :

m_tp_gamma <- gam(
  chomage_pct ~ s(as.numeric(date), bs = "tp"),
  data = donnees_chomage, 
  method = "REML",
  gamma = 50
)

fond_graphique +
  geom_line(
    data = donnees_chomage %>% mutate(prediction = predict(m_tp_gamma)),
    aes(y = prediction),
    linetype = "dashed",
    color = "blue"
  )

Conclusion

Donc, si on résume, il existe une série d’outils différents permettant de modéliser des phénomènes non linéaires, soit :

Et dans presque tous les cas, il est nécessaire d’exercer notre jugement dans le choix des pénalités imposées aux modèles, puisque celles-ci (1) sont arbitraires et (2) elles peuvent avoir un impact important sur le résultat final du modèle.

Références

Pour un aperçu de l’ensemble des méthodes non linéaires, je vous conseille le chapitre 7 (Moving Beyond Linearity) de An Introduction to Statistical Learning with Applications in R, de James et al. (2013).

Si une méthode vous intéresse en particulier, je vous conseille les articles présentant les différentes librairies soit :

Et enfin, si vous voulez vraiment avoir l’ensemble des détails, rien ne remplace le livre de Simon N. Wood : Generalized additive models: An introduction with R. Second Edition (2017)