PARAFAC Duetta
Jessika Malko, validé par Jade Dormoy-Boulanger
Mai 2025
Vous pouvez vous procurer le code R ainsi qu’un échantillon d’EEMs avec lesquels vous amuser au lien suivant: https://numerilab.io/assets/Duetta/AtelierDuetta.zip
D’autres ressources intéressantes sont :
- l’article de Murphy et al., 2013 qui explique la méthode PARAFAC https://pubs.rsc.org/en/content/articlelanding/2013/ay/c3ay41160e
- et le tutoriel de Matthias Pucher qui a écrit le package staRdom basé sur la méthode de Murphy et al. https://cran.r-project.org/web/packages/staRdom/vignettes/PARAFAC_analysis_of_EEM.html
Un peu de théorie…
L’analyse PARAFAC est basée sur la spectroscopie, soit l’étude de l’absorption et de l’émission de la lumière par la matière.
Le PARAFAC est de plus en plus utilisé depuis une 20aines d’années pour qualifier la composition chimique des matières organiques dissoute (MOD) dans l’environnement. La fluorescence fournit une matrice en 3 dimensions (EEM) qui mesure l’intensité de l’excitation et de l’émission d’un échantillon à différentes longueurs d’ondes.
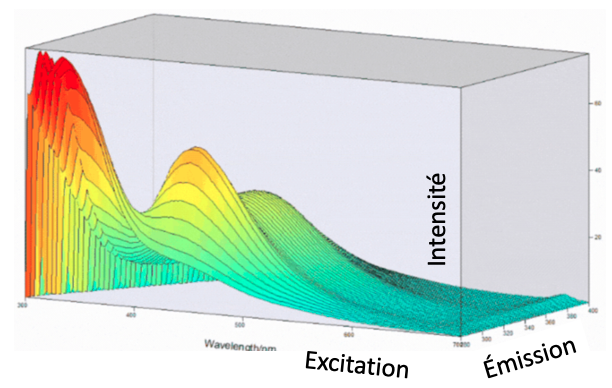
La fluorescence c’est la partie de la lumière qui est émise après qu’elle ait passée au travers de l’échantillon. La lumière absorbée excite les électrons des molécules dans l’échantillon. Quand les électrons retournent à leur état stable, ils réémettent l’énergie en différent sous-produits comme on le voit dans la figure suivante.
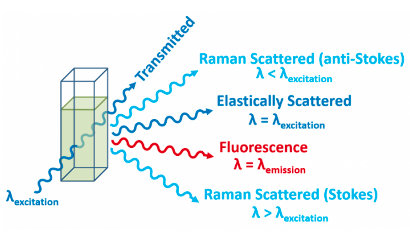
Il y a émission de la fluorescence, en rouge, et il y a aussi l’émission de différents bruits ou « scatter ». Ce bruit nécessite beaucoup de correction pour nettoyer le signal de l’échantillon, c’est l’inconvénient de la spectroscopie.
En sc. environnementales, on s’intéresse à caractériser la composition des matières organiques dissoutes (MOD), car ce sont des molécules bio-réactives qui nourrissent la chaine trophique. La fluorescence est considérée une bonne technique pour ce faire puisqu’il y aurait environs 10 – 30 % des MOD dans l’eau de rivière qui fluorescent. On voit ici une brève liste des molécules qui sont fluorescentes et celles qui ne le sont pas.

Ce sont surtout les matières « humic-like » et « proteic-like » qui fluorescent. La partie de la molécule qui fluoresce s’appelle un fluorophore. Prenons le tryptophane par exemple. L’anneau d’iode qui le compose est le fluorophore et c’est lui qui fait fluorescer la molécule. C’est donc grâce aux différents fluorophores qu’on est capable de constituer une empreinte moléculaire unique en 3 dimensions pour chacun de nos échantillons.

Si on parle d’absorbance maintenant. C’est la partie de la lumière qui est absorbée par les molécules. L’absorbance produit une matrice 2D: en X on a les longueurs d’ondes et en Y l’intensité. C’est l’absorbance qui nous permet de corriger pour le Inner Filter Effect (IFE). Pour faute de temps, je vous invite à consulter l’article de Murphy et al. 2013 (voir en haut de page pour le lien) pour bien comprendre c’est quoi L’IFE. Il existe aussi des indices qui ont étés développés à partir des longueurs d’ondes d’absorbance : comme le poids moléculaire (Sr) et le SUVA qui nous informe indirectement sur la source de la molécule (microbien ou végétal) en fonction de son aromaticité.
Il existe aussi des indices dérivés de longueurs d’ondes de la fluorescence. Sachez cependant qu’au début de l’année, un article est sorti par Serène et al. qui questionnent les coordonnées de longuers d’ondes utilisées pour obtenir ces indices. Systématiquement appliqués à différents projets, Serène et al. on trouvé que les coordonnées utilisées pour inférer les indices doivent être corrigées et adaptées pour chaque milieu car ils changeraient même d’un océan à l’autre. Je vous invite à lire l’article pour plus de détails : https://doi.org/10.1016/j.jhydrol.2024.132524. Si vous tenez tout de même à calculer vos indices, je vous invite à l’atelier qui a déjà été réalisé par Jade et Mathieu et qui est disponible sur le site web du Numérilab.
Tel que mentionné, le PARAFAC est une méthode d’analyse multidimensionnelle. Notre jeu de donné est composé d’EEMs (matrice d’excitation et d’émission). L’analyse nous permet d’analyser cet assemblage et de décomposer le signal des échantillons pour en faire ressortir les différentes composantes (PEAKs ou « hotspots ») caractéristiques de notre jeu de données.

Le nombre de composantes va varier en fonction de notre projet et du soin qu’on apporte à la construction de notre modèle. Prenons le PEAK B-T encadré en rouge dans l’image ci-dessous. Si le signal est suffisamment nuancé dans l’ensemble de nos échantillons, nous sommes capables de le décomposer davantage : le tyrosine (ex 275, em 345), le tryptophane (ex 270, em 300) et les phénols (ex 260, em 280).

Ci-dessous, dans l’image de gauche, on voit que la matrice EEM peut être séparée en 5 régions. Ces régions, ou PEAKs, sont les plus communes et ont été identifiées comme suit:
- Le PEAK A en jaune et C en bleu : identifient une source terrestre humique. Ils fluorescent souvent en même temps comme on peut le voir dans la C1 juste à droite.
- Le PEAK B et T en noir : identifient une source protéique-like, comme on vient de le voir avec l’exemple du tryptophane et de la tyrosine. Ces acides aminées sont dérivées de la dégradation de la MOD et sont représentés par la C2.
- Le PEAK X en orange : est une autre forme de signature humique terrestre comme on le voit par la C3.
- Le PEAK A en jaune : est encore une fois une autre forme de matières humiques, ici identifiées comme ayant une source terrestre ou agricole et qui est représenté par la composante C4.
- Le PEAK M en bleu : identifie une activité microbienne et est représenté par la composante C5.
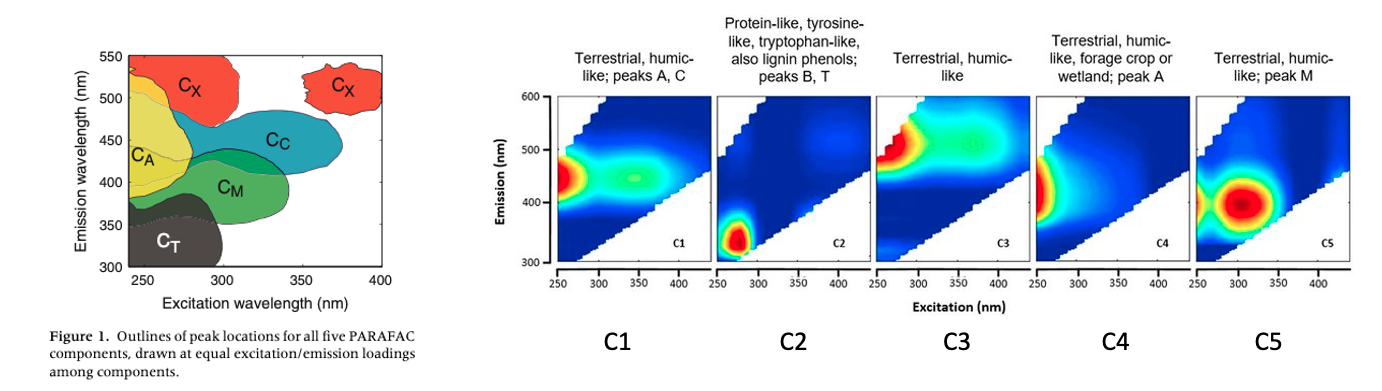
La numérotation des composantes (C1, C2, …) est aléatoire et dépends du modèle. Dans Mathlab, le modèle classe les composantes en fonction de leur importance alors que dans staRdom, l’attribution semble aléatoire. Ainsi, lorsque vous allez comparer votre modèle à la base de données Open Fluor, votre C1 pourrait correspondre au C3 du modèle d’un autre chercheur.

L’instrument Duetta marque une nouvelle ère dans la spectroscopie. Vantée comme étant le spectromètre « le plus rapide sur le marché », la Duetta permet de faire l’acquisition de l’absorbance et de la fluorescence en même temps! L’instrument permet aussi de contrôler le temps d’intégration (le temps du scan pour chaque longueurs d’ondes dont le range va de 0.05 à 6.0 secondes / wl) des échantillons. L’avantage c’est d’avoir une meilleure résolution de nos EEMs, l’inconvénient c’est qu’il faut savoir ‘calibrer’ la machine à nos échnatillons pour en tirer profit! Ce n’est pas tout, la Duetta corrige pour tous les types d’erreurs sauf une: le bruit du 1erordre de Rayleigh.
- Point clef : bâtir un modèle PARAFAC est une méthode itérative et sujette à interprétation. Avec les échantillons d’EEMs fournit, vous allez voir qu’on est capable de produire un modèle qui « passe » les tests mais qui ne serait pas bien reçu par vos pairs. Je vais vous montrer comment identifier les indices pour parvenir à créer un modèle que vous pourrez appliquer à l’ensemble de vos échantillons.
L’atelier
Débutons! Installez d’abord le package et activez les librairies.
# install.packages("staRdom")
library(dplyr)
library(tidyr)
library(ggplot2)
library(staRdom) # la version Github est mise à jour plus rapidement
Détectons le nombre de coeurs que possède notre ordinateur. Ceci nous permettra de maximiser la puissance de calcul de certaines fonctions plus loin.
cores <- detectCores(logical=FALSE) # j'ai 12 coeurs
Importation des données
Nous sommes prêts à importer notre jeu de données, nos EEMs. Assurez-vous que le dossier “fluo” soit dans le même répertoire de travail que votre projet.
EEM <- eem_read("fluo", import_function = "aqualog")
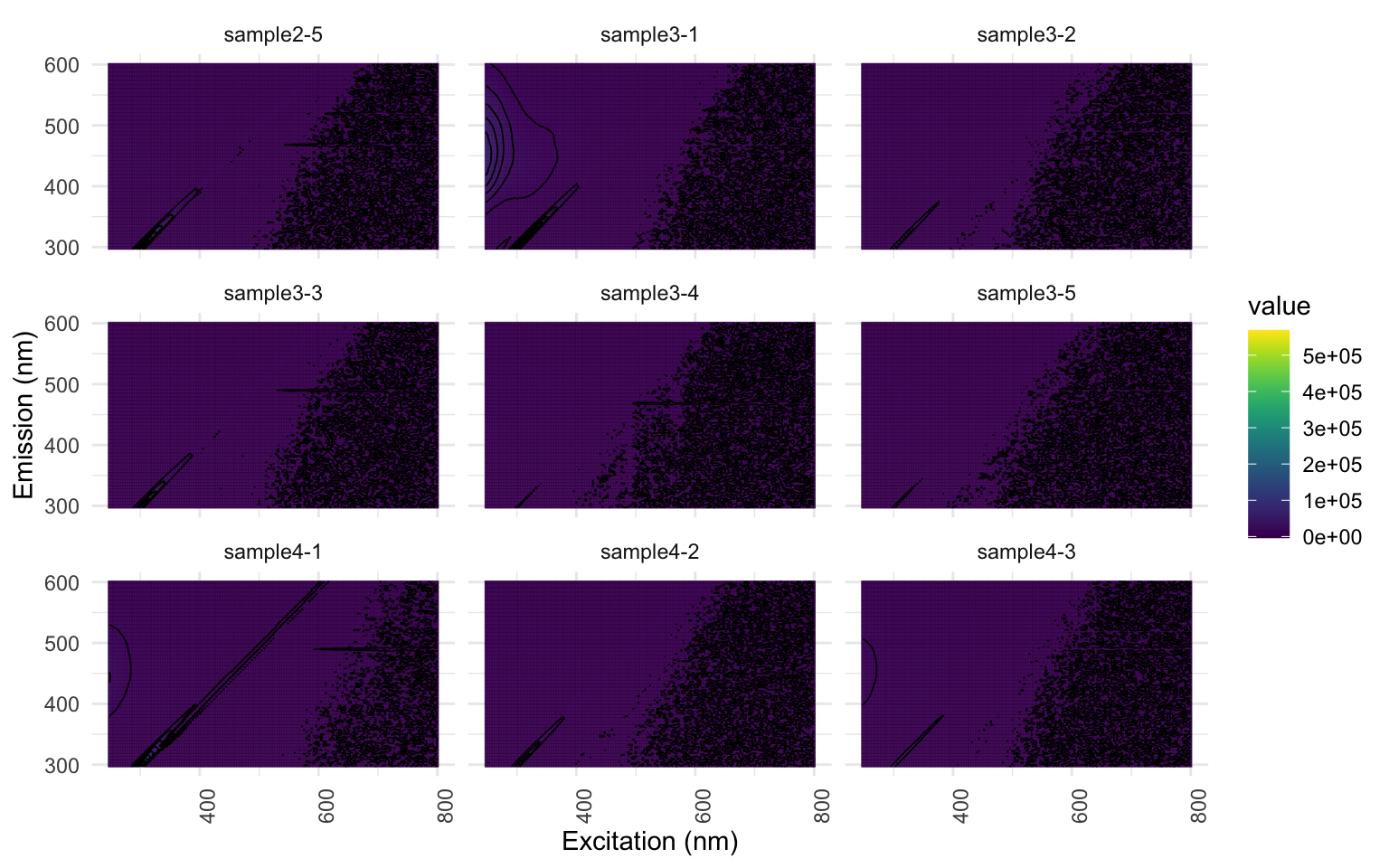
Nous pouvons visualiser nos EEMs, échantillon par échantillon, pour faire un premier survol visuel des données avec lesquels nous travaillerons. Je recommande plutôt de regrouper le nombre d’échantillons affichés par page, ici 9 par page (spp=9). À ce stade, c’est normal que le résultat ne montre que des carrés bleu/mauve foncés. Portez une attention particulière aux axes. Ici, les longueurs d’ondes pour l’excitation sont en X et les émissions en Y. Les axes sont parfois inversés dans la littérature.
eem_overview_plot(EEM, spp=9, contour = TRUE)
[[1]]
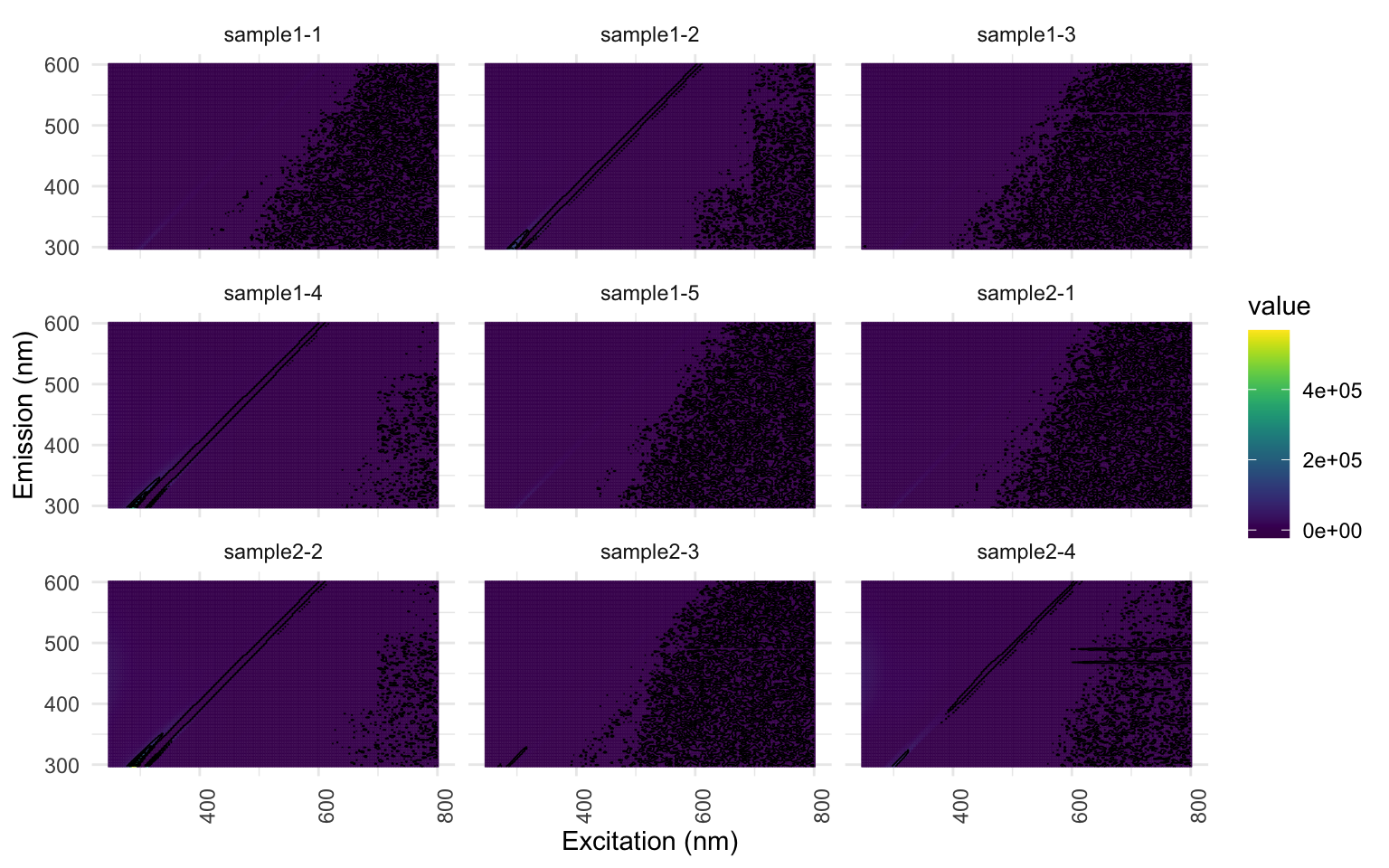
[[2]]
[[3]]
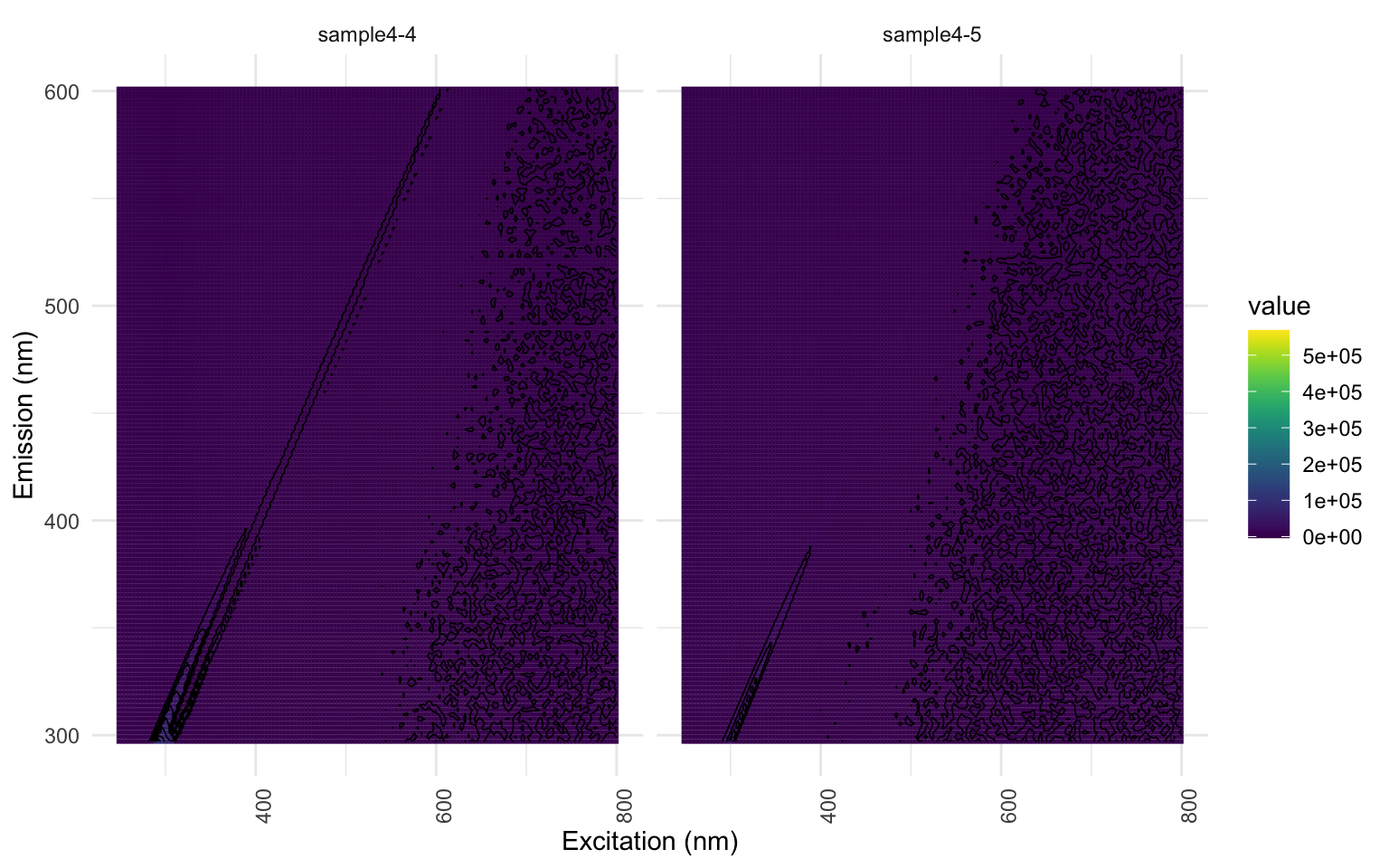
Puisque nous nous intéressons uniquement à une portion des longueurs d’ondes incluses, nous allons découper nos EEMs pour recadrer nos résultats dans la zone d’intérêt. De ce que j’ai pu voir jusqu’à présent, cette zone est plutôt universelle d’une étude à l’autre. Ce découpage permet également d’accélérer le rendu.
EEM <- eem_range(EEM, ex = c(250,500), em = c(0,600))
Corrections des EEMs
Tel que mentionné, l’instrument Duetta produit des EEMs déjà corrigés sauf pour le bruit causé par le 1er ordre de Rayleigh. Le processus de correction est itératif. Je vous recommande de commencer avec une petite valeur (5), et d’augmenter progressivement jusqu’à l’élimination (presque) complète de bruit pour vous assurer que vous ne modéliserez pas d’artéfact par erreur.
remove_scatter <- c(FALSE, FALSE, TRUE, FALSE) # indiquer quel scatter corriger dans l'ordre suivant : RAM1, RAM2, RAY1, RAY2
remove_scatter_width <- c(0,0,20,0) # indiquer la largeur à découper
EEMlist <- eem_rem_scat(EEM, remove_scatter = remove_scatter, remove_scatter_width = remove_scatter_width)
# Le code ci dessous fait la même chose mais sans créer d'objets pour les arguments
# eem_list <- eem_rem_scat(eem_list, remove_scatter = c(FALSE, FALSE, TRUE, FALSE), remove_scatter_width = c(0,0,20,0), interpolation = FALSE, cores = cores)
eem_overview_plot(EEMlist, spp=9, contour = TRUE) # Visualiser le découpage pour s'assurer qu'il soit suffisant
[[1]]
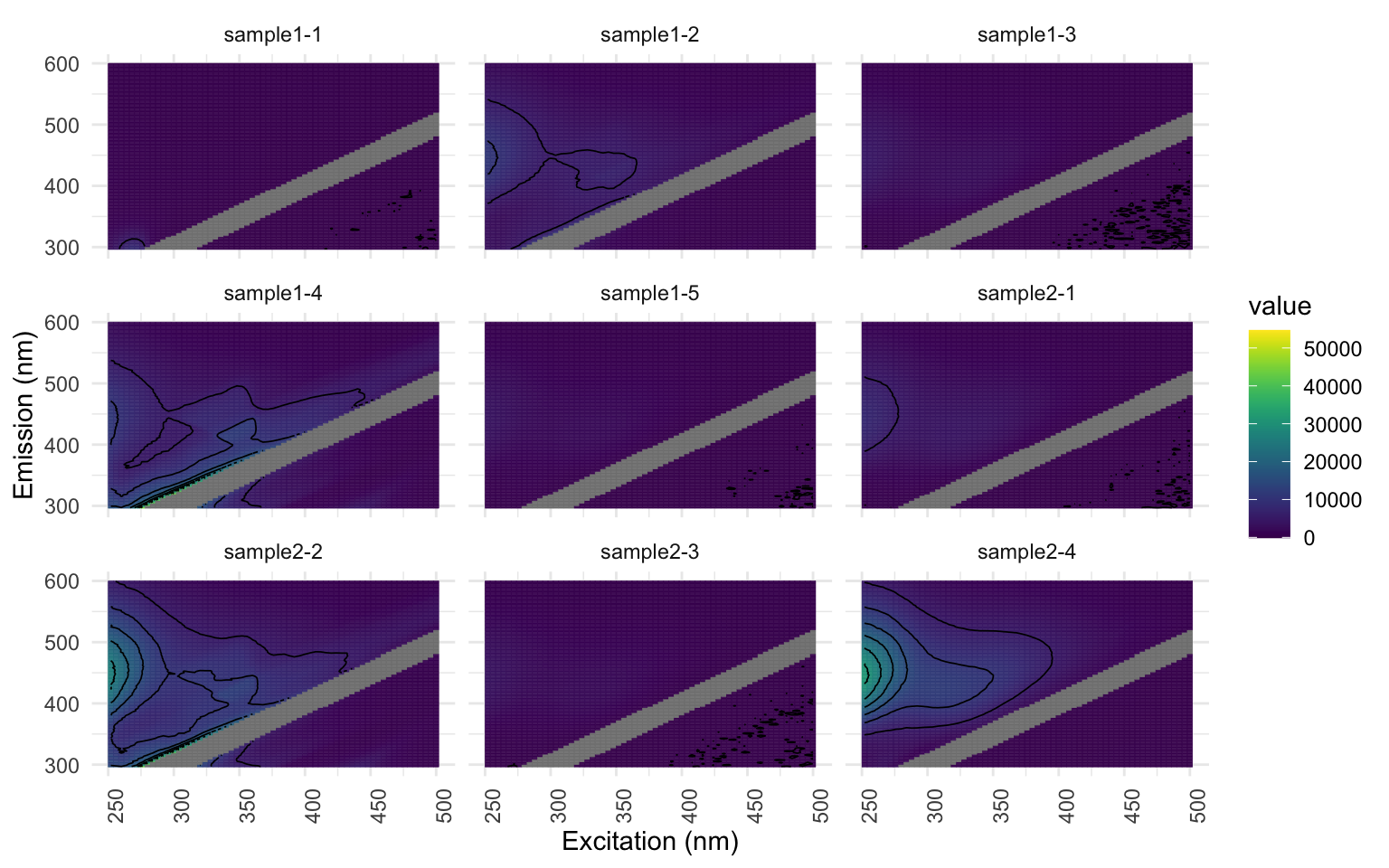
[[2]]
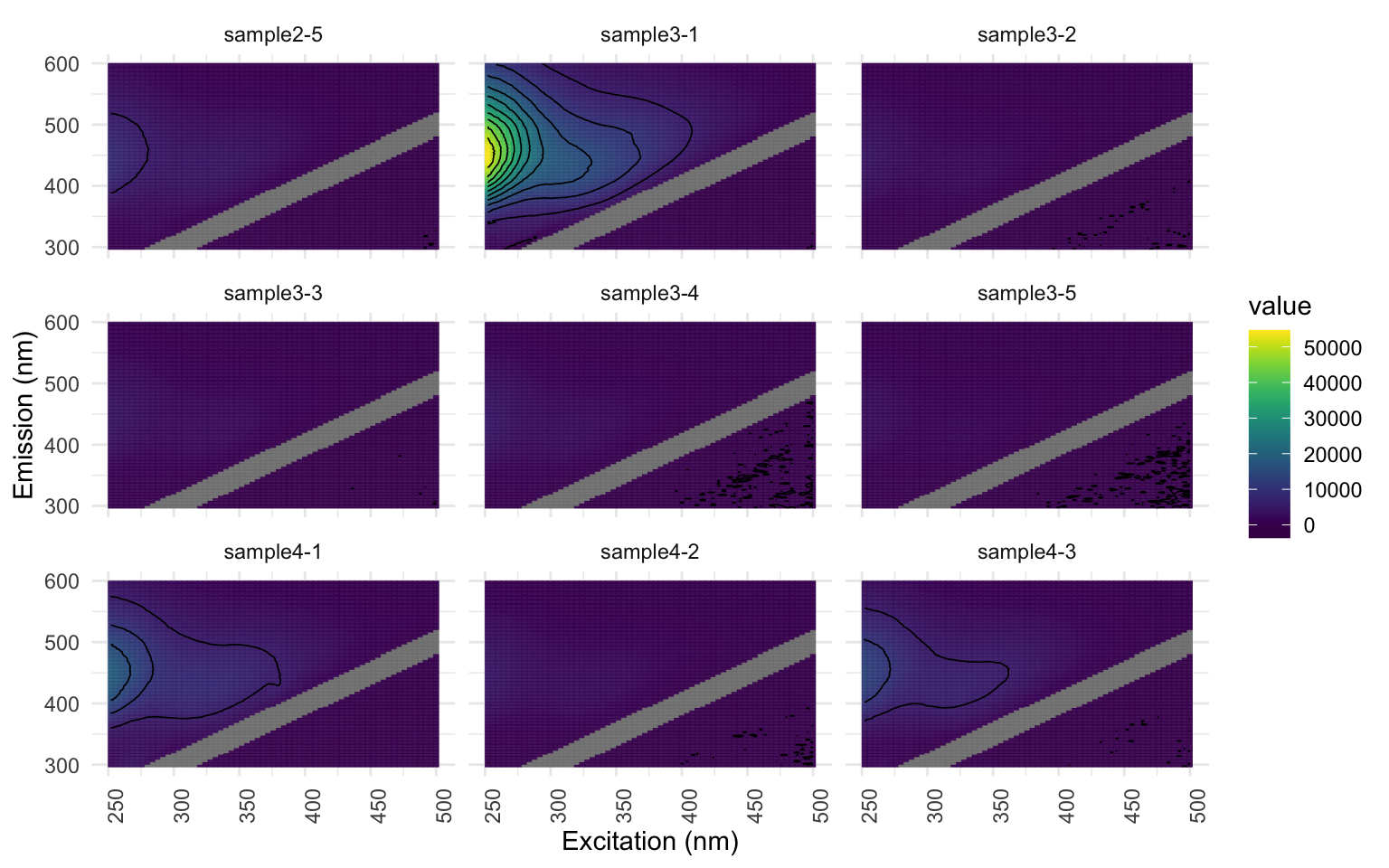
[[3]]
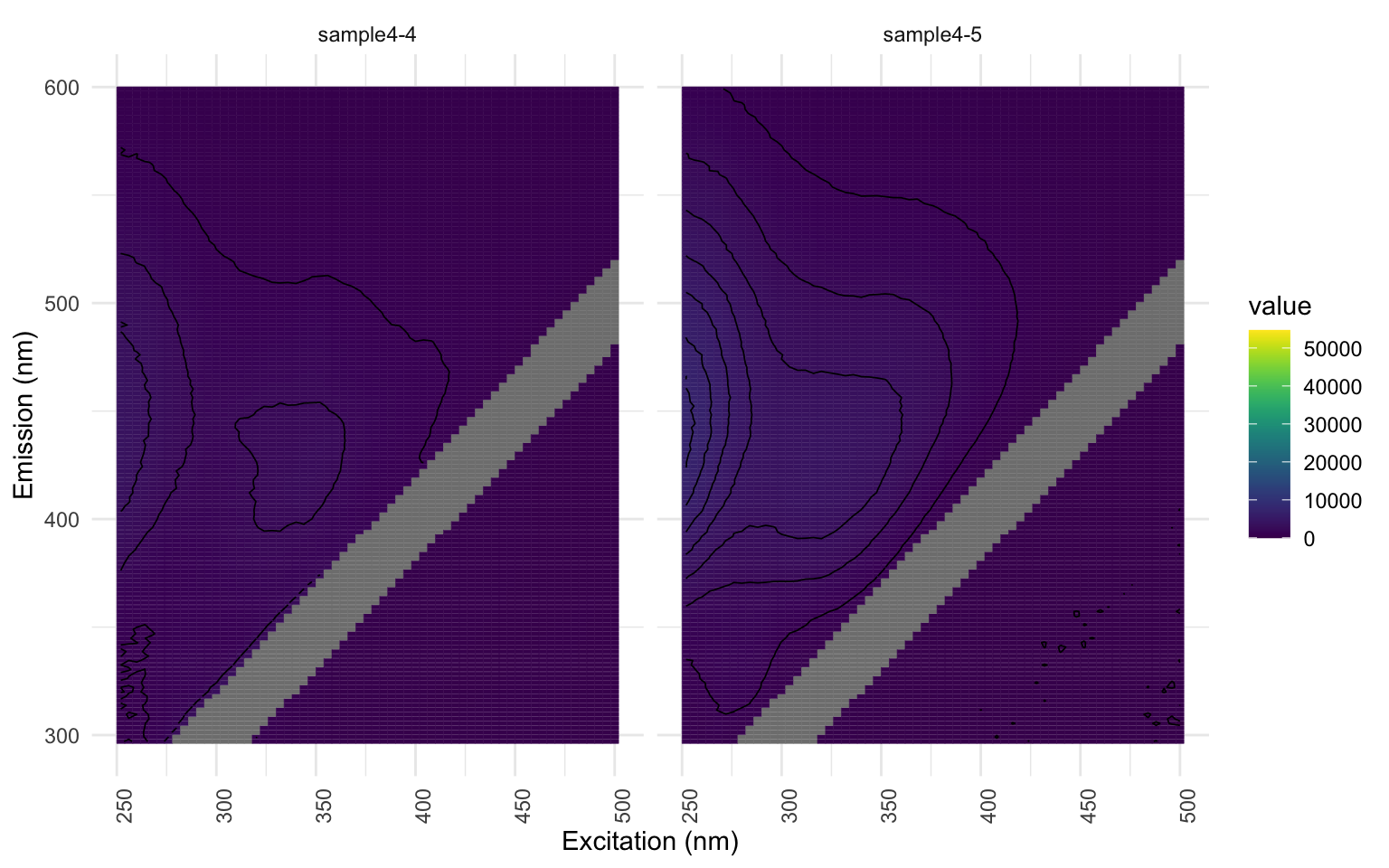
Si vous travaillez avec l’échantillon d’EEMs fournit, vous pourrez constater que même un découpage à une valeur 20 est insuffisant; les échantillons “sample1-2”, “sample1-4”, “sample2-2” et “sample4-4” présentent une coloration jaune au-dessus de la bande découpée. Mais nous le gardons ainsi pour les besoins de l’atelier.
Maintenant que nous sommes satisfais avec le nettoyage de nos EEMs, nous allons procéder à interpoler le ‘vide’ que nous venons de découper. L’interpolation permet de remplir les valeurs manquantes à l’aide d’un procédé mathématique éprouvé dont je vous épargne les détails. Encore une fois, je vous invite fortement à lire l’article de Murphy et al., 2013 disponible au lien suivant : https://pubs.rsc.org/en/content/articlelanding/2013/ay/c3ay41160e.
EEMlist <- eem_interp(EEMlist, cores = cores, type = 4, extend = FALSE)
eem_overview_plot(EEMlist, spp=9, contour = TRUE) # visualisation des EEMs interpolés
[[1]]
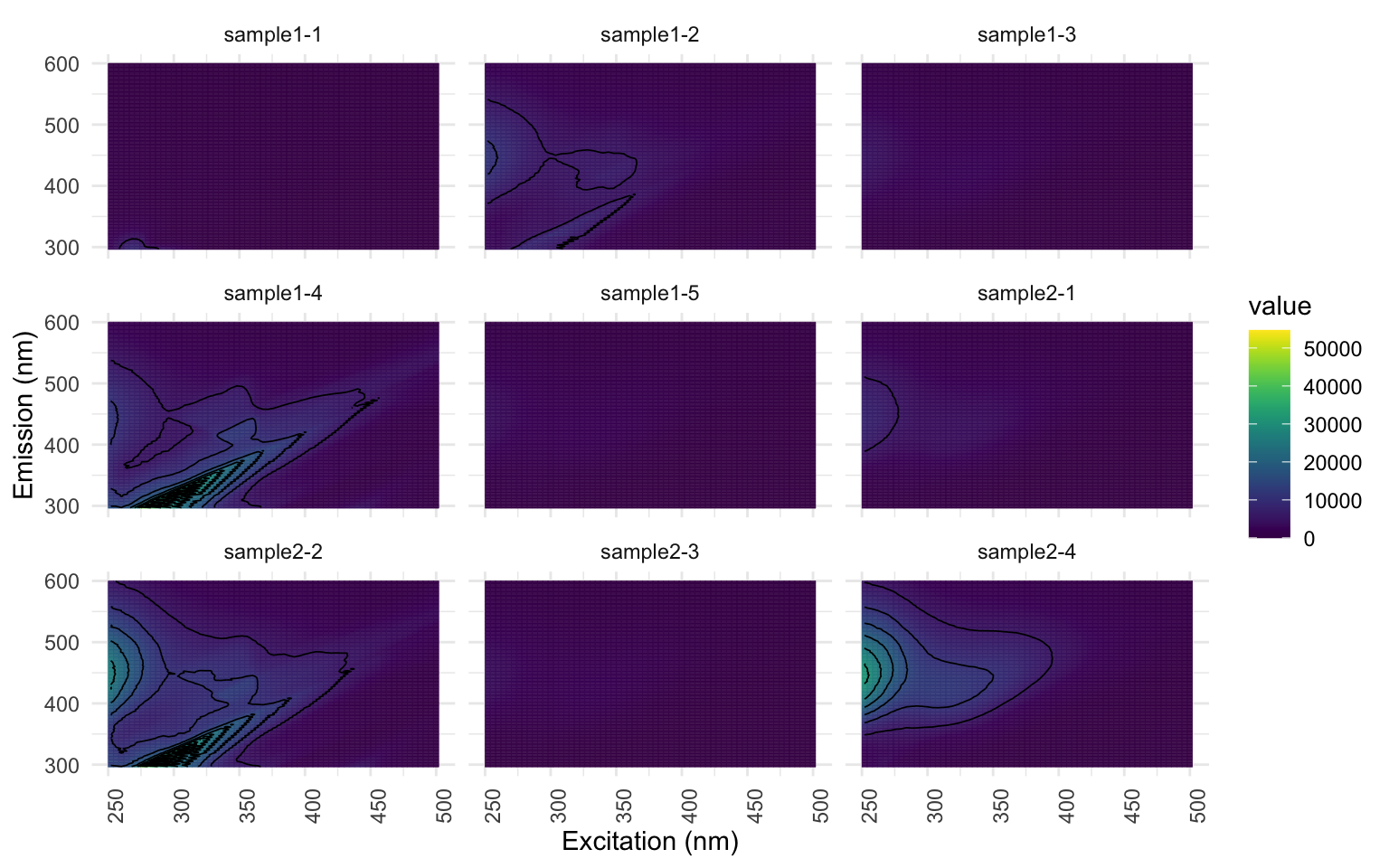
[[2]]
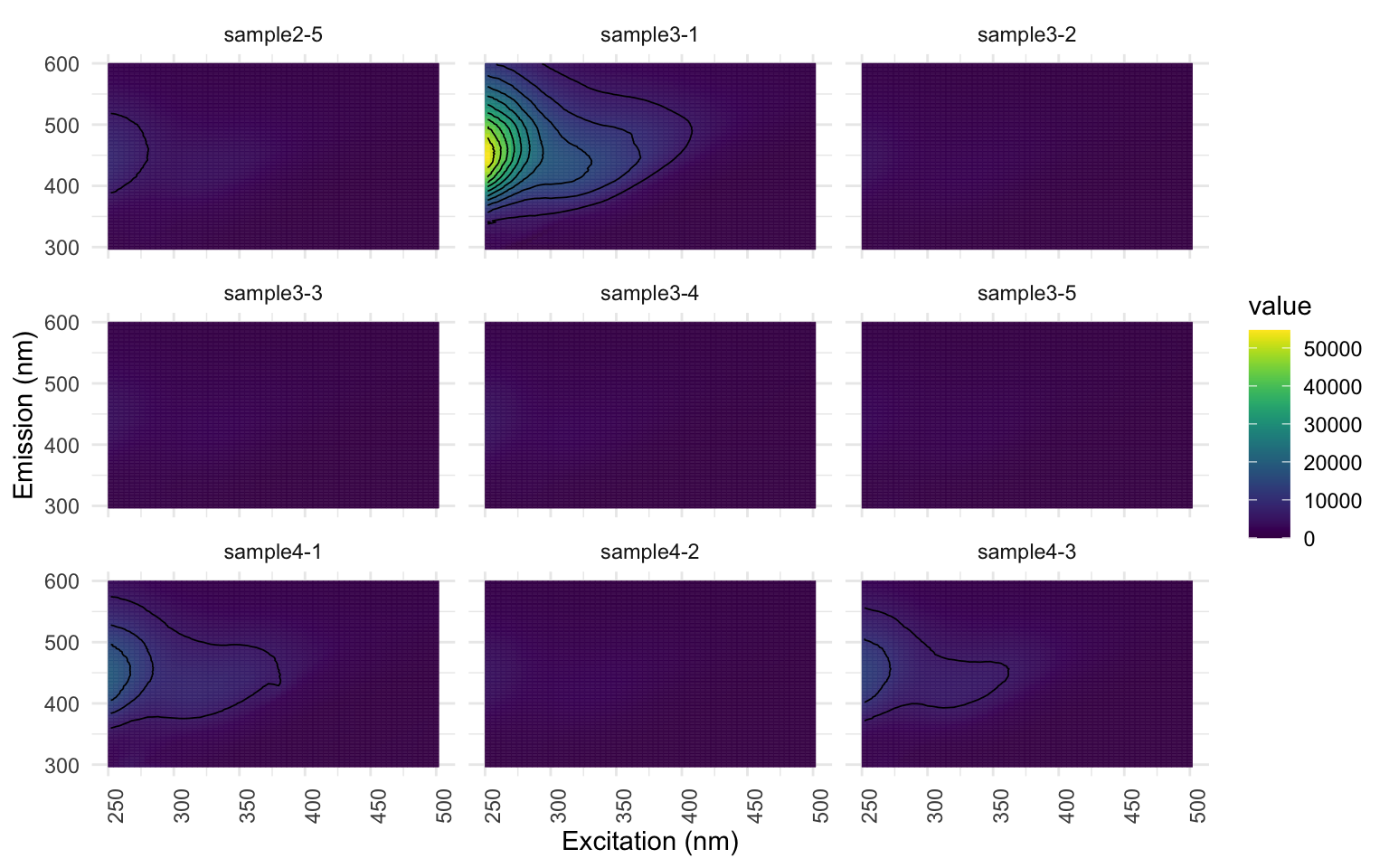
[[3]]
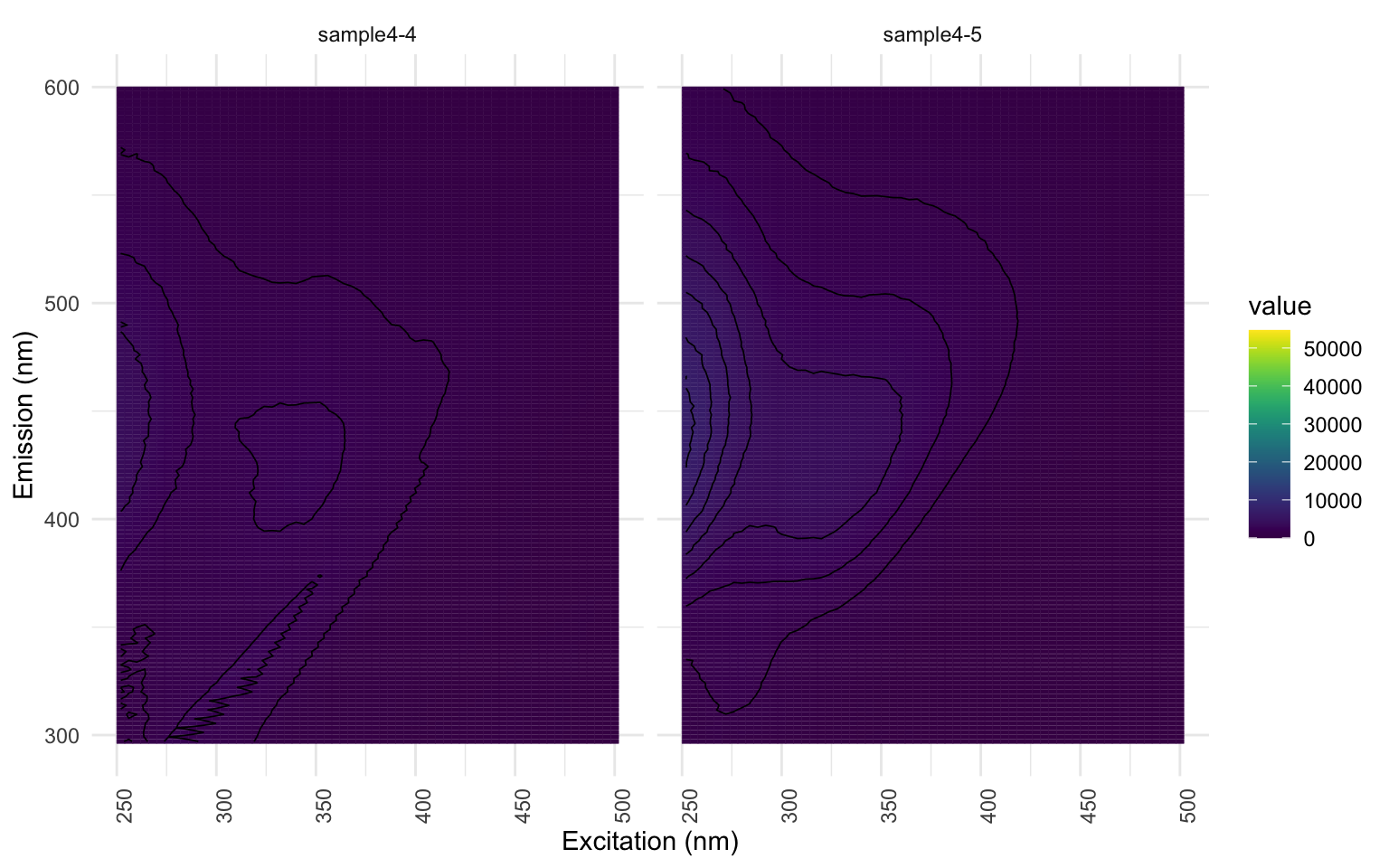
Regardons les échantillons “sample1-2”, “sample1-4”,”sample2-2” et “sample4-4”: notez comment l’interpolation donne un signal relativement fort pour le bruit résiduel que nous avons identifié et choisi de ne pas découper à l’étape précédente. Ceci n’est pas souhaitable. Vous devriez donc retourner à l’étape précédente pour raffiner votre découpage du scatter. Encore une fois, pour les besoins de l’atelier, nous allons poursuivre sans réaliser cette correction. Vous pourriez même choisir d’exclure complètement certains échantillons erratique sur la base visuelle des EEMs (j’ai eu à le faire pour mon projet de maîtrise : certains échantillons étant trop argileux).
Modèle préliminaire
Procédons maintenant à la modélisation. Les valeurs par défaut des variables “nstart”, “maxit” et “ctol” sont un bon point de départ. Il se peut que vous obteniez un message d’erreur qui vous incite à les augmenter afin d’augmenter les chances à un modèle à X-nombre de composantes de converger : “The PARAFAC model with 5 components did not converge! Increasing the number of initialisations (nstart) or iterations (maxit) might solve the problem.” Les valeurs de dimensions minimales et maximales habituelles sont de 3 et 7, respectivement. Un modèle à deux composantes n’est pas très significatif: je l’utilise ici puisque nous avons un très petit nombre d’EEMs. D’autre part, il est très rare que vous aurez à produire un modèle avec plus de 7 composantes; F. Guillemette a eu à le faire lorsqu’il travaillait avec des lixiviats frais en contexte expérimental.
# configuration des paramètres du modèle
dim_min <- 2 # nombre de composantes minimum
dim_max <- 7 # nombre de composantes max
nstart <- 25
maxit = 2000
ctol <- 10^-6 # seuil de tolérance
Sachez qu’il existe différentes contraintes que nous pouvons utiliser pour générer notre modèle. En science de l’environnement, nous utilisons la contrainte non-négative car les éléments des EEMs sont des valeurs positives et aussi parce que les composantes qui découlent de cette contrainte sont celles qui ressembles le plus au spectre fluorescent des fluorophores. Vous pouvez aller voir les autres contraintes avec les code : CMLS::const() si vous êtes curieux.
# modèle qui emplois des contraintes de non-négativité
pf1n <- eem_parafac(EEMlist, comps = seq(dim_min,dim_max),
normalise = FALSE,
const = c("nonneg", "nonneg", "nonneg"),
maxit = maxit,
nstart = nstart,
ctol = ctol,
cores = cores)
On peut redimensionner les valeurs de fluorescence du modèle à 1 pour aider à la lisibilité des graphiques lorsque la hauteur des PEAKs (l’intensité) varie beaucoup. Je vais réutiliser cet argument après chaque modèle pour le reste de l’atelier.
pf1n <- lapply(pf1n, eempf_rescaleBC, newscale = "Fmax")
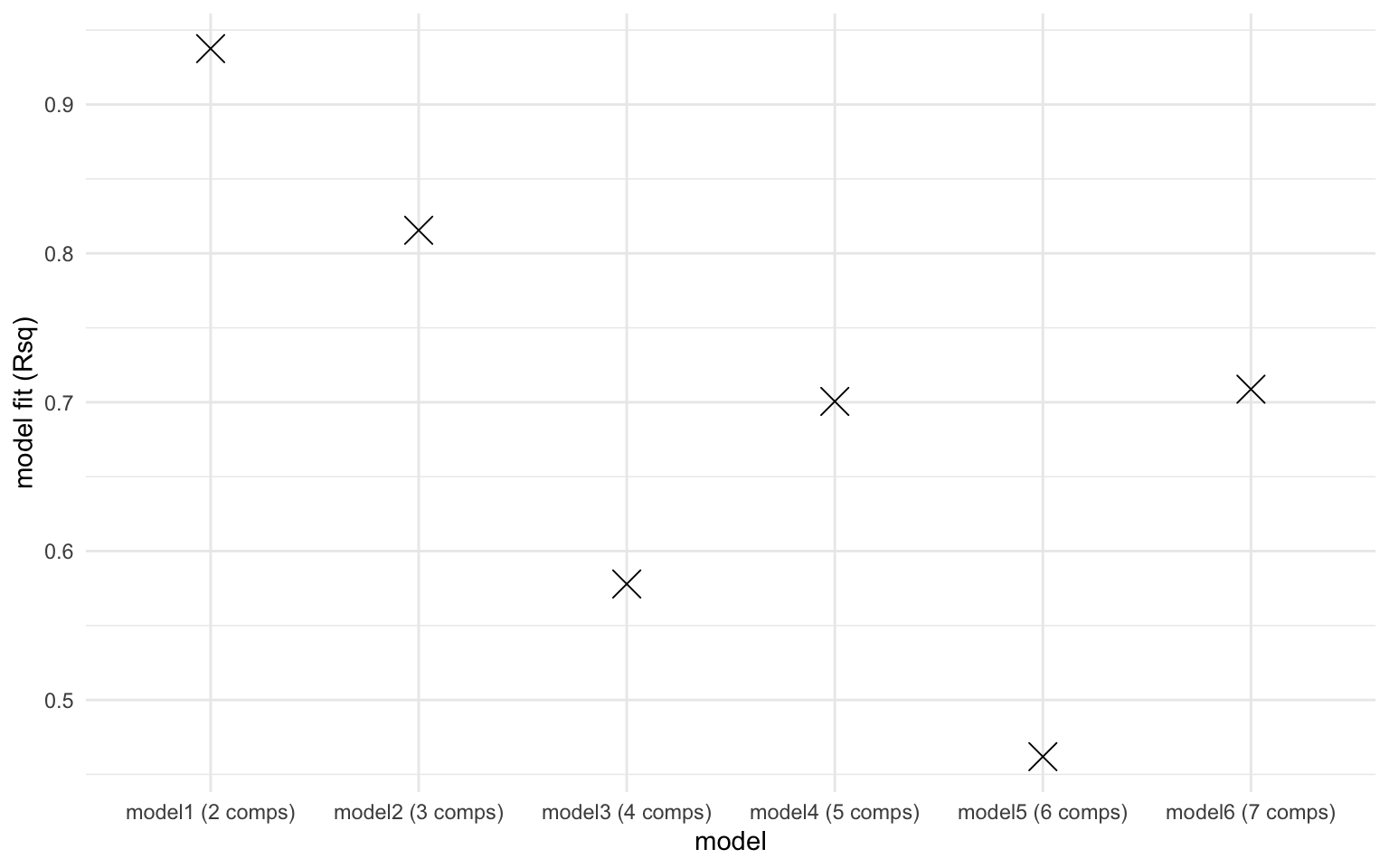
Comparons maintenant les différents nombres de composantes pour nous aider à choisir le meilleur modèle. La fonction emmpf_compare() nous permet de visualiser 3 informations en graphiques : 1) le fit du modèle selon le R2, 2) la représentation visuelle des composantes (vue du dessus) et 3) la représentation visuelle des composante (vue de côté). * Notez que je n’ai pas pris le temps de trouver la façon d’éviter que les graphiques s’affichent en double…*
eempf_compare(pf1n, contour = TRUE)
[[1]]
[[2]]
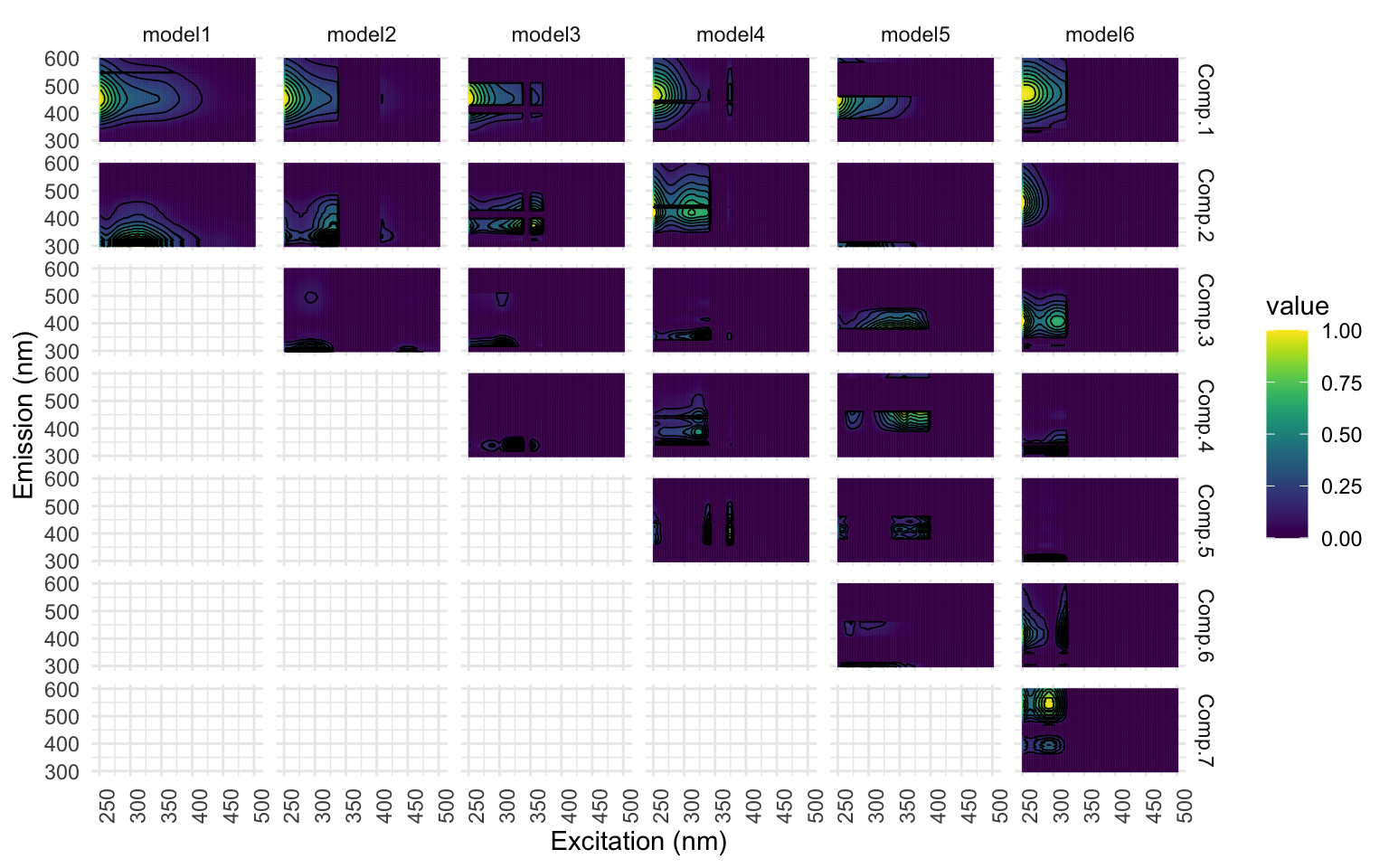
[[3]]
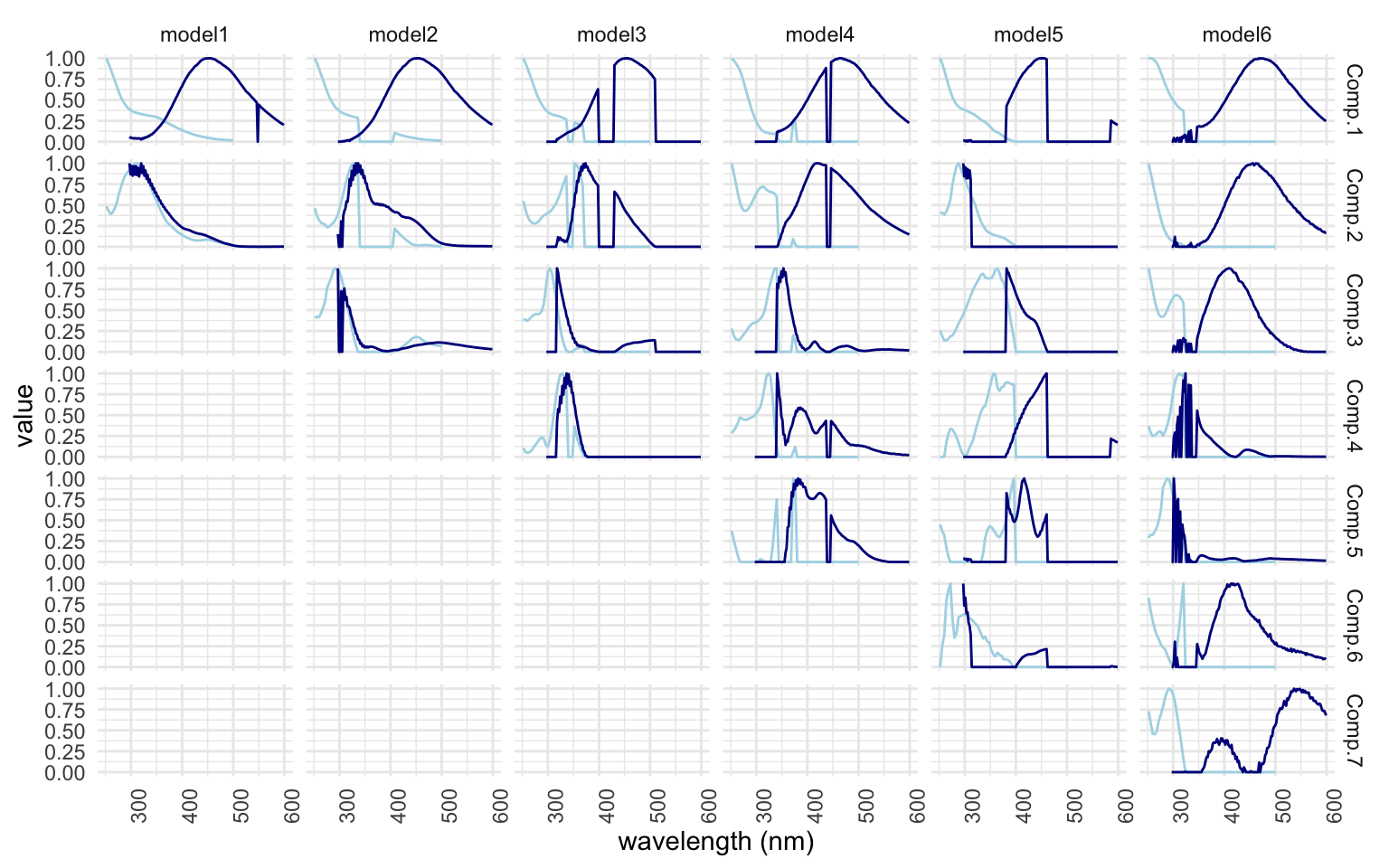
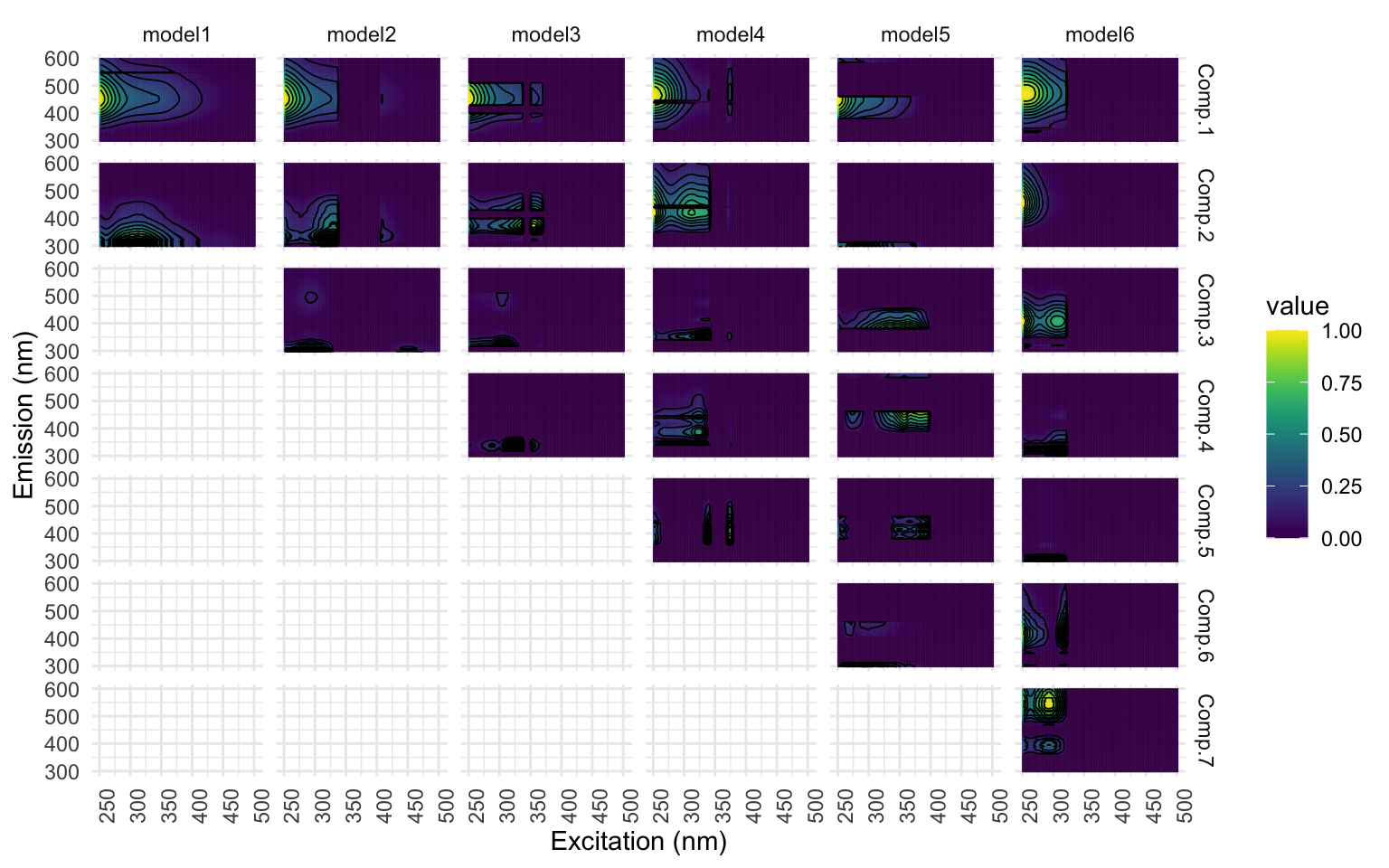
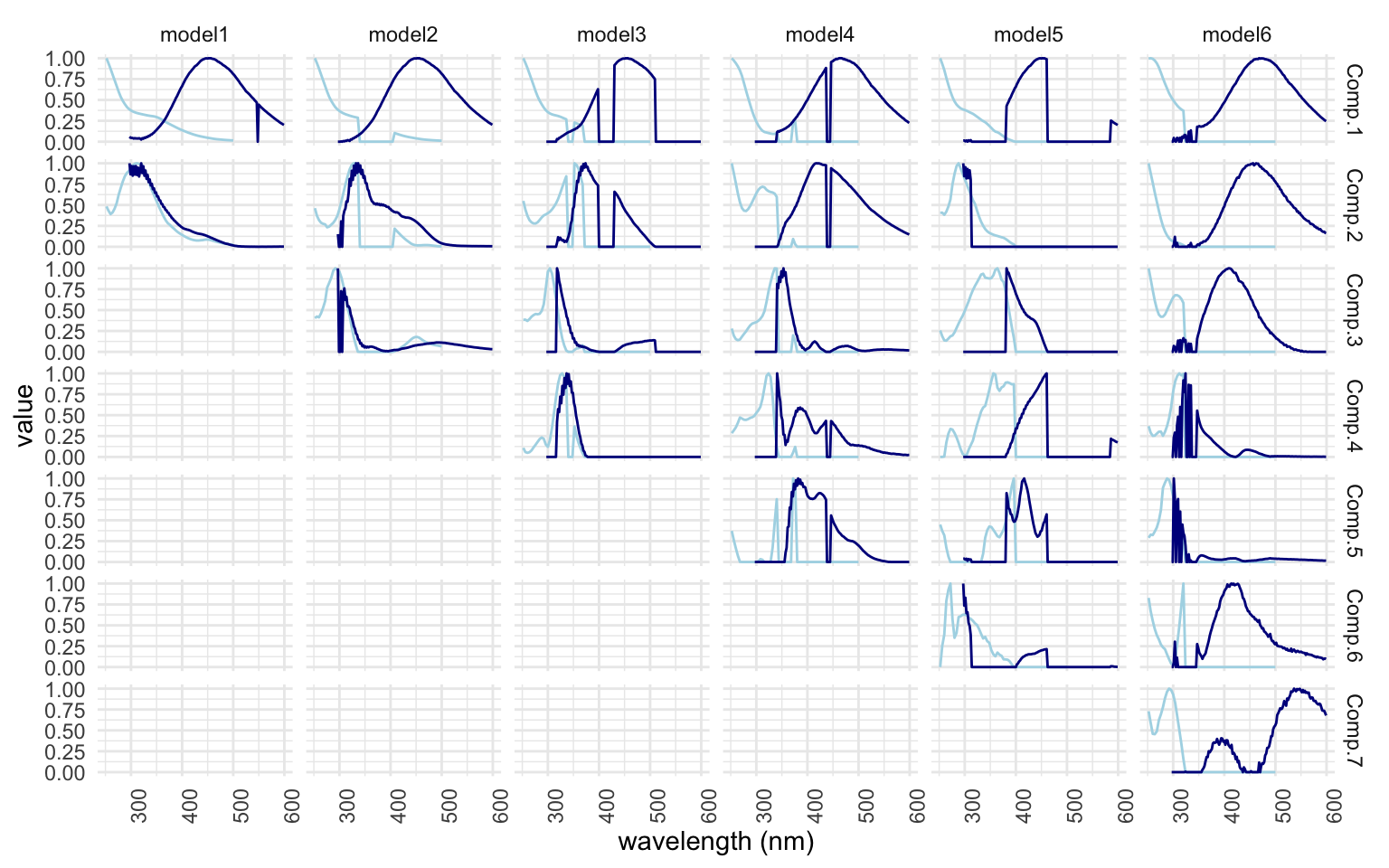
Ici, selon la figure [1] montre le nombre de composantes qui serait idéal, mais notez comment la représentation visuelle de la figure [2] n’est pas belle ; il y a des barres mauve foncé verticales et horizontales qui coupent les ‘hot spots’ des composantes qui se traduisent aussi dans la figure [3]. Les courbes ne sont pas toutes lisses, ce n’est pas beau et tout ça n’est pas souhaitable. * J’ai constaté que le nombre de composantes identifiés comme étant significatif changeait à chaque fois que je roulais le modèle. On va régler cela à l’instant avec l’étape de normalisation.*
Selon Murphy et al., l’algorithme du PARAFAC assume qu’il n’y a pas de corrélation entre les composantes. Dans le cas d’un jeu de données où on a une grande variance dans la quantité de carbone organique dissous (COD / DOC), la corrélation est probable. Ainsi, pour améliorer note modèle préliminaire, on va procéder à la normalisation. On va créer une nouvelle version du modèle (pf2n), redimensionner et afficher les résultats.
pf2n <- eem_parafac(EEMlist, comps = seq(dim_min,dim_max),
normalise = TRUE,
const = c("nonneg", "nonneg", "nonneg"),
maxit = maxit,
nstart = nstart,
ctol = ctol,
cores = cores)
pf2n <- lapply(pf2n, eempf_rescaleBC, newscale = "Fmax")
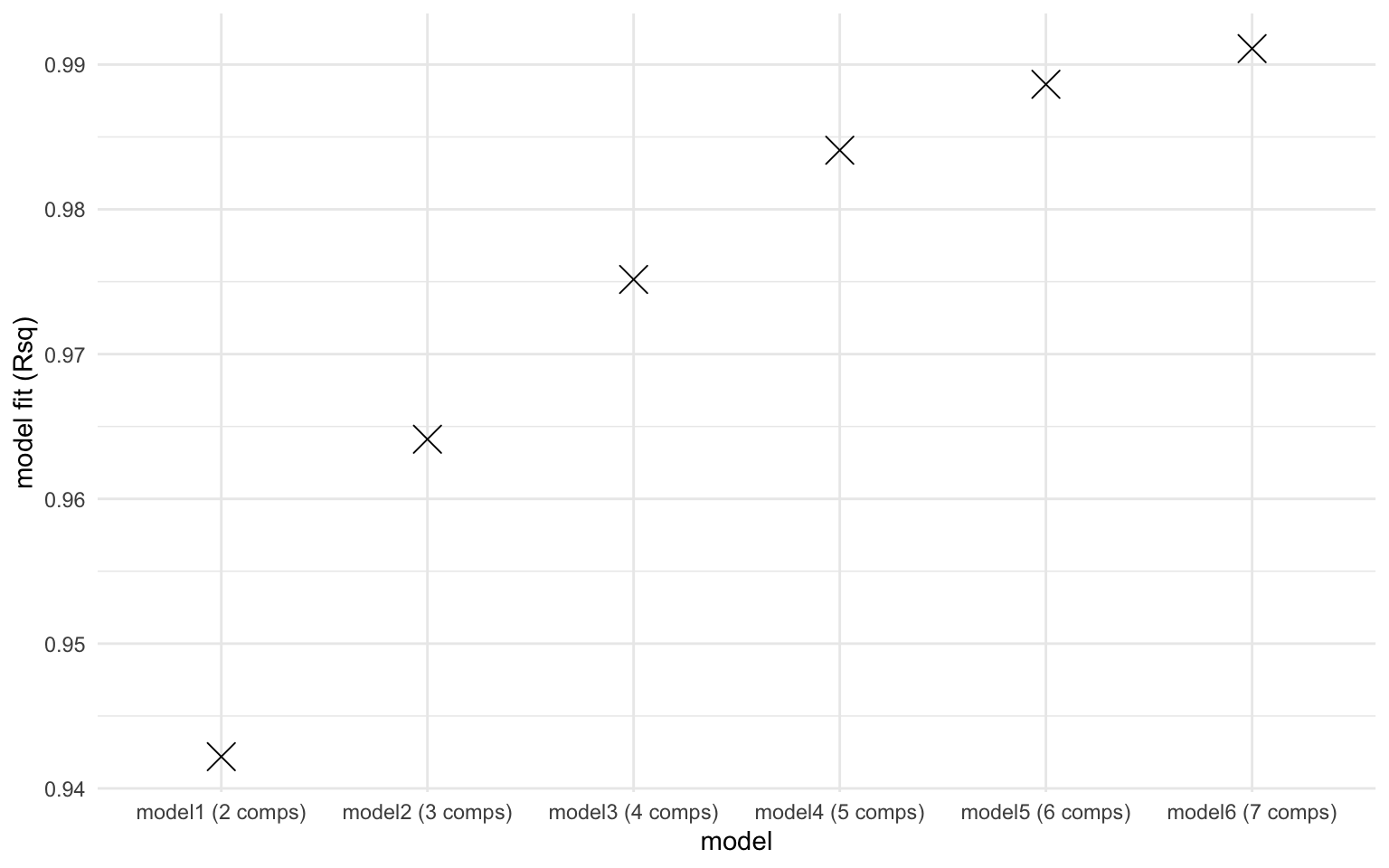
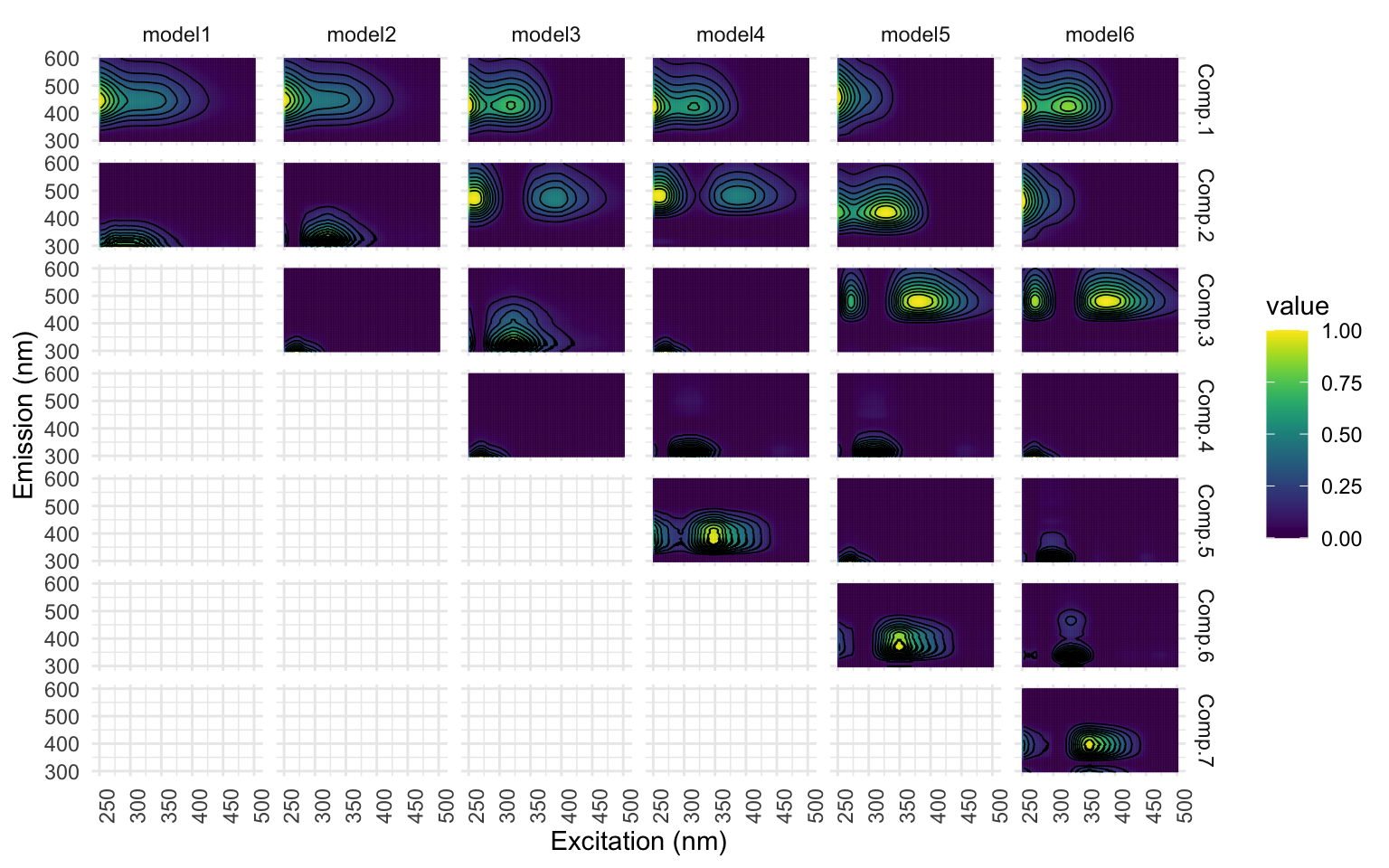
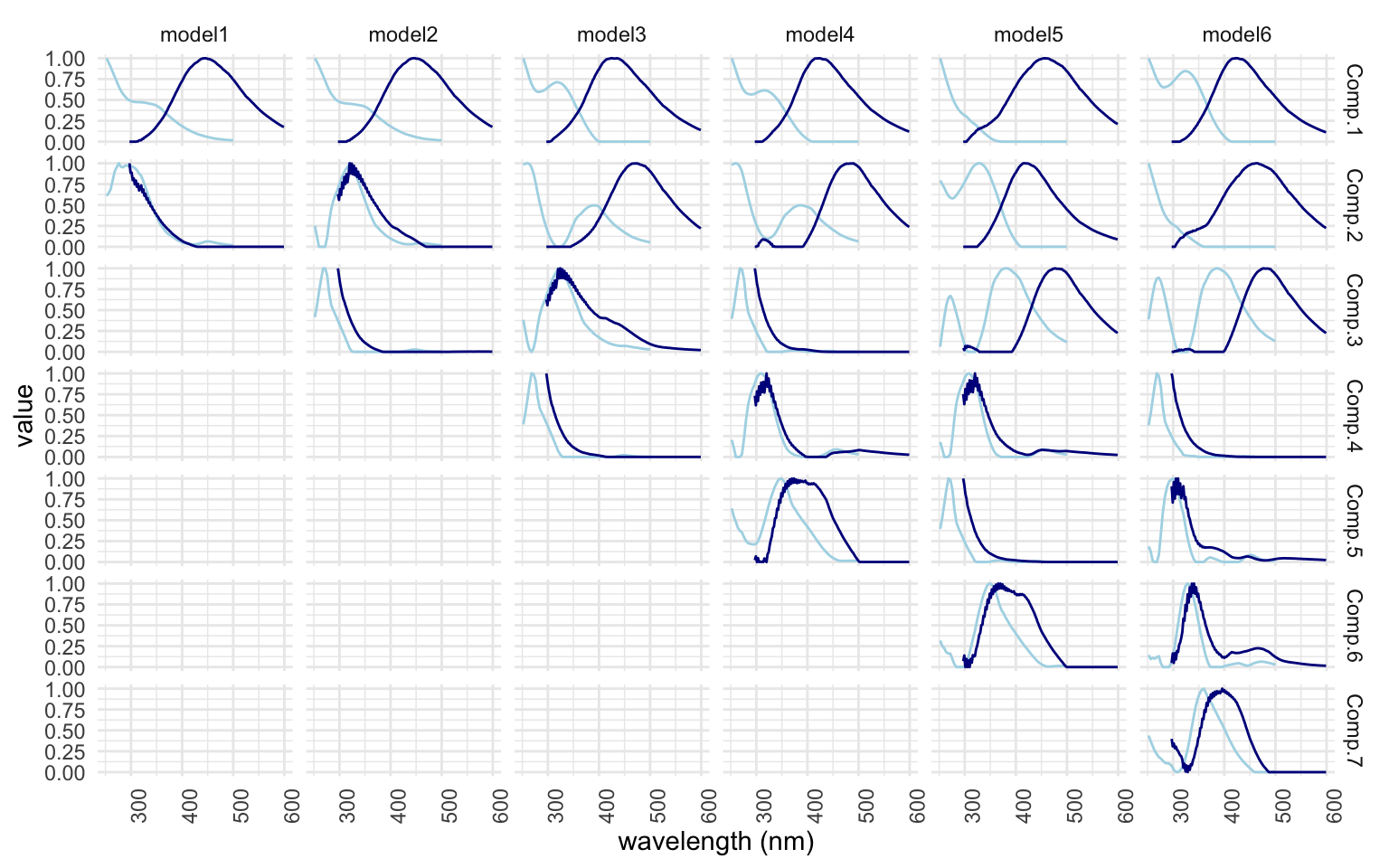
eempf_compare(pf2n, contour = TRUE)
[[1]]
[[2]]
[[3]]
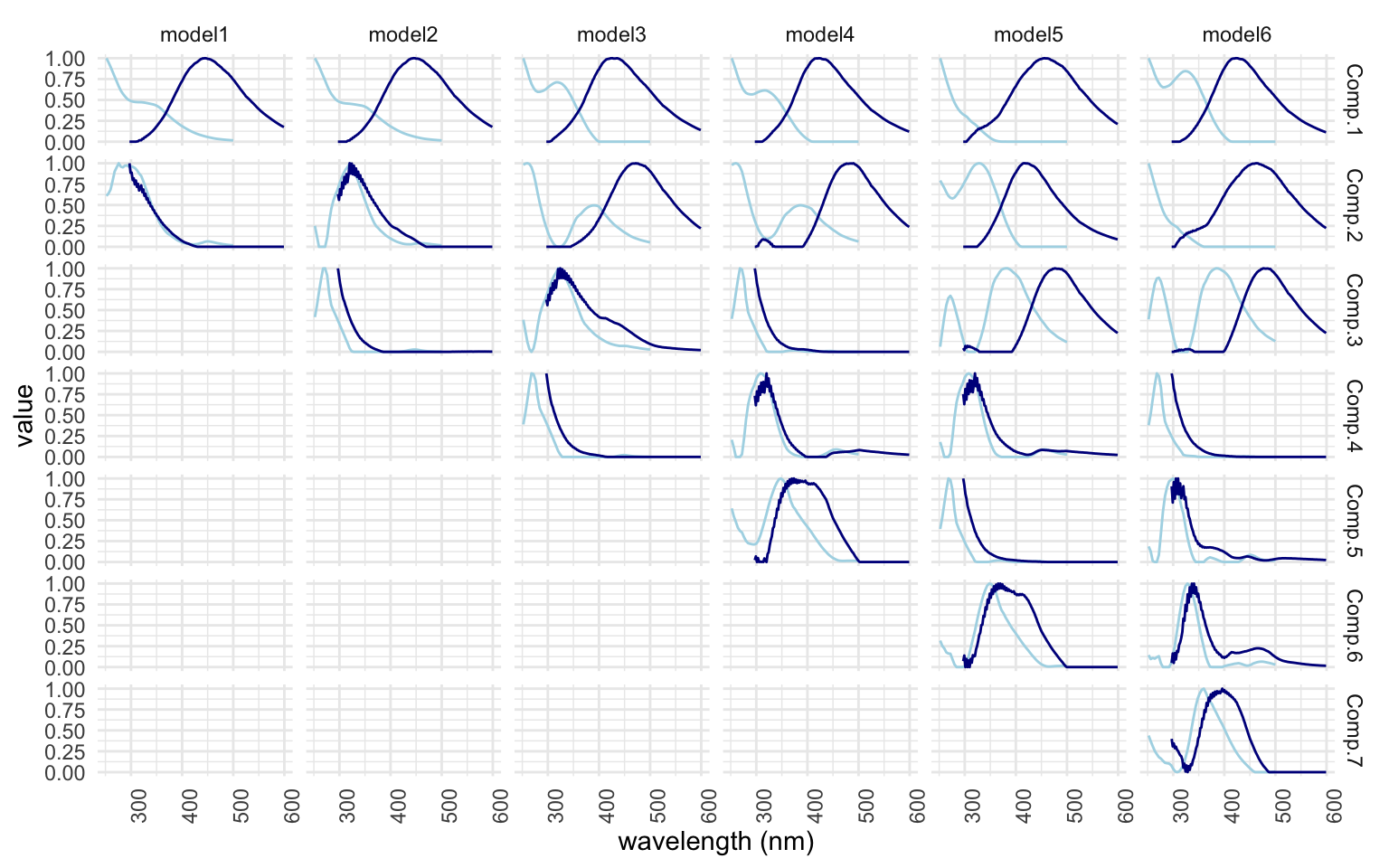
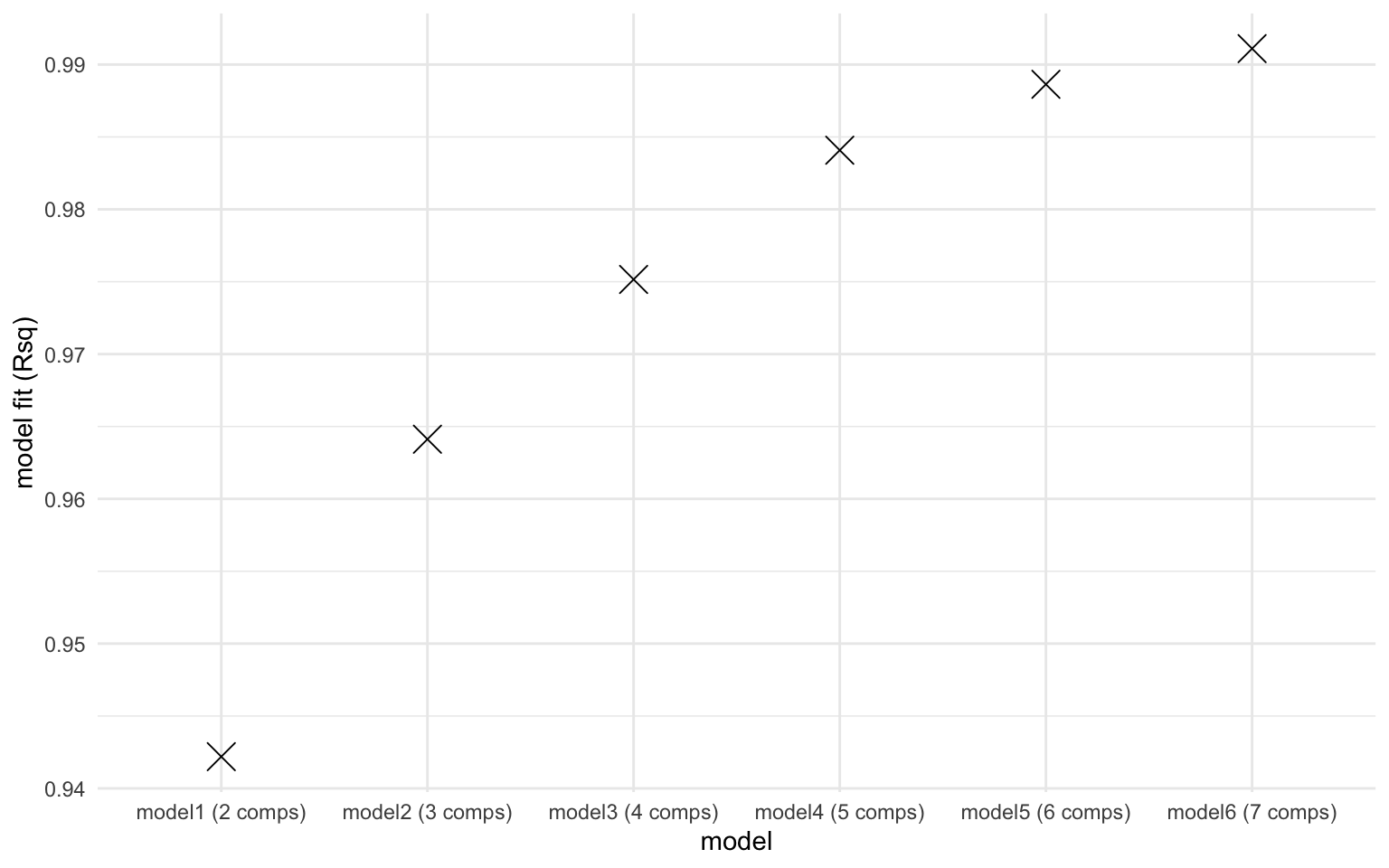
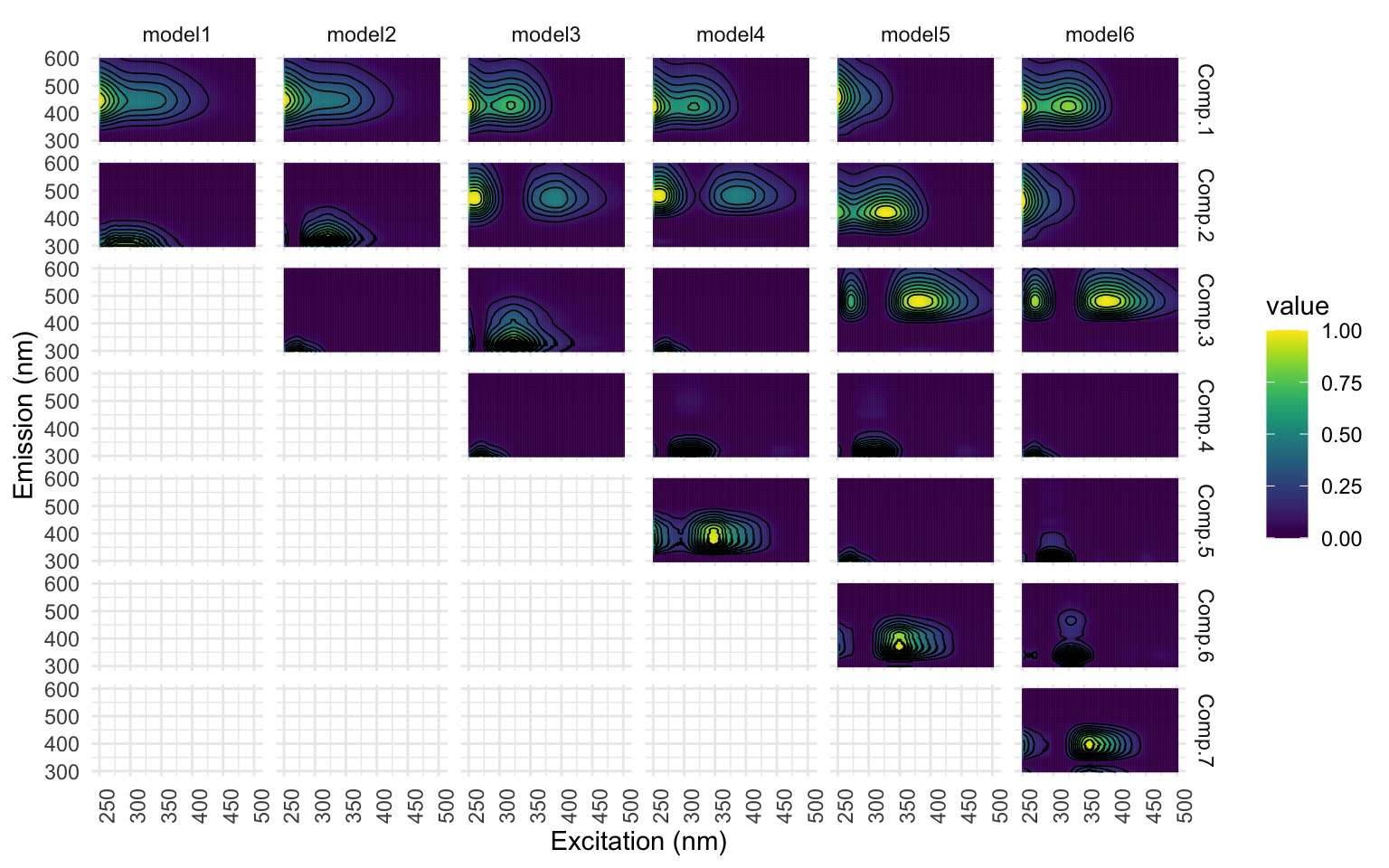
À la lecture des 3 graphiques, le résultat est déjà beaucoup mieux! Dans la fig [1], la signifiance des composantes augmente plus on en as, [2] les cercles colorés ne sont plus coupés et [3] les courbes sont beaucoup plus lisses. Les courbes qui demeurent érratiques montrent des composantes ‘limite’. Nous devrons porter une attention à ces composantes dans les étapes qui suivent: il se peut que nous ne soyons pas en mesure d faire valider un modèle si on choisit de les garder.
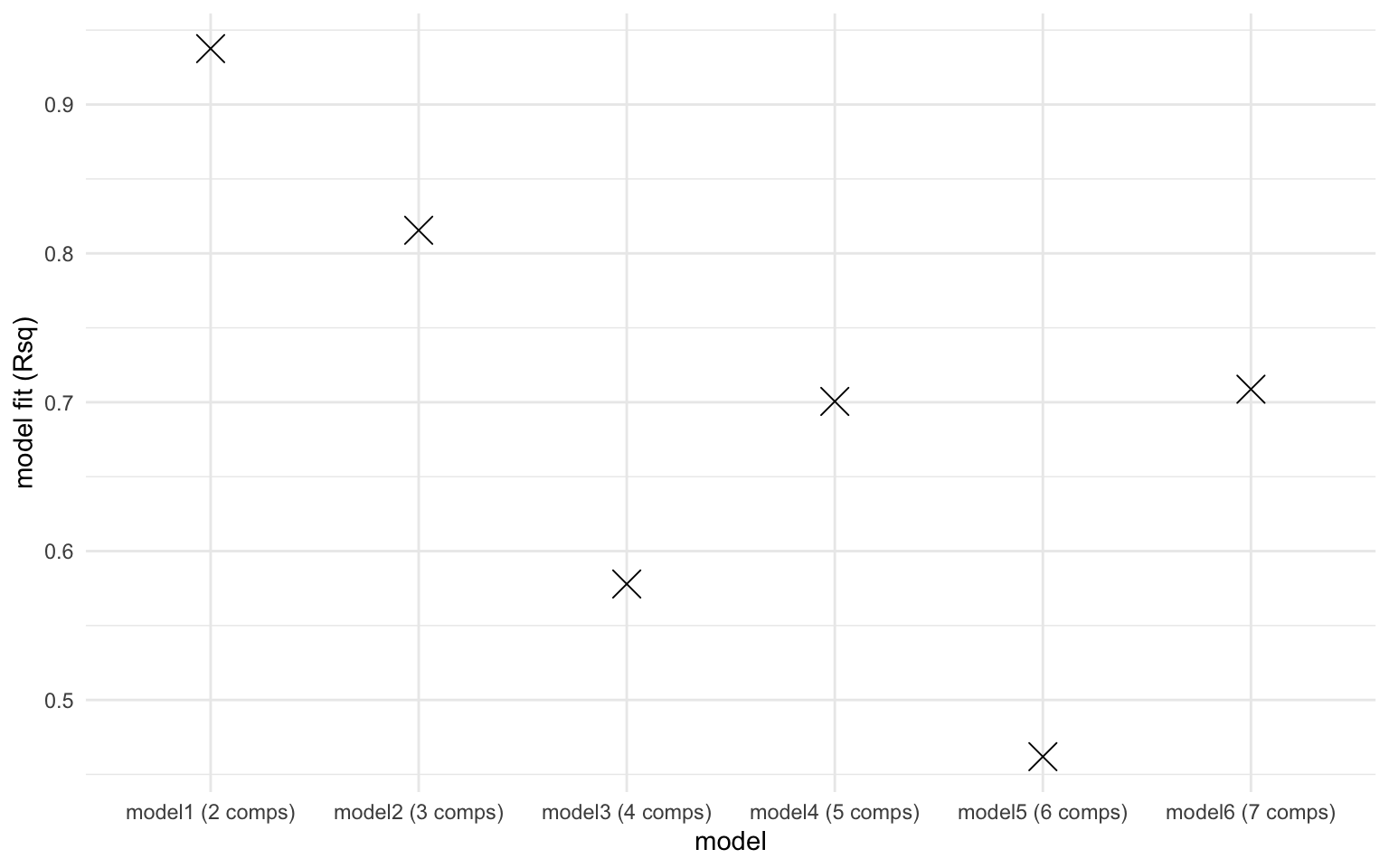
Maintenant, il faut décider du nombre de composantes à garder pour la confection de notre modèle final. ATTENTION Ici, il nous faut indiquer le numéro du modèle et non le nombre de composantes que l’on veut à l’aide de parenthèses carrées [[4]]. Comme on l’a vu dans la sortie ci-dessus, les composantes C4 et C5 du modèle [[4]] sont erratiques. On va essayer de voir si on peut le faire valider. Pour ce faire, on va tenter de nettoyer les signaux en enlevant les échantillons qui peuvent avoir un trop grand levier sur les résultats (des outliers si ont veut).
cpl <- eempf_leverage(pf2n[[4]]) # ici, le chiffre identifie le numéro du modèle, pas le nombre de composantes
eempf_leverage_plot(cpl,qlabel=0.1) # graphique des échantillons leviers (outliers)
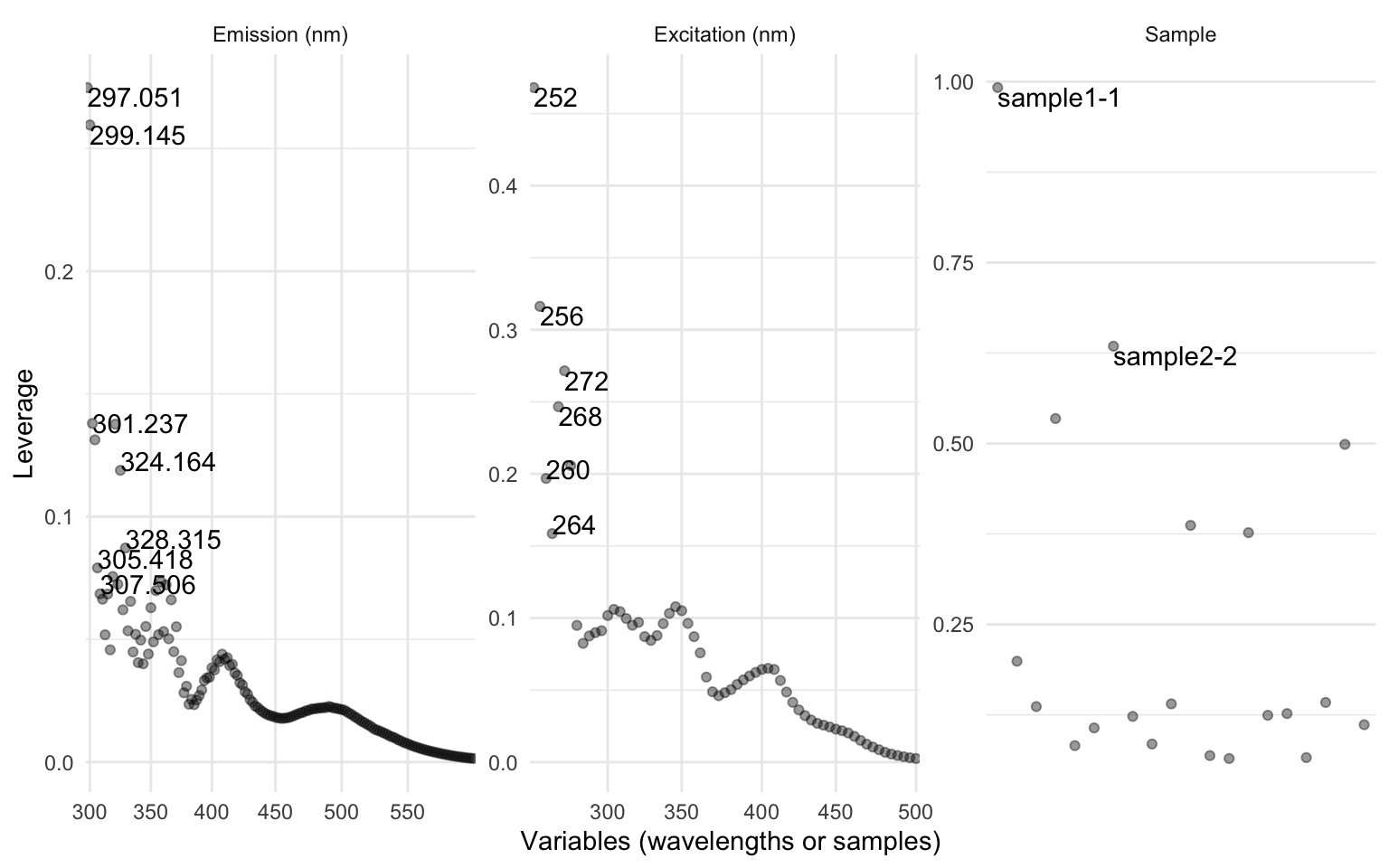
Le graphique à gauche et au centre identifient les longueurs d’ondes (wl) d’excitation et d’émission qui ont un grand effet de levier sur nos composantes. À droite, ce sont les noms des échantillons qui ont un grand effet et que nous allons considérer pour améliorer notre modèle. Dans la vraie vie, vous auriez aussi à faire le même exercice pour les wl. Nous allons manuellement exclure les échantillons problématiques identifiés dans le graphique de droite (“sample1-1” et “sample2-2”) en les fixant dans un objet exclude pour nous permettre de laisser une trace du processus décisionnel itératif. Nous excluons ces échantillons de notre liste d’EEMs originel pour ensuite rouler un nouveau modèle (pf3n) sans ces échantillons leviers. Enfin, il reste à identifier les leviers qui pourraient persister et de recommencer à partir des étapes d’exclusion.
exclude <- list(
"ex" = c(),
"em" = c(),
"sample" = c("sample1-1", "sample2-2")
)
eem_list_ex <- eem_exclude(EEMlist, exclude)
pf3n <- eem_parafac(eem_list_ex, comps = seq(dim_min,dim_max),
normalise = TRUE,
const = c("nonneg", "nonneg", "nonneg"),
maxit = maxit,
nstart = nstart,
ctol = ctol,
cores = cores)
pf3n <- lapply(pf3n, eempf_rescaleBC, newscale = "Fmax")
eempf_leverage_plot(eempf_leverage(pf3n[[4]]),qlabel=0.1)
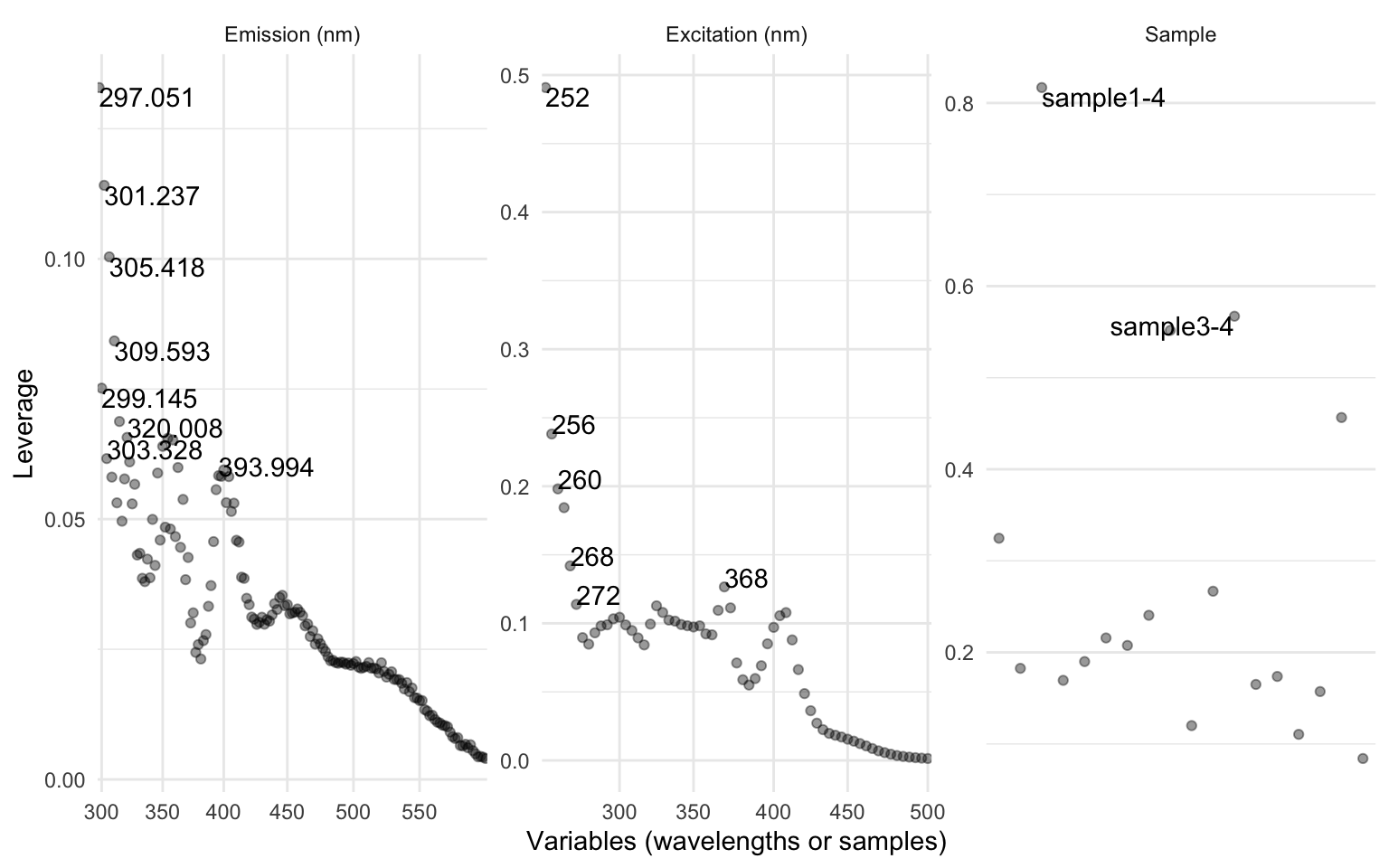
J’ai intentionnellement laissés l’ensemble de ces codes dans le même bloc puisqu’il vous faudra répéter ces étapes jusqu’à ce que vous soyez satisfait d’avoir exclus l’ensemble des échantillons levier. Cette décision est personnelle et dépendra de votre interprétation individuelle. Idéalement, ne pas exclure plus de 10 % de vos échantillons au total pour éviter un modèle trop ajusté (over-fitting). Vous pouvez analyser les résidus pour vous donner un coup de main dans cette décision.
eempf_residuals_plot(pf3n[[4]], EEMlist, residuals_only = TRUE, spp = 9, cores = cores, contour = TRUE)
[[1]]
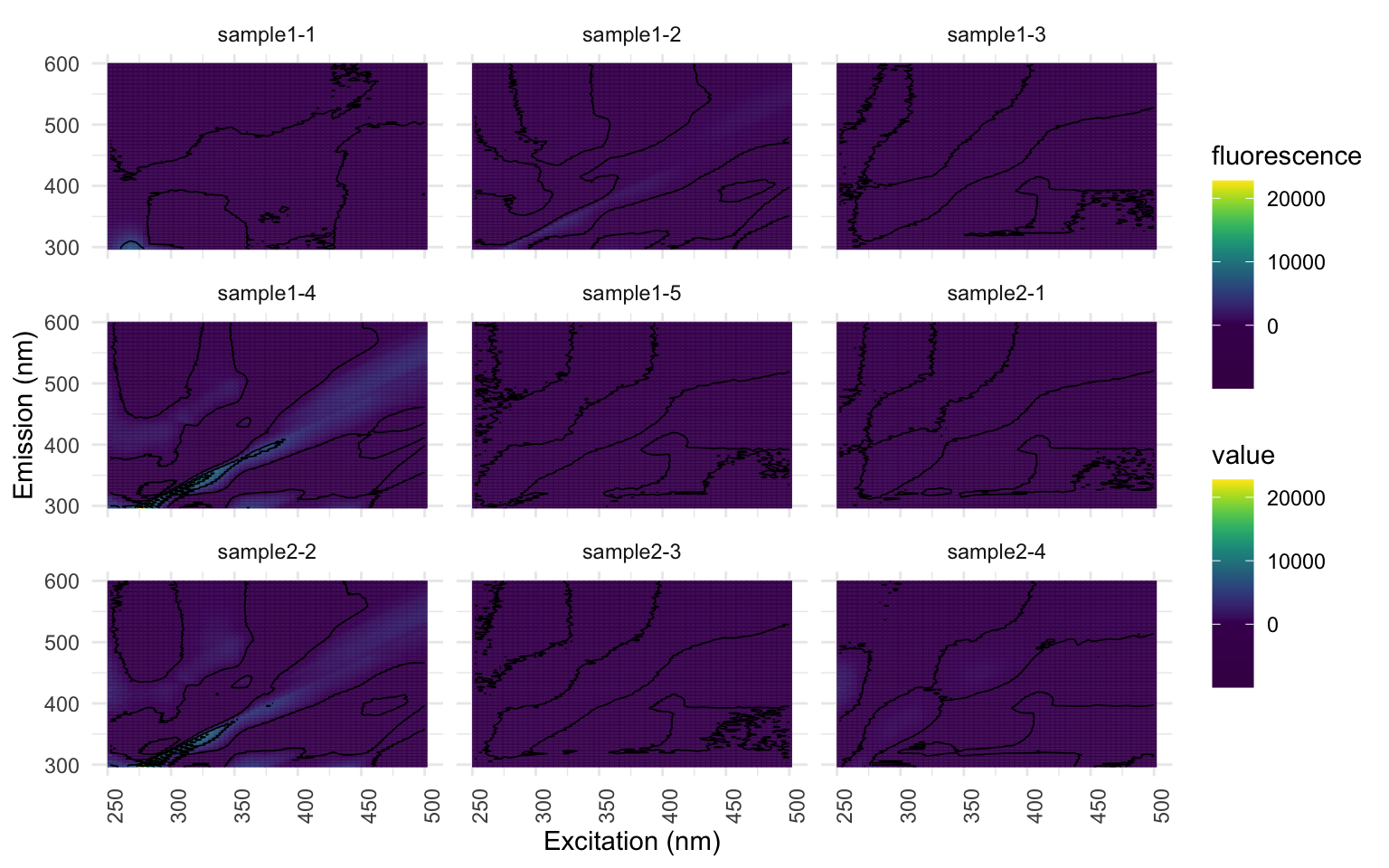
[[2]]
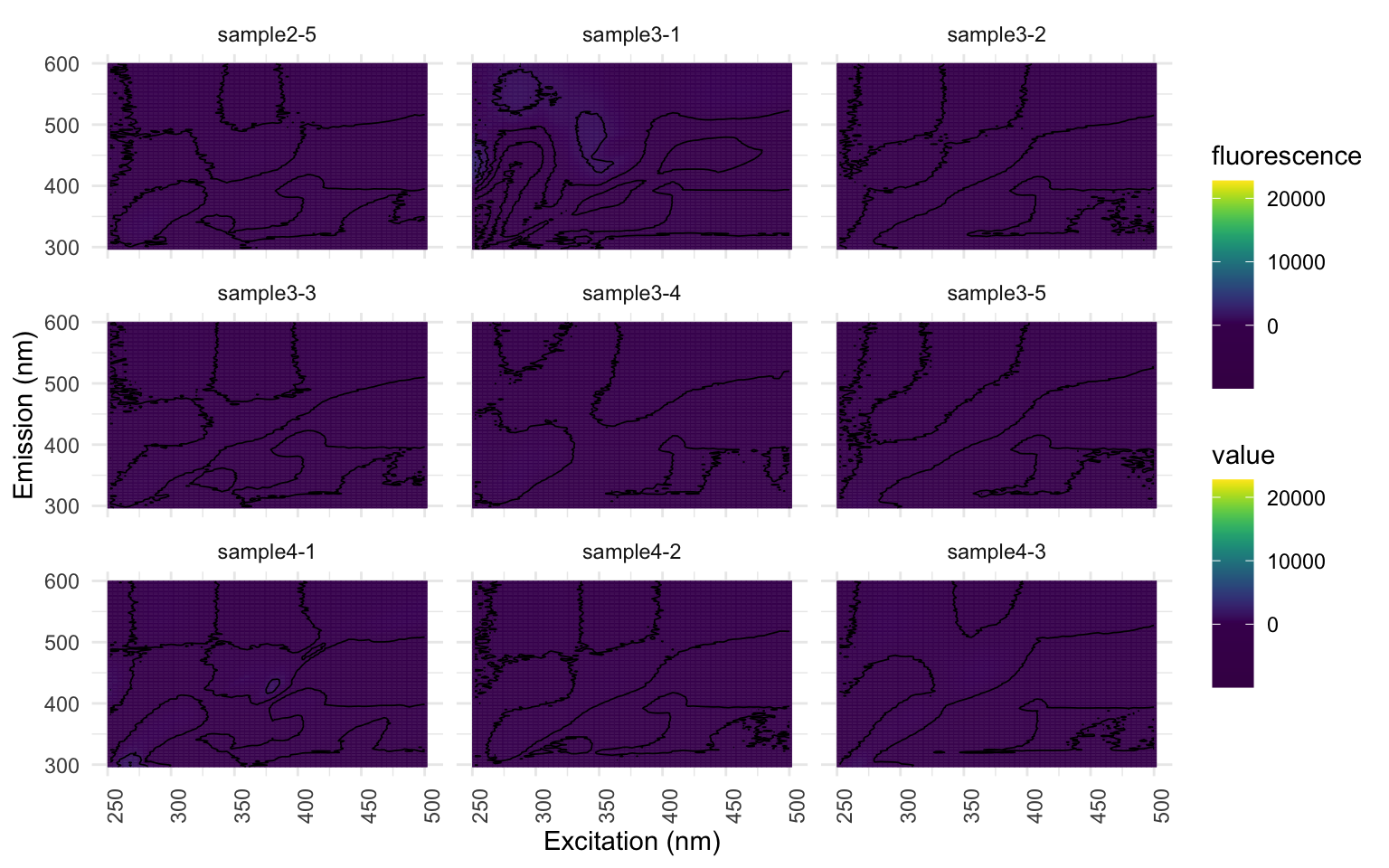
[[3]]
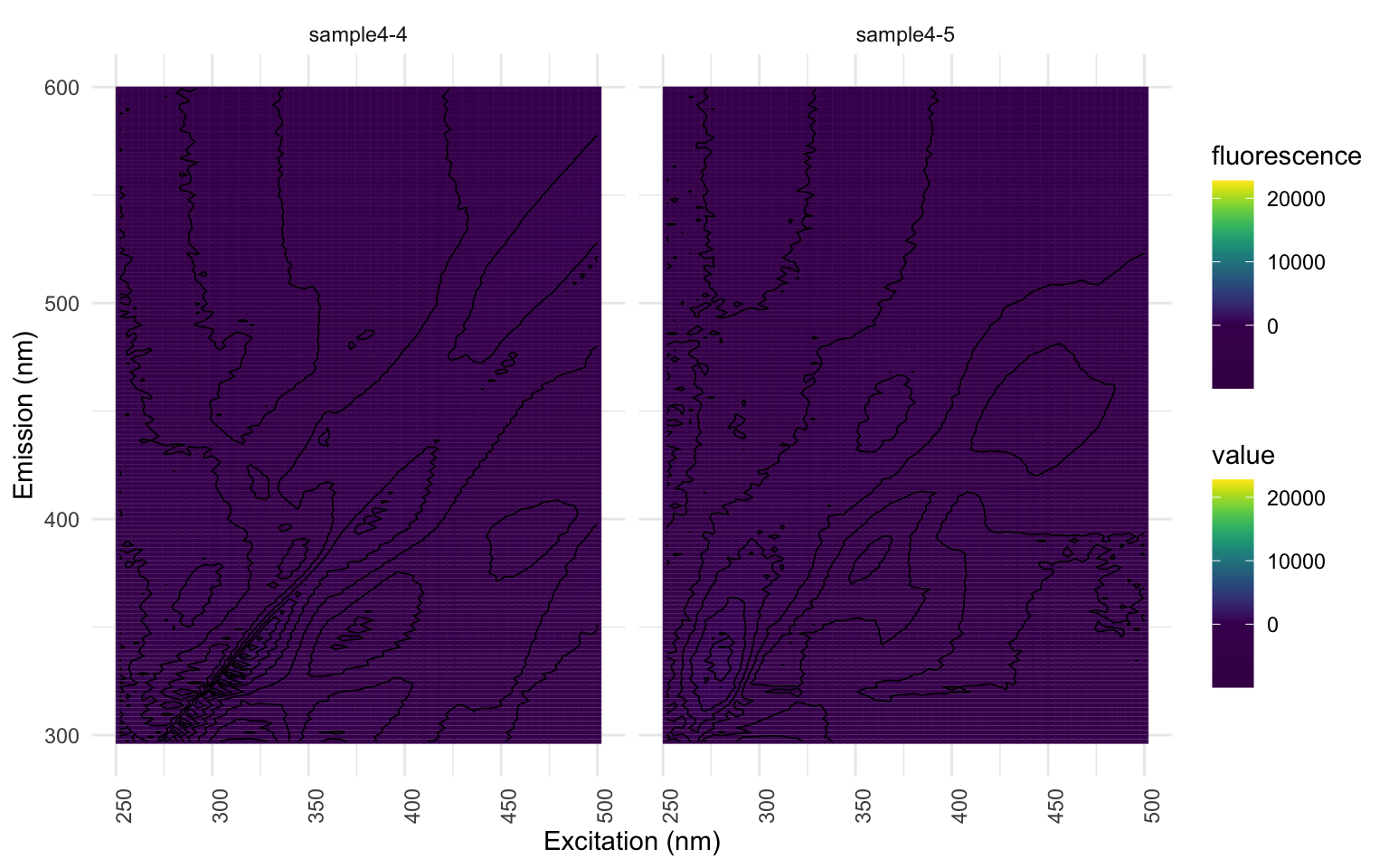
Voyez comment les seules hot-spots qui demeurent sont les bandes des échantillons “sample1-2”, “sample1-4”, “sample2-2” et “sample4-4”? Ces échantillons ont donc un effet levier sur le modèle.
Donc! Maintenant que nous sommes finalement satisfaits de notre modèle préliminaire à la suite de toutes ces étapes de perfectionnement, précédons à créer notre modèle final.
Modèle final
Pour finaliser notre modèle, on va d’abord réduire le seuil de tolérance du paramètre ctol et augmenter le nombre d’itérations maxit. On va aussi spécifier dans la fonction le nombre de composantes qu’on veut garder avec l’argument comps = 5. ATTENTION Ici il s’agit vraiment du nombre de composante et non du numéro de modèle.
ctol <- 10^-8 # réduit le seuil de tolérance
nstart = 20
maxit = 10000 # augmente le nombre maximal d'itérations
pf4 <- eem_parafac(eem_list_ex,
comps = 5, # inscrire le nombre de composantes ici
normalise = TRUE,
const = c("nonneg", "nonneg", "nonneg"),
maxit = maxit,
nstart = nstart,
ctol = ctol,
output = "all",
cores = cores,
strictly_converging = TRUE)
pf4 <- lapply(pf4, eempf_rescaleBC, newscale = "Fmax")
eempf_convergence(pf4[[1]]) # valider que le modèle converge.
Calculated models: 20
Converging models: 20
Not converging Models, iteration limit reached: 0
Not converging models, other reasons: 0
Best SSE: 3266.651
Summary of SSEs of converging models:
Min. 1st Qu. Median Mean 3rd Qu. Max.
3267 3267 3385 4130 3388 18325
La sortie de la fonction eempf_converge permet de nous assurer que le modèle a bel et bien convergé.
On peut afficher la représentation visuelle des composantes [1] et de leur loadings [2]…
eempf_comp_load_plot(pf4[[1]], contour = TRUE) # graphique 1) représentation visuelle des composantes et 2) apport des composantes dans chaque échantillon (loadings)
[[1]]
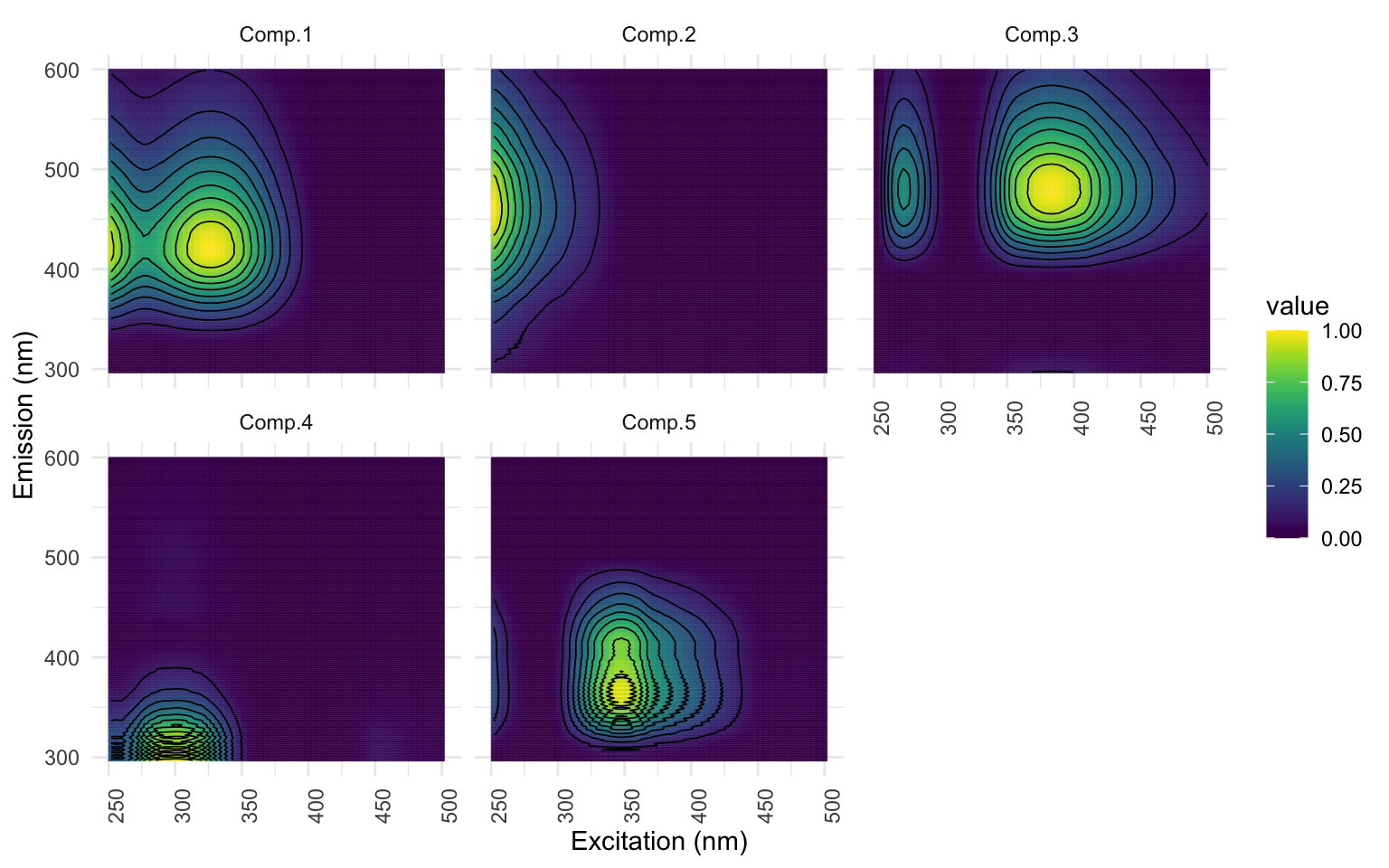
[[2]]
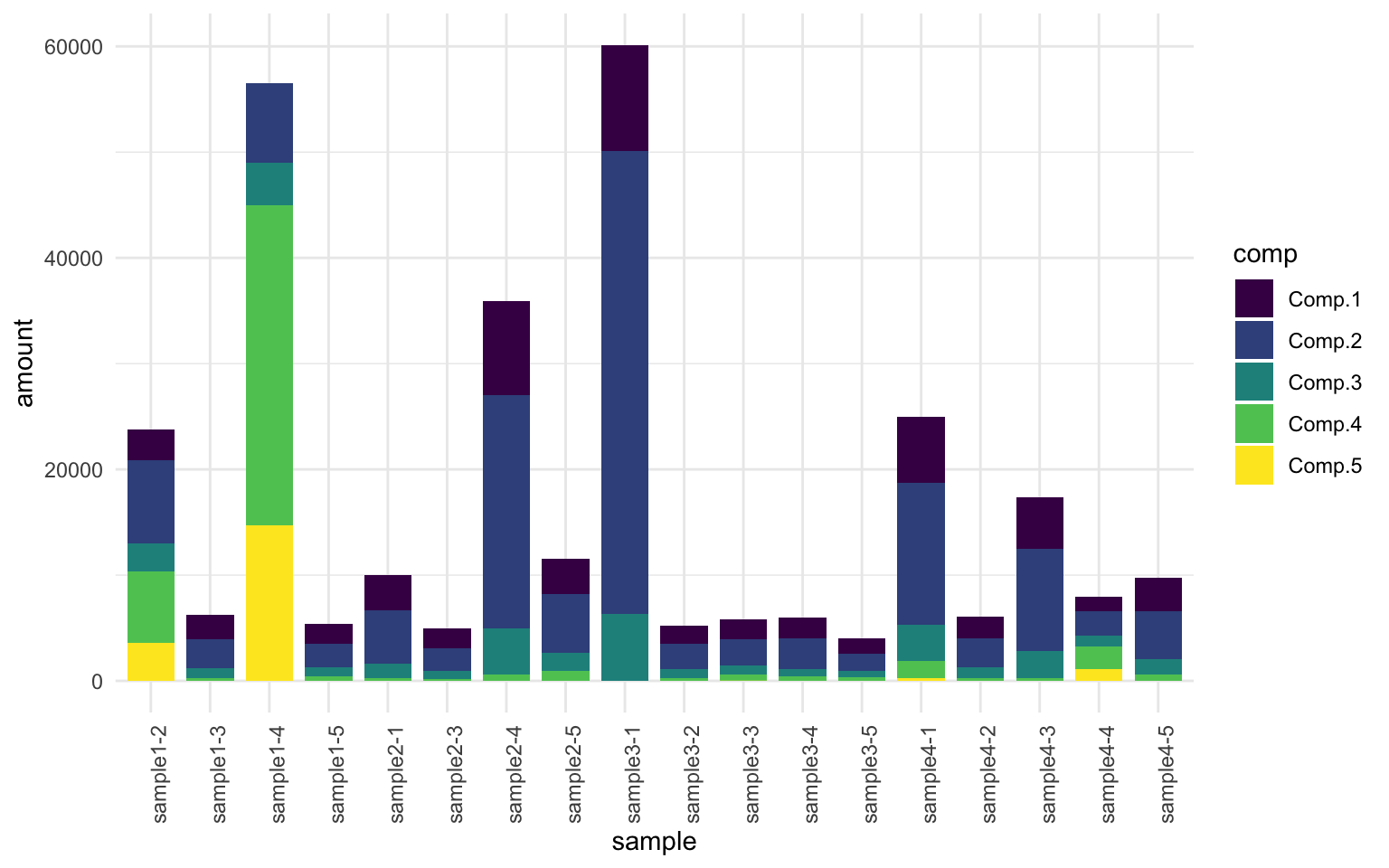
… et aussi changer le nom des composantes pour enjoliver notre graphique :
eempf_comp_names(pf4) <- c("C1","Peak A","C3","Proteic-like","Mr. Kibbles") # insérer autant de noms que vous avez de composantes
pf4[[1]] %>%
ggeem(contour = TRUE)
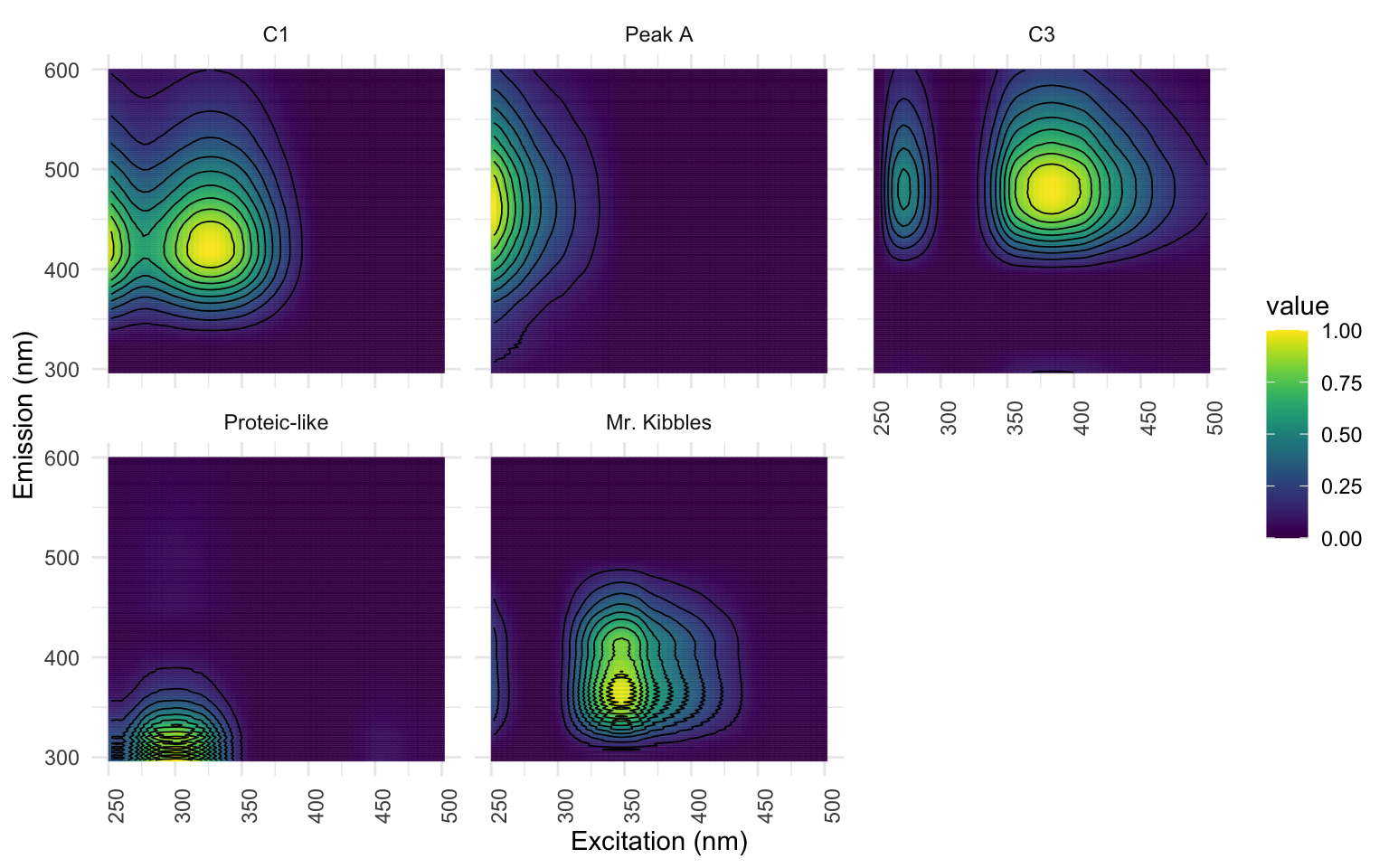
Ensuite, il est essentiel de procéder à l’étape de validation par split-half analysis. Cette méthode est bien détaillée dans l’article de Murphy et al. (2013). En somme, la sortie montre l’intensité des EEMs vue de côté pour chaque sous-groupe créé lors de l’analyse. Pour chaque composante, nous devrions voir la convergeance parfaite de chacune de ces lignes. Les lignes pointillées identifient un PEAK secondaire et devrait aussi converger pour chaque sous-groupe.
sh <- splithalf(eem_list_ex, 5, normalise = TRUE, rand = FALSE, cores = cores, nstart = nstart, strictly_converging = TRUE, maxit = maxit, ctol = ctol) # l'analyse en sois
splithalf_plot(sh) # le graphique du split half analysis
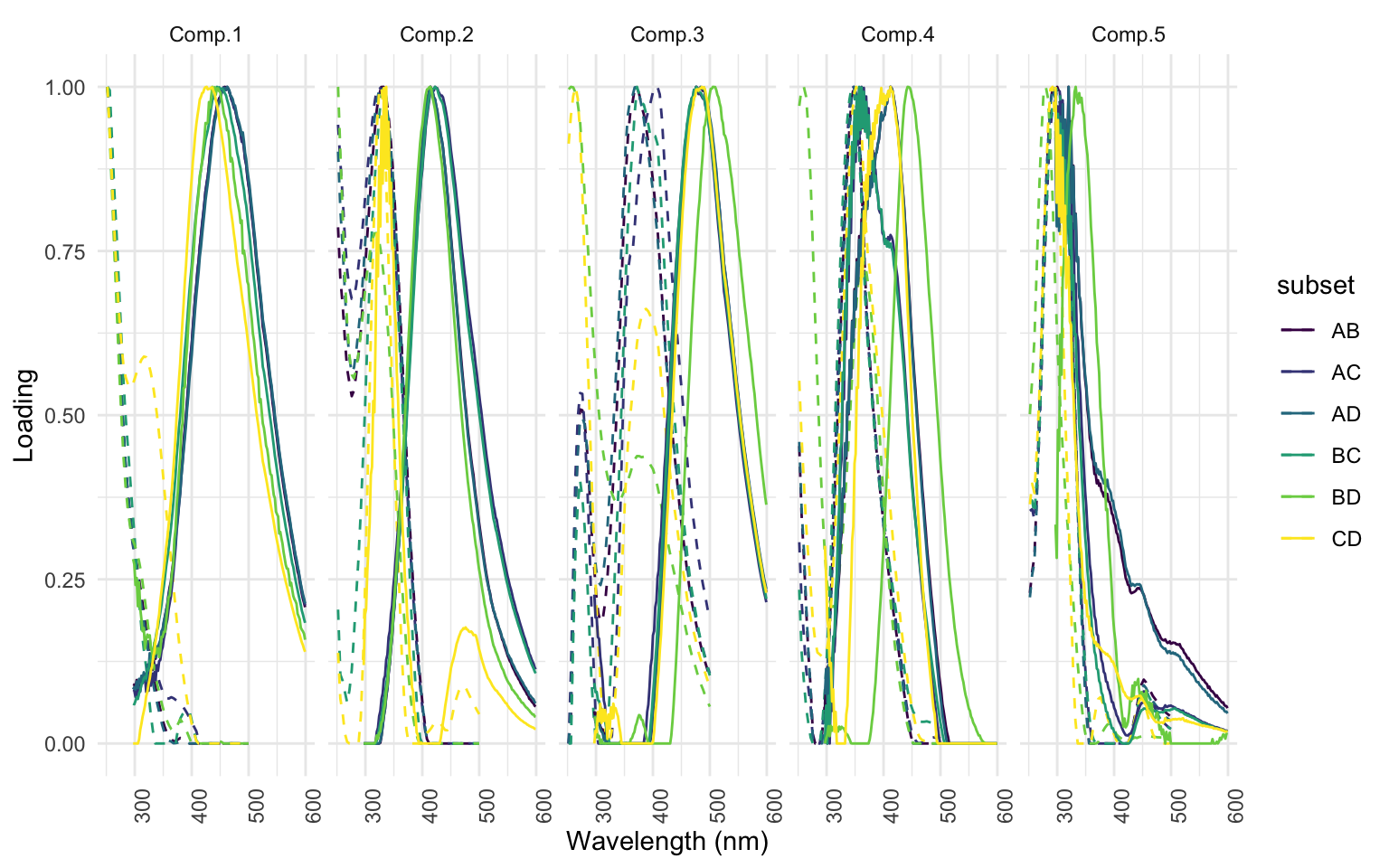
On peut aussi voir la correspondance de chacun des sous-groupes par l’affichage de l’objet tcc_sh_table.
tcc_sh_table <- splithalf_tcc(sh) # validation numérique de la similarité entre les pairs de données dans l'analyse
tcc_sh_table
component comb tcc_em tcc_ex
1 Comp.1 ABvsCD 0.8755677 0.3181844
2 Comp.1 ACvsBD 0.9968291 0.9867063
3 Comp.1 ADvsBC 0.9946090 0.9936358
4 Comp.2 ABvsCD 0.8249520 0.9727518
5 Comp.2 ACvsBD 0.9802167 0.8916440
6 Comp.2 ADvsBC 0.9174102 0.9886498
7 Comp.3 ABvsCD 0.8249549 0.9986905
8 Comp.3 ACvsBD 0.8810485 0.8475137
9 Comp.3 ADvsBC 0.9656290 0.9990002
10 Comp.4 ABvsCD 0.9818775 0.9691543
11 Comp.4 ACvsBD 0.6818575 0.8836056
12 Comp.4 ADvsBC 0.9880365 0.9647530
13 Comp.5 ABvsCD 0.9341904 0.9247569
14 Comp.5 ACvsBD 0.7242248 0.8190361
15 Comp.5 ADvsBC 0.9975157 0.8992815
Exporter le modèle et les résultats de nos données
Il existe une base de données open source où les gens téléversent leur modèle : Open Fluor. À l’aide d’Open Fluor, il est possible de charger notre modèle et de le comparer à ceux déjà publiés afin de nous aider dans l’identification de nos composantes et donc à l’interprétation de nos résultats. Si vous souhaitez publier votre modèle pour que les autres puissent en bénéficier, n’oubliez pas re remplir manuellement les champs en haut de page pour identifier votre travail et la nature de vos échantillons.
eempf_openfluor(pf4[[1]], file = "1.OpenFluor_Model.txt")
Je vous recommande fortement d’extraire les coordonnées de vos composantes en parallèle à votre travail d’identification et d’interprétation de vos composantes. C’est un peu de pénible, mais en gros, il faut chercher le wavelength ou il y a un 1.00000 dans les tableaux ex et em. Je tiens à remercier Jade pour son aide pour cette étape!
em <- data.frame(pf4[[1]][["B"]]) # "B" is for Emission
ex <- data.frame(pf4[[1]][["C"]]) # "C" is for Excitation
Ainsi, vous allez pourvoir comparer les PEAKs de vos composantes avec celles identifiées par Open Fluor afin d’éviter des erreurs (J’ai moi même évité des erreurs en réalisant cette double validation…). Dans notre exemple, voici ls coordonnées que vous devriez avoir pour les 5 composantes:
- C1 : 328 , 422
- C2 : 252 , 462
- C3 : 384 , 476
- C4 : 300 , 297
- C5 : 348 , 365
StaRdom permet aussi de produire une page HTLM qui affiche toutes les décisions que vous avez prise pour produire votre modèle et les résultats découlant. À garder dans vos archives à quelque part ;)
eempf_report(pf4[[1]], export = "2.Parafac_Report.html", eem_list = eem_list_ex, shmodel = sh, performance = TRUE)
Finalement, nous pouvons procéder à l’exportation de nos résultats : soit la composition des échantillons, ou la quantité de chaque composante que l’on retrouve dans chacun de nos échantillons. Sachez que la fonction s’applique ici uniquement aux échantillons inclus dans le modèle. Jade m’informe qu’elle travaillera avec Matthias Pucher pour perfectionner cette fonction afin d’exporter les données pour l’ensemble de vos échantillons… à suivre!
model<- eempf_export(pf4[[1]], export = NULL, Fmax = TRUE)
write.csv(model, "3.Results.csv")
Traditionnellement, on compare le pourcentage et non la valeur r.u. (raman units). Pour obtenir les pourcentages, c’est aussi simple que de créer une colonne qui additionne l’ensemble des composantes pour une ligne et de faire une règle de 3 pour obtenir le pourcentage des composantes pour chaque échantillon.
Félicitations! Vous êtes arrivés au bout!