Introduction au Machine learning et à la classification dans R
Arthur de Grandpré
Juin 2024
- Pourquoi le Machine learning?
- Exemple #1 : Prédire une espèce à partir de traits
- Classification non supervisée
- Classification Supervisée
- Arbres décisionnels (Decision Trees)
- Méthodes d’ensembles
- Exemple #2
- GOI: Gradient information Optimization
- Gradient Forests
Pourquoi le Machine learning?
-
Pour exploiter un grand nombre de variables indépendantes afin d’éffectuer des prédictions.
-
Pour extraire les variables indépendantes les plus importantes d’un ensemble pour expliquer un effet.
-
Pour déterminer quelles sont les variables à prioriser dans un ensemble.
-
Utile pour de nombreuses applications :
-
Reconnaissance d’images (Identification d’espèces via mesures morphométriques, ex. zooplancton)
-
Télédétection (Identification de classes d’utilisation du territoire)
-
Modélisation multivariée
-
Exemple #1 : Prédire une espèce à partir de traits
En utilisant la base de données Iris, est-il possible de prédire les espèces de fleur à partir des traits mesurés?
#install.packages("nom_du_package") # pour installer un package
library(tidyverse)
── Attaching core tidyverse packages ──────────────────────── tidyverse 2.0.0 ──
✔ dplyr 1.1.4 ✔ readr 2.1.5
✔ forcats 1.0.0 ✔ stringr 1.5.1
✔ ggplot2 3.5.1 ✔ tibble 3.2.1
✔ lubridate 1.9.3 ✔ tidyr 1.3.1
✔ purrr 1.0.2
── Conflicts ────────────────────────────────────────── tidyverse_conflicts() ──
✖ dplyr::filter() masks stats::filter()
✖ dplyr::lag() masks stats::lag()
ℹ Use the conflicted package (<http://conflicted.r-lib.org/>) to force all conflicts to become errors
library(randomForest)
randomForest 4.7-1.1
Type rfNews() to see new features/changes/bug fixes.
Attaching package: 'randomForest'
The following object is masked from 'package:dplyr':
combine
The following object is masked from 'package:ggplot2':
margin
library(class)
library(ranger)
Attaching package: 'ranger'
The following object is masked from 'package:randomForest':
importance
library(vegan)
Loading required package: permute
Loading required package: lattice
This is vegan 2.6-6.1
library(FactoMineR)
library(factoextra)
Welcome! Want to learn more? See two factoextra-related books at https://goo.gl/ve3WBa
library(ggpubr)
library(caret)
Attaching package: 'caret'
The following object is masked from 'package:vegan':
tolerance
The following object is masked from 'package:purrr':
lift
Pour commencer, explorons la base de données iris, comprise dans R.
data("iris")
iris
Sepal.Length Sepal.Width Petal.Length Petal.Width Species
1 5.1 3.5 1.4 0.2 setosa
2 4.9 3.0 1.4 0.2 setosa
3 4.7 3.2 1.3 0.2 setosa
4 4.6 3.1 1.5 0.2 setosa
5 5.0 3.6 1.4 0.2 setosa
6 5.4 3.9 1.7 0.4 setosa
7 4.6 3.4 1.4 0.3 setosa
8 5.0 3.4 1.5 0.2 setosa
9 4.4 2.9 1.4 0.2 setosa
10 4.9 3.1 1.5 0.1 setosa
11 5.4 3.7 1.5 0.2 setosa
12 4.8 3.4 1.6 0.2 setosa
13 4.8 3.0 1.4 0.1 setosa
14 4.3 3.0 1.1 0.1 setosa
15 5.8 4.0 1.2 0.2 setosa
16 5.7 4.4 1.5 0.4 setosa
17 5.4 3.9 1.3 0.4 setosa
18 5.1 3.5 1.4 0.3 setosa
19 5.7 3.8 1.7 0.3 setosa
20 5.1 3.8 1.5 0.3 setosa
21 5.4 3.4 1.7 0.2 setosa
22 5.1 3.7 1.5 0.4 setosa
23 4.6 3.6 1.0 0.2 setosa
24 5.1 3.3 1.7 0.5 setosa
25 4.8 3.4 1.9 0.2 setosa
26 5.0 3.0 1.6 0.2 setosa
27 5.0 3.4 1.6 0.4 setosa
28 5.2 3.5 1.5 0.2 setosa
29 5.2 3.4 1.4 0.2 setosa
30 4.7 3.2 1.6 0.2 setosa
31 4.8 3.1 1.6 0.2 setosa
32 5.4 3.4 1.5 0.4 setosa
33 5.2 4.1 1.5 0.1 setosa
34 5.5 4.2 1.4 0.2 setosa
35 4.9 3.1 1.5 0.2 setosa
36 5.0 3.2 1.2 0.2 setosa
37 5.5 3.5 1.3 0.2 setosa
38 4.9 3.6 1.4 0.1 setosa
39 4.4 3.0 1.3 0.2 setosa
40 5.1 3.4 1.5 0.2 setosa
41 5.0 3.5 1.3 0.3 setosa
42 4.5 2.3 1.3 0.3 setosa
43 4.4 3.2 1.3 0.2 setosa
44 5.0 3.5 1.6 0.6 setosa
45 5.1 3.8 1.9 0.4 setosa
46 4.8 3.0 1.4 0.3 setosa
47 5.1 3.8 1.6 0.2 setosa
48 4.6 3.2 1.4 0.2 setosa
49 5.3 3.7 1.5 0.2 setosa
50 5.0 3.3 1.4 0.2 setosa
51 7.0 3.2 4.7 1.4 versicolor
52 6.4 3.2 4.5 1.5 versicolor
53 6.9 3.1 4.9 1.5 versicolor
54 5.5 2.3 4.0 1.3 versicolor
55 6.5 2.8 4.6 1.5 versicolor
56 5.7 2.8 4.5 1.3 versicolor
57 6.3 3.3 4.7 1.6 versicolor
58 4.9 2.4 3.3 1.0 versicolor
59 6.6 2.9 4.6 1.3 versicolor
60 5.2 2.7 3.9 1.4 versicolor
61 5.0 2.0 3.5 1.0 versicolor
62 5.9 3.0 4.2 1.5 versicolor
63 6.0 2.2 4.0 1.0 versicolor
64 6.1 2.9 4.7 1.4 versicolor
65 5.6 2.9 3.6 1.3 versicolor
66 6.7 3.1 4.4 1.4 versicolor
67 5.6 3.0 4.5 1.5 versicolor
68 5.8 2.7 4.1 1.0 versicolor
69 6.2 2.2 4.5 1.5 versicolor
70 5.6 2.5 3.9 1.1 versicolor
71 5.9 3.2 4.8 1.8 versicolor
72 6.1 2.8 4.0 1.3 versicolor
73 6.3 2.5 4.9 1.5 versicolor
74 6.1 2.8 4.7 1.2 versicolor
75 6.4 2.9 4.3 1.3 versicolor
76 6.6 3.0 4.4 1.4 versicolor
77 6.8 2.8 4.8 1.4 versicolor
78 6.7 3.0 5.0 1.7 versicolor
79 6.0 2.9 4.5 1.5 versicolor
80 5.7 2.6 3.5 1.0 versicolor
81 5.5 2.4 3.8 1.1 versicolor
82 5.5 2.4 3.7 1.0 versicolor
83 5.8 2.7 3.9 1.2 versicolor
84 6.0 2.7 5.1 1.6 versicolor
85 5.4 3.0 4.5 1.5 versicolor
86 6.0 3.4 4.5 1.6 versicolor
87 6.7 3.1 4.7 1.5 versicolor
88 6.3 2.3 4.4 1.3 versicolor
89 5.6 3.0 4.1 1.3 versicolor
90 5.5 2.5 4.0 1.3 versicolor
91 5.5 2.6 4.4 1.2 versicolor
92 6.1 3.0 4.6 1.4 versicolor
93 5.8 2.6 4.0 1.2 versicolor
94 5.0 2.3 3.3 1.0 versicolor
95 5.6 2.7 4.2 1.3 versicolor
96 5.7 3.0 4.2 1.2 versicolor
97 5.7 2.9 4.2 1.3 versicolor
98 6.2 2.9 4.3 1.3 versicolor
99 5.1 2.5 3.0 1.1 versicolor
100 5.7 2.8 4.1 1.3 versicolor
101 6.3 3.3 6.0 2.5 virginica
102 5.8 2.7 5.1 1.9 virginica
103 7.1 3.0 5.9 2.1 virginica
104 6.3 2.9 5.6 1.8 virginica
105 6.5 3.0 5.8 2.2 virginica
106 7.6 3.0 6.6 2.1 virginica
107 4.9 2.5 4.5 1.7 virginica
108 7.3 2.9 6.3 1.8 virginica
109 6.7 2.5 5.8 1.8 virginica
110 7.2 3.6 6.1 2.5 virginica
111 6.5 3.2 5.1 2.0 virginica
112 6.4 2.7 5.3 1.9 virginica
113 6.8 3.0 5.5 2.1 virginica
114 5.7 2.5 5.0 2.0 virginica
115 5.8 2.8 5.1 2.4 virginica
116 6.4 3.2 5.3 2.3 virginica
117 6.5 3.0 5.5 1.8 virginica
118 7.7 3.8 6.7 2.2 virginica
119 7.7 2.6 6.9 2.3 virginica
120 6.0 2.2 5.0 1.5 virginica
121 6.9 3.2 5.7 2.3 virginica
122 5.6 2.8 4.9 2.0 virginica
123 7.7 2.8 6.7 2.0 virginica
124 6.3 2.7 4.9 1.8 virginica
125 6.7 3.3 5.7 2.1 virginica
126 7.2 3.2 6.0 1.8 virginica
127 6.2 2.8 4.8 1.8 virginica
128 6.1 3.0 4.9 1.8 virginica
129 6.4 2.8 5.6 2.1 virginica
130 7.2 3.0 5.8 1.6 virginica
131 7.4 2.8 6.1 1.9 virginica
132 7.9 3.8 6.4 2.0 virginica
133 6.4 2.8 5.6 2.2 virginica
134 6.3 2.8 5.1 1.5 virginica
135 6.1 2.6 5.6 1.4 virginica
136 7.7 3.0 6.1 2.3 virginica
137 6.3 3.4 5.6 2.4 virginica
138 6.4 3.1 5.5 1.8 virginica
139 6.0 3.0 4.8 1.8 virginica
140 6.9 3.1 5.4 2.1 virginica
141 6.7 3.1 5.6 2.4 virginica
142 6.9 3.1 5.1 2.3 virginica
143 5.8 2.7 5.1 1.9 virginica
144 6.8 3.2 5.9 2.3 virginica
145 6.7 3.3 5.7 2.5 virginica
146 6.7 3.0 5.2 2.3 virginica
147 6.3 2.5 5.0 1.9 virginica
148 6.5 3.0 5.2 2.0 virginica
149 6.2 3.4 5.4 2.3 virginica
150 5.9 3.0 5.1 1.8 virginica
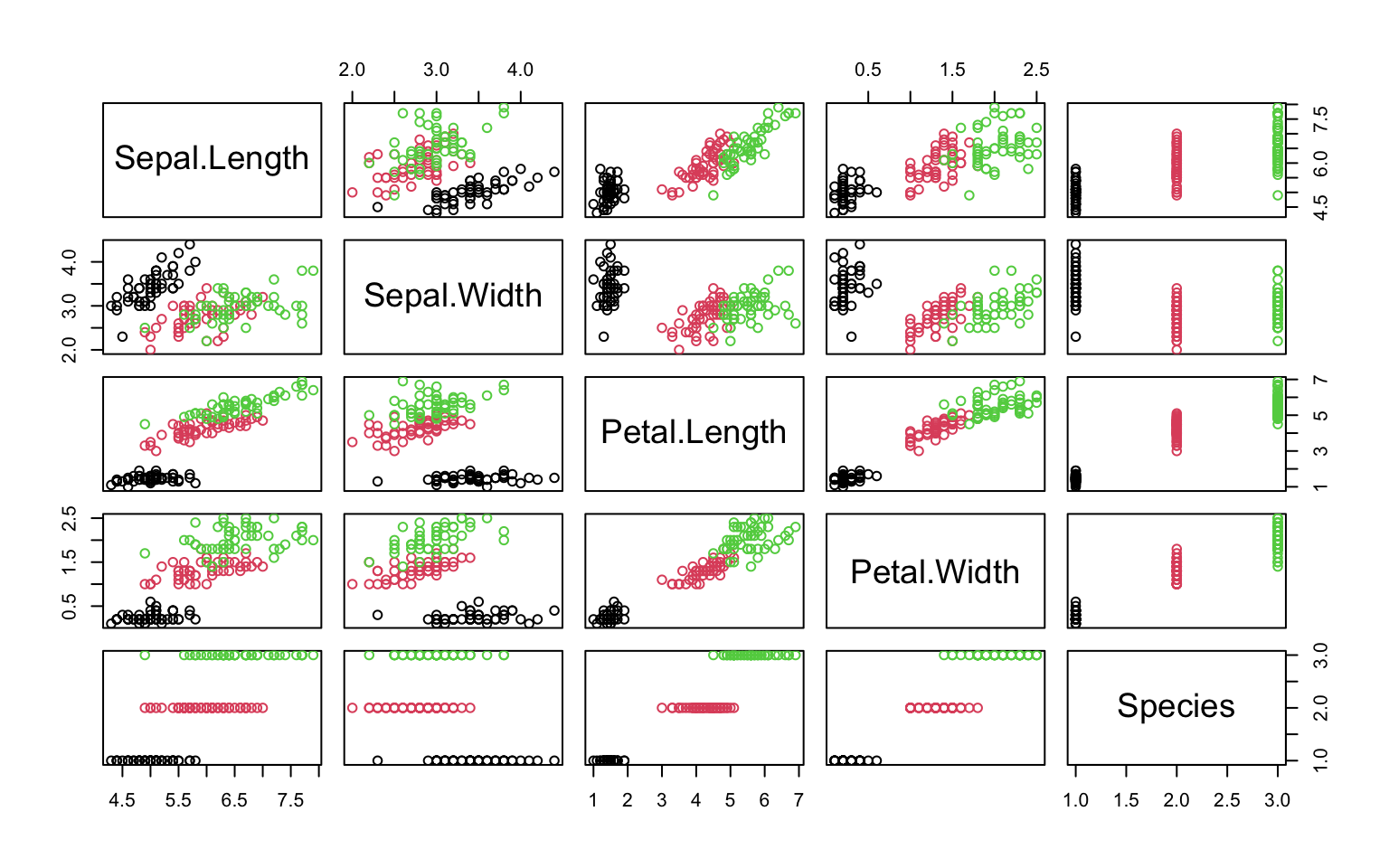
pairs(iris, col = iris$Species)
FactoMineR::PCA(iris, quali.sup=5, graph=F) %>%
factoextra::fviz_pca_biplot(.,
addEllipses=T,
habillage=iris$Species,
col.var="black")
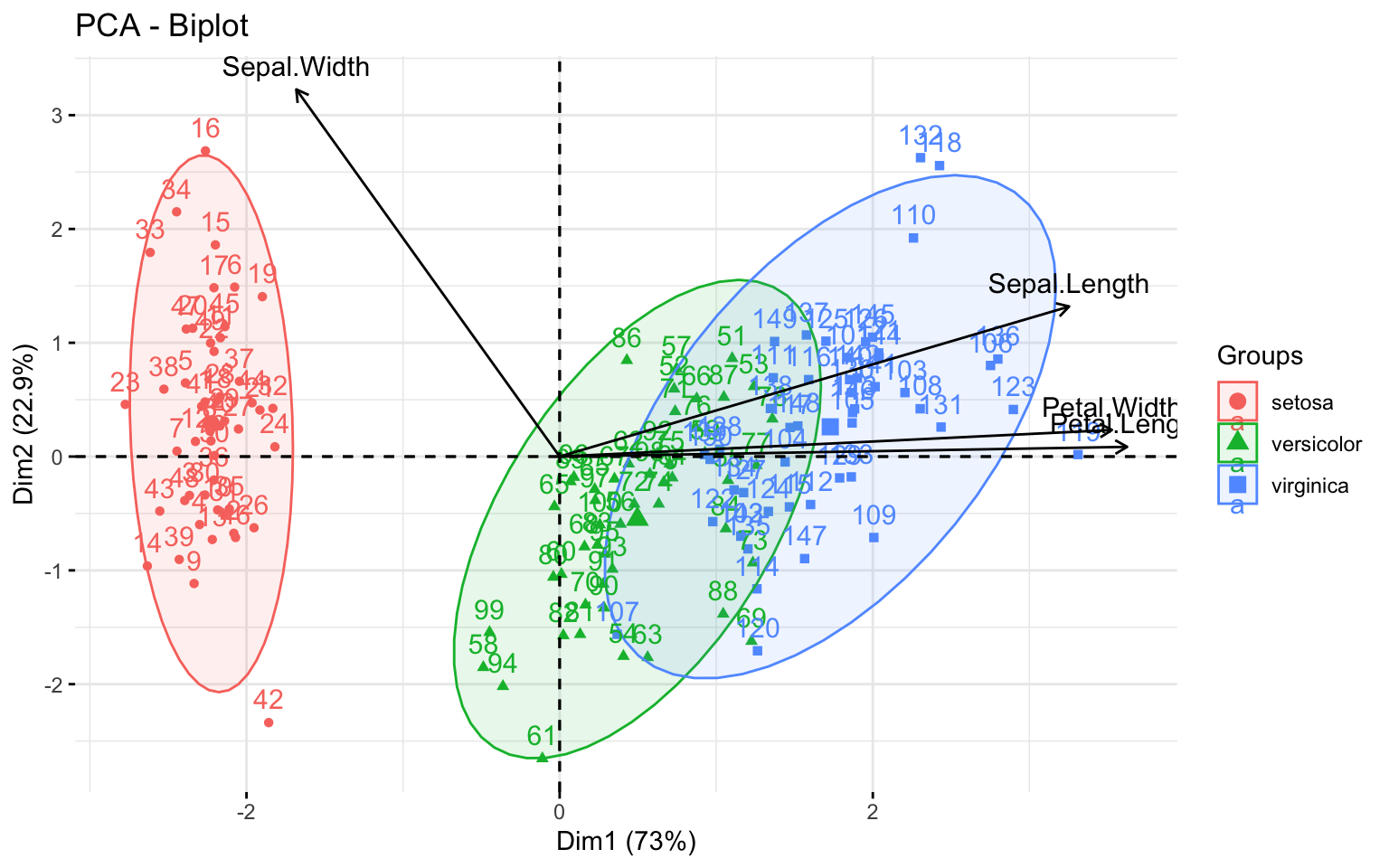
L’ACP et la matrice de corrélation montrent une bonne distinction entre les espèces, via les mesures des pétales. Toutefois, une confusion possible est visible entre I. virginica et I. versicolor.
Pour prédire les espèces et explorer différentes manières de discriminer des facteurs, allons voir différents algorithmes de classification.
Classification non supervisée
K-means
Génère des coordonnées aléatoirement, puis leur grèffe les observations les plus proches. Plusieurs itérations permettent de converger vers une solution qui permet de :
-
Regrouper des observations similaires: L’algorithme K-means identifie des patterns dans les données en regroupant les observations les plus similaires ensemble.
-
Minimiser la distance intra-groupe: Les points associés à chaque groupe (cluster) sont le plus près possible les uns des autres (forte cohésion), généralement estimé par distance Euclidienne.
-
Maximiser la distance inter-groupe: Les points de différents groupes doivent être le plus loin poissible des autres groupes.
# faire un classement K-means très simple et plus complexe
# K = 3, comme 3 espèces sont attendues
km1 = kmeans(iris[,-5], 3, iter.max = 2)
km2 = kmeans(iris[,-5], 3, iter.max = 10, nstart = 10)
# pour visualiser l'ensemble
g1 = iris %>%
ggplot(aes(x=Petal.Length,y=Sepal.Length, col=Species))+
geom_point()+
ggtitle("Observed")
g2 = iris %>%
ggplot(aes(x=Petal.Length,y=Sepal.Length, col=as.factor(km1$cluster)))+
geom_point()+
ggtitle("K-means")
g3 = iris %>%
ggplot(aes(x=Petal.Length,y=Sepal.Length, col=as.factor(km2$cluster)))+
geom_point()+
ggtitle("K-means tuned")
ggarrange(g1,g2,g3, ncol=3, legend = "none")
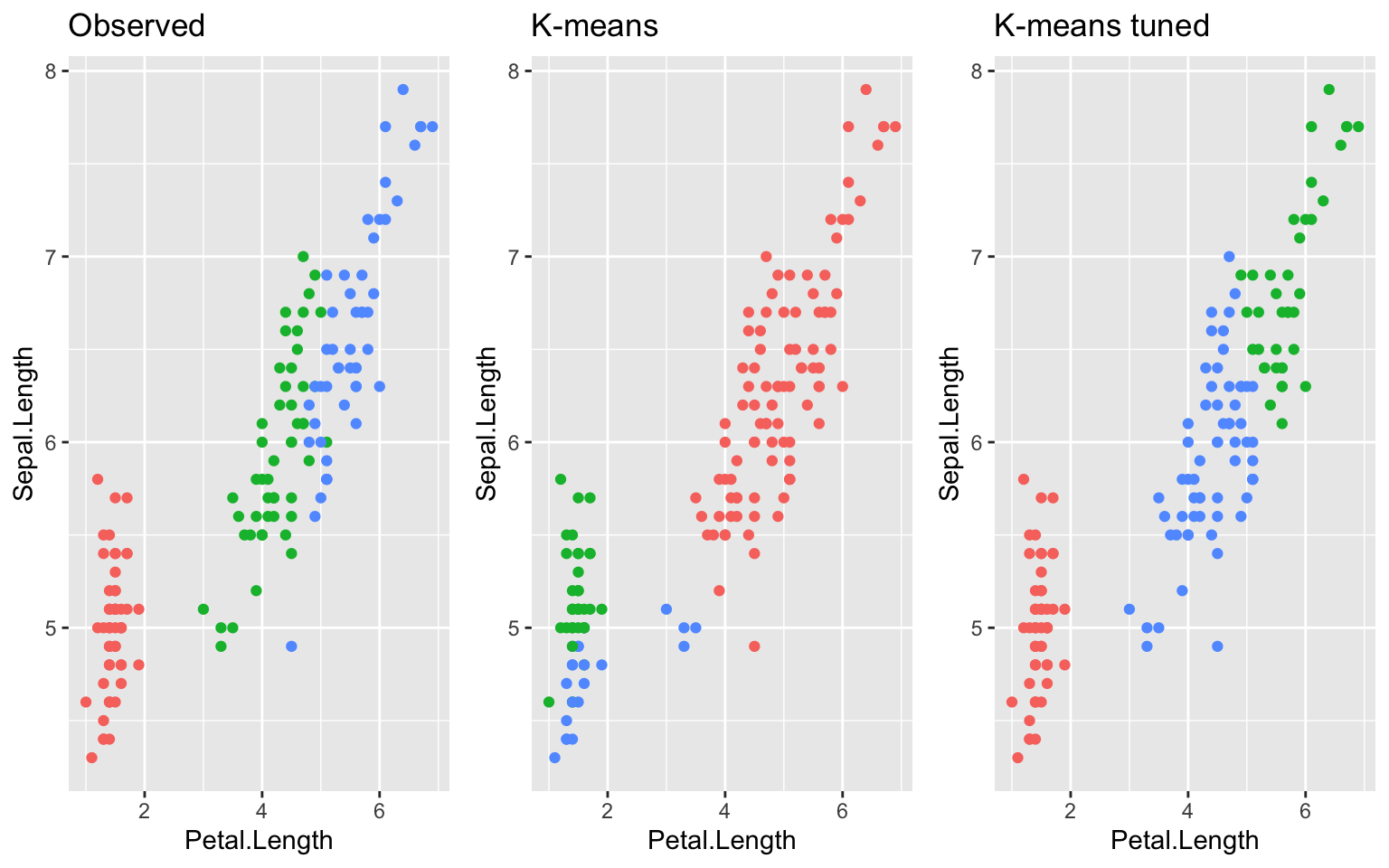
… mais K-means ne nuance pas bien la limite entre deux classes.
Hierarchical clustering
Pour regrouper les observations, un groupe par observation est formé, puis la paire d’observations les plus similaires sont groupées itérativement jusqu’à obtenir un seul groupe. Il suffit alors de couper l’arbre de regroupements au nombre de groupe restant souhaité.
d = dist(iris[,1:4])
h = hclust(d)
plot(h)
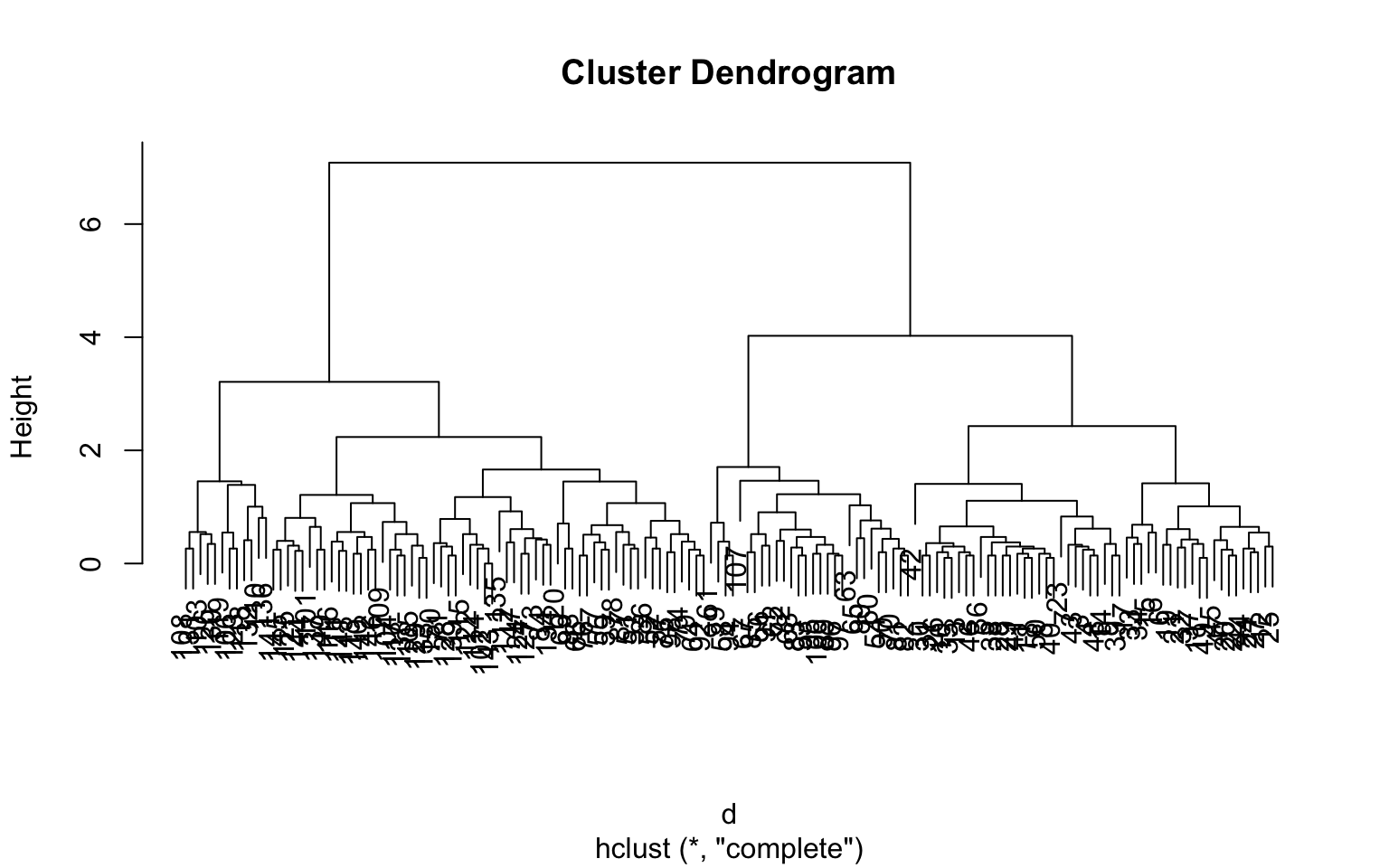
hc = cutree(h, k=3)
g4 = iris %>%
ggplot(aes(x=Petal.Length, y=Sepal.Length, col=as.factor(hc)))+
geom_point()+
ggtitle("Hclustering")
ggarrange(g1,g3,g4, ncol=3, legend = "none")
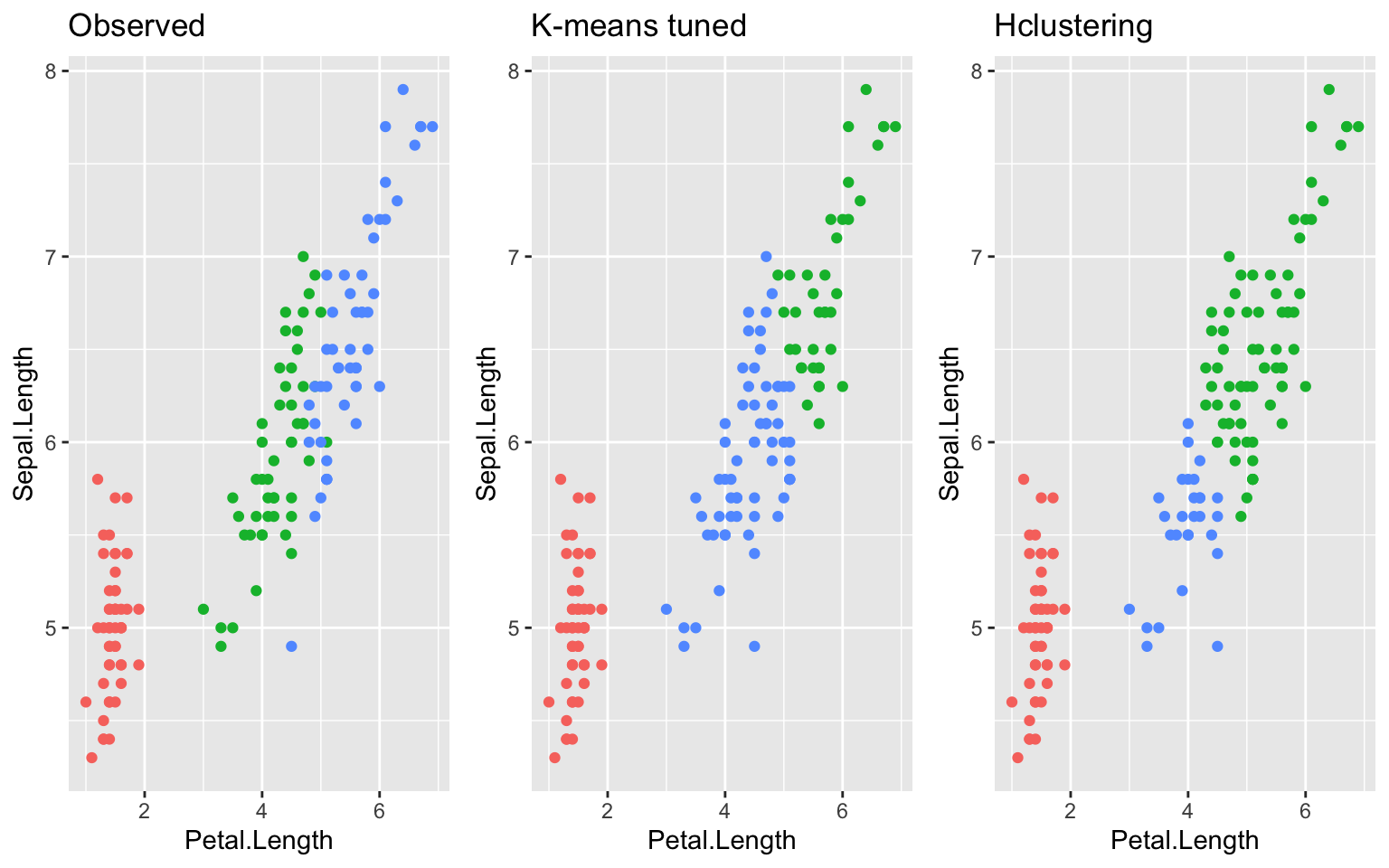
… Encore une fois, incapable de nuancer la séparation entre les espèces.
Classification Supervisée
Implique deux étapes : entrainement et prédiction. Basé sur quelques observations, peut-on prédire d’autres individus? Ces méthodes permettent généralement de meilleur performance et l’établissement de règles complexes, associées au machine learning. Toutefois, les modèles deviennent susceptibles au sur-ajustement (overfit), soit la détection de patrons très forts mais artificiels qui ne sont pas associés à la variation naturelle des données.
K nearest neighbors (kNN)
Pour chaque observation d’entrainement, les k plus proches voisins sont trouvés. La fréquence relative d’appartenance de chaque points à une classe permet d’obtenir un score de probabilité pour la classification.
exemple simple:
train = sample(150, 0.5*150) # séparer les données en échantillon d'entrainement et de test. la proportion classique est 0.7, mais comme l'exemple est simple, utilisons 0.5 pour défavoriser l'algorithme.
knn1 = class::knn(train = iris[train,-5],
test = iris[-train, -5],
cl = iris[train, 5])
knn1 # sortie du modèle
[1] setosa setosa setosa setosa setosa setosa
[7] setosa setosa setosa setosa setosa setosa
[13] setosa setosa setosa setosa setosa setosa
[19] setosa setosa setosa setosa setosa versicolor
[25] versicolor versicolor versicolor versicolor versicolor versicolor
[31] virginica versicolor virginica versicolor versicolor versicolor
[37] versicolor virginica versicolor versicolor versicolor versicolor
[43] versicolor versicolor versicolor versicolor versicolor virginica
[49] virginica virginica virginica versicolor virginica virginica
[55] virginica virginica virginica virginica virginica virginica
[61] virginica virginica virginica virginica virginica virginica
[67] virginica virginica virginica virginica virginica virginica
[73] virginica virginica virginica
Levels: setosa versicolor virginica
table(knn1, iris[-train,5]) # matrice de confusion
knn1 setosa versicolor virginica
setosa 23 0 0
versicolor 0 21 1
virginica 0 3 27
# calcul de l'accuracy (%)
sum(knn1==iris[-train,5]) / sum(table(knn1, iris[-train,5]))
[1] 0.9466667
En manipulant les arguments de la fonction, il est possible d’augmenter la sensibilité du modèle. Nottament, en augmentant le nombre de voisins considérés (k=1 par défaut) et en extrayant la probabilité associée.
knn2 = class::knn(train = iris[train,-5],
test = iris[-train, -5],
cl = iris[train, 5],
k = 10,
prob = T)
cm = table(knn2, iris[-train,5]) # définir la matrice de confusion
cm
knn2 setosa versicolor virginica
setosa 23 0 0
versicolor 0 21 2
virginica 0 3 26
sum(diag(cm))/sum(cm) # calcul simple de l'accuracy (%)
[1] 0.9333333
Maintenant que la précision du modèle est évaluée sur des données indépendantes (training vs test), on peut utiliser cette structure de modèle pour prédire l’ensemble des observations.
knn3 = knn(train = iris[train, -5],
test = iris[,-5],
cl= iris[train, 5],
k = 10,
prob = T)
table(knn3, iris[,5])
knn3 setosa versicolor virginica
setosa 50 0 0
versicolor 0 47 5
virginica 0 3 45
g5 = iris %>%
ggplot(aes(x=Petal.Length, y=Sepal.Length,
col=knn3,
alpha = attr(knn3, "prob")))+
geom_point()+
ggtitle("kNN")
ggarrange(g1,g5, ncol=2)
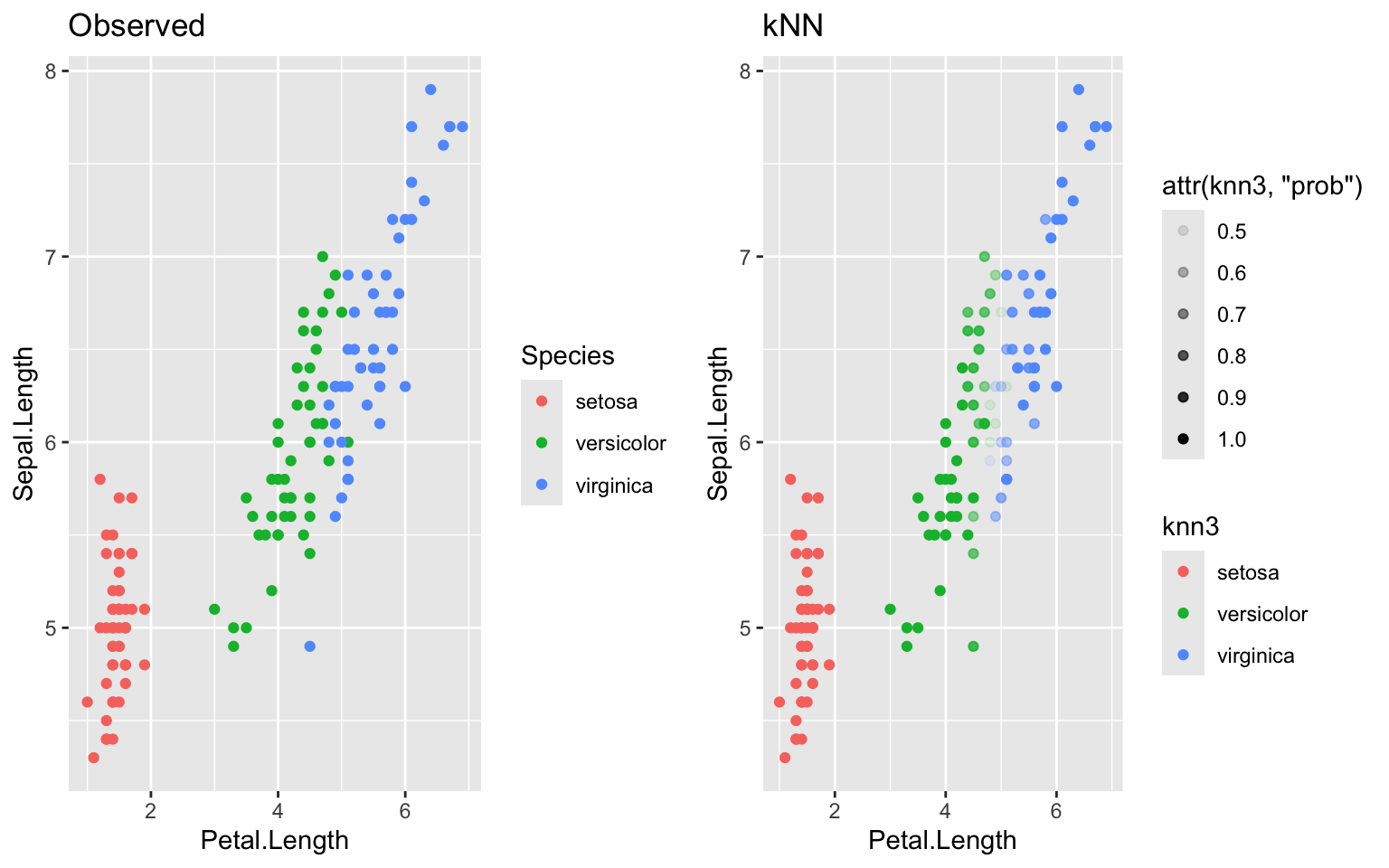
Pour rendre l’exercise de calibration / validation plus robuste (la séparation des données en set d’entrainement vs test, il est possible de faire ce processus à plusieurs reprises, en excluant une fraction définie des données de façon aléatoire et itérative.
Model Performance: cross validation (k-folds)
L’une des méthode de validation croisée des plus fréquentes est la k-folds cross validation. Un nombre K de sous échantillons sont produits dans lesquels une fraction 1/K des observations sont manquantes. La performance moyenne est alors considérée.
Le package caret est le plus utilisé pour la validation et l’ajustement des modèles de ML.
library(caret)
cv1 = caret::train(Species ~ ., iris,
method = "knn",
trControl = trainControl(method="cv",
number = 10,
verboseIter = F))
confusionMatrix(cv1, mode="prec_recall")
Cross-Validated (10 fold) Confusion Matrix
(entries are percentual average cell counts across resamples)
Reference
Prediction setosa versicolor virginica
setosa 33.3 0.0 0.0
versicolor 0.0 31.3 1.3
virginica 0.0 2.0 32.0
Accuracy (average) : 0.9667
cv1
k-Nearest Neighbors
150 samples
4 predictor
3 classes: 'setosa', 'versicolor', 'virginica'
No pre-processing
Resampling: Cross-Validated (10 fold)
Summary of sample sizes: 135, 135, 135, 135, 135, 135, ...
Resampling results across tuning parameters:
k Accuracy Kappa
5 0.9600000 0.94
7 0.9600000 0.94
9 0.9666667 0.95
Accuracy was used to select the optimal model using the largest value.
The final value used for the model was k = 9.
Bien que kNN soit relativement performant, sa complexité limitée n’est pas très performante pour établir des règles complexes dans des contextes écologiques souvent non linéaires. Pour ce faire, des méthodes arborescentes sont souvent utilisées.
Arbres décisionnels (Decision Trees)
La forme la plus simple d’algorithme arborescent de classification supervisée.
Les DTs séparent successivement les observations en deux groupes qui maximisent les différences à l’aide d’une règle ifelse, jusqu’à l’obtention de noeuds/nodes de fin (feuilles/leaves) homogènes. Pour éviter le sur-ajustement, l’utilisation de validation croisée et la séparation de la base de données sont recommendés, mais il est également possible de limiter la profondeur de l’arbre, en limitant son nombre de séparations.
library(rpart)
library(rpart.plot)
dt1 = rpart(Species ~ ., data=iris,
method="class")
rpart.plot(dt1)
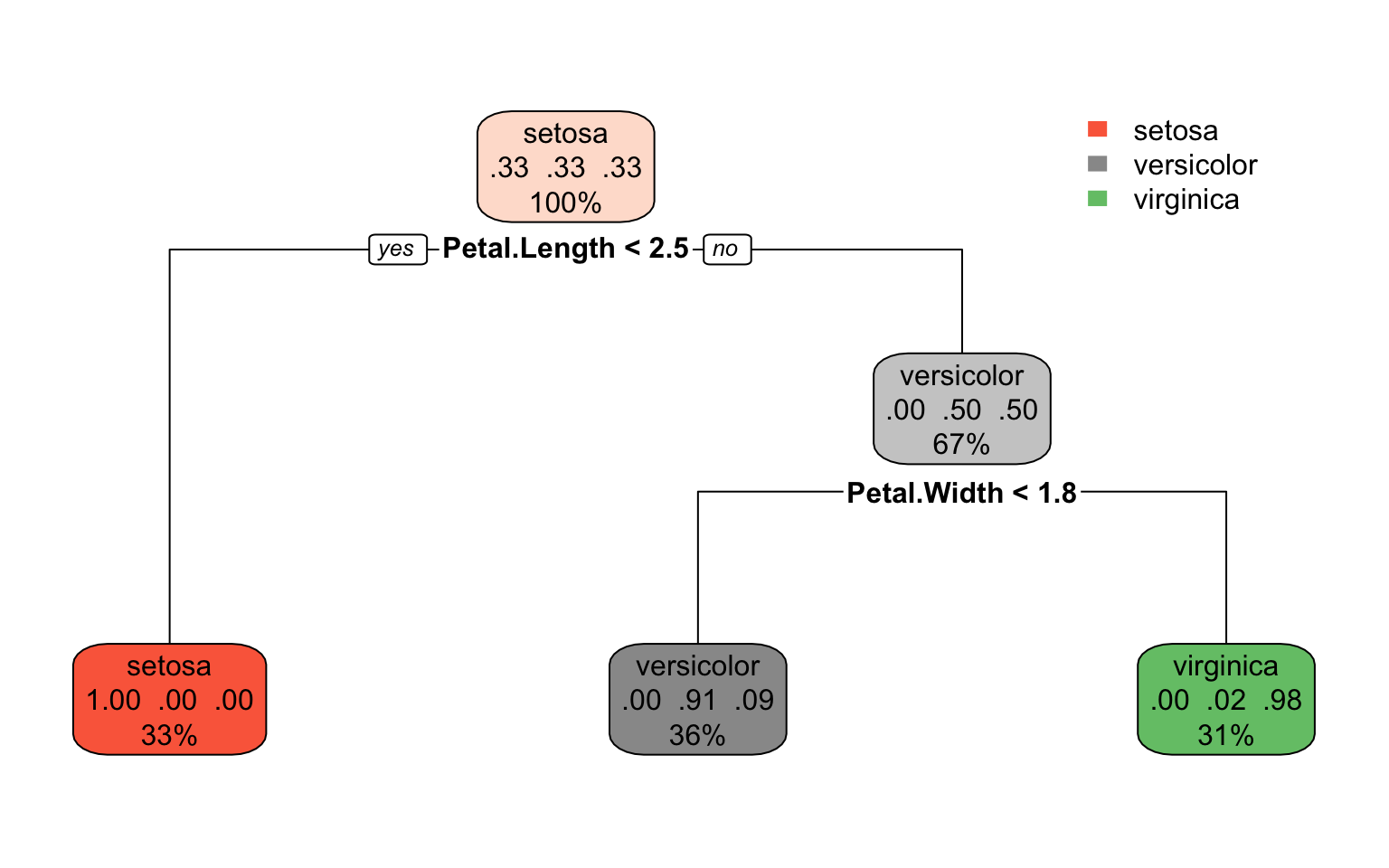
table(predict(dt1, iris, type="class"),iris$Species)
setosa versicolor virginica
setosa 50 0 0
versicolor 0 49 5
virginica 0 1 45
La manière la plus répandue d’éffectuer la validation croisée est de réaliser un grand nombre d’arbres de décisions qui se basent sur un fraction des observations, et un sous-ensemble de prédicteurs puis d’en extraire un arbre moyen. C’est le concepte derrière les Random Forest.
Méthodes d’ensembles
RF: Random Forests
Différents packages existent pour effectuer les random forest dans R. Cet atelier se limitera à l’utilisation de ranger.
library(ranger)
L’utilisation de base de ranger est assez simple. On peut utiliser l’argument importance pour définir un paramètre qui estime l’importance des variables par différentes méthodes.
rf = ranger(Species~., data=iris, importance = "permutation")
rf
Ranger result
Call:
ranger(Species ~ ., data = iris, importance = "permutation")
Type: Classification
Number of trees: 500
Sample size: 150
Number of independent variables: 4
Mtry: 2
Target node size: 1
Variable importance mode: permutation
Splitrule: gini
OOB prediction error: 4.00 %
rf$confusion.matrix
predicted
true setosa versicolor virginica
setosa 50 0 0
versicolor 0 47 3
virginica 0 3 47
g6 = iris %>%
mutate(Predictions = predictions(stats::predict(rf, iris))) %>%
ggplot(aes(x=Petal.Length, y=Sepal.Length,
col=Predictions))+
geom_point()+
ggtitle("Random Forest")
ggarrange(g1,g6)
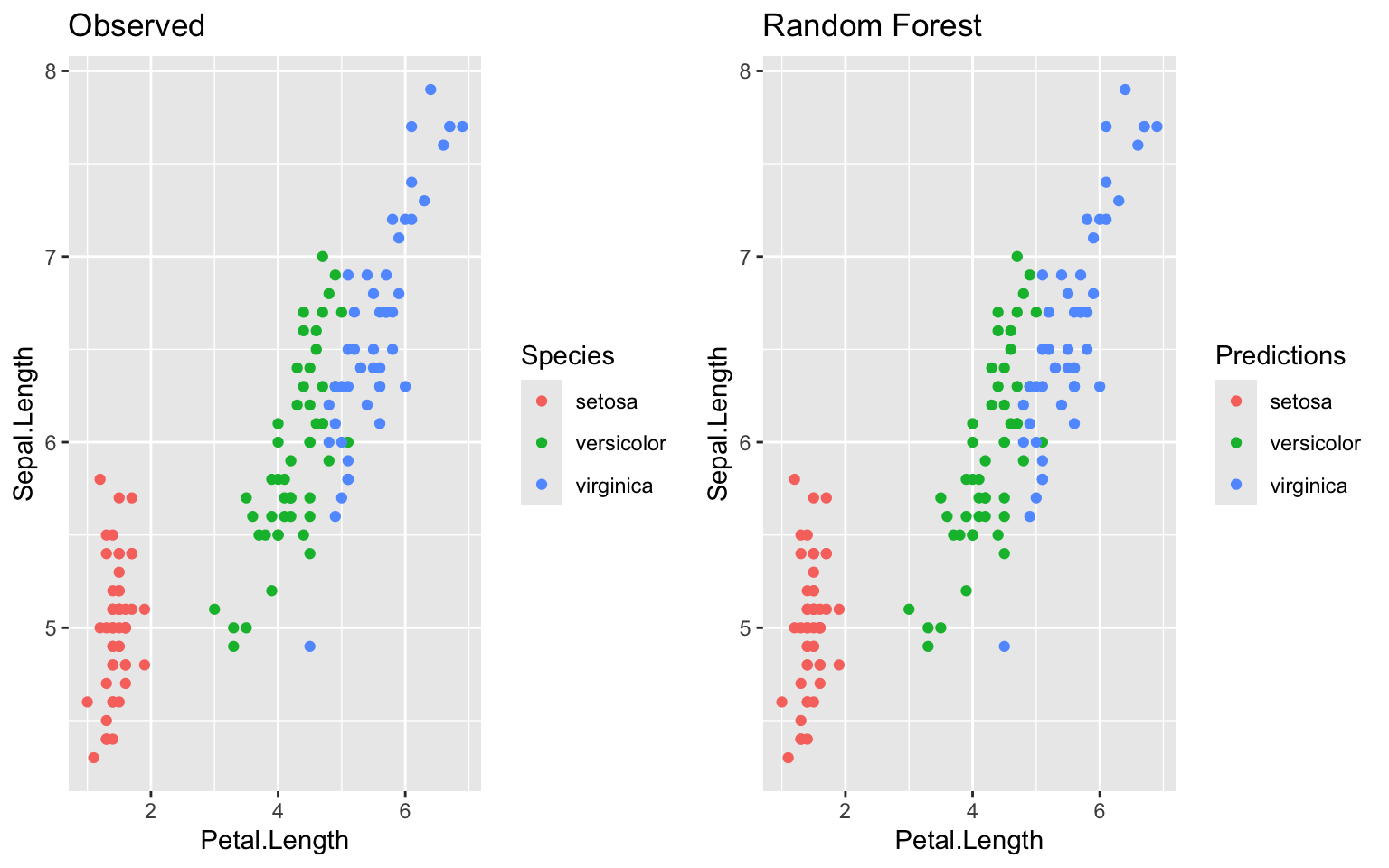
importance = data.frame(name = names(rf$variable.importance),
value = rf$variable.importance)
ggplot(importance, aes(x = reorder(name, -value), y = value)) +
geom_bar(stat = "identity", fill = "steelblue") +
labs(x = "Name", y = "Value", title = "Most important predictors") +
theme_minimal() +
theme(axis.text.x = element_text(angle = 45, hjust = 1))
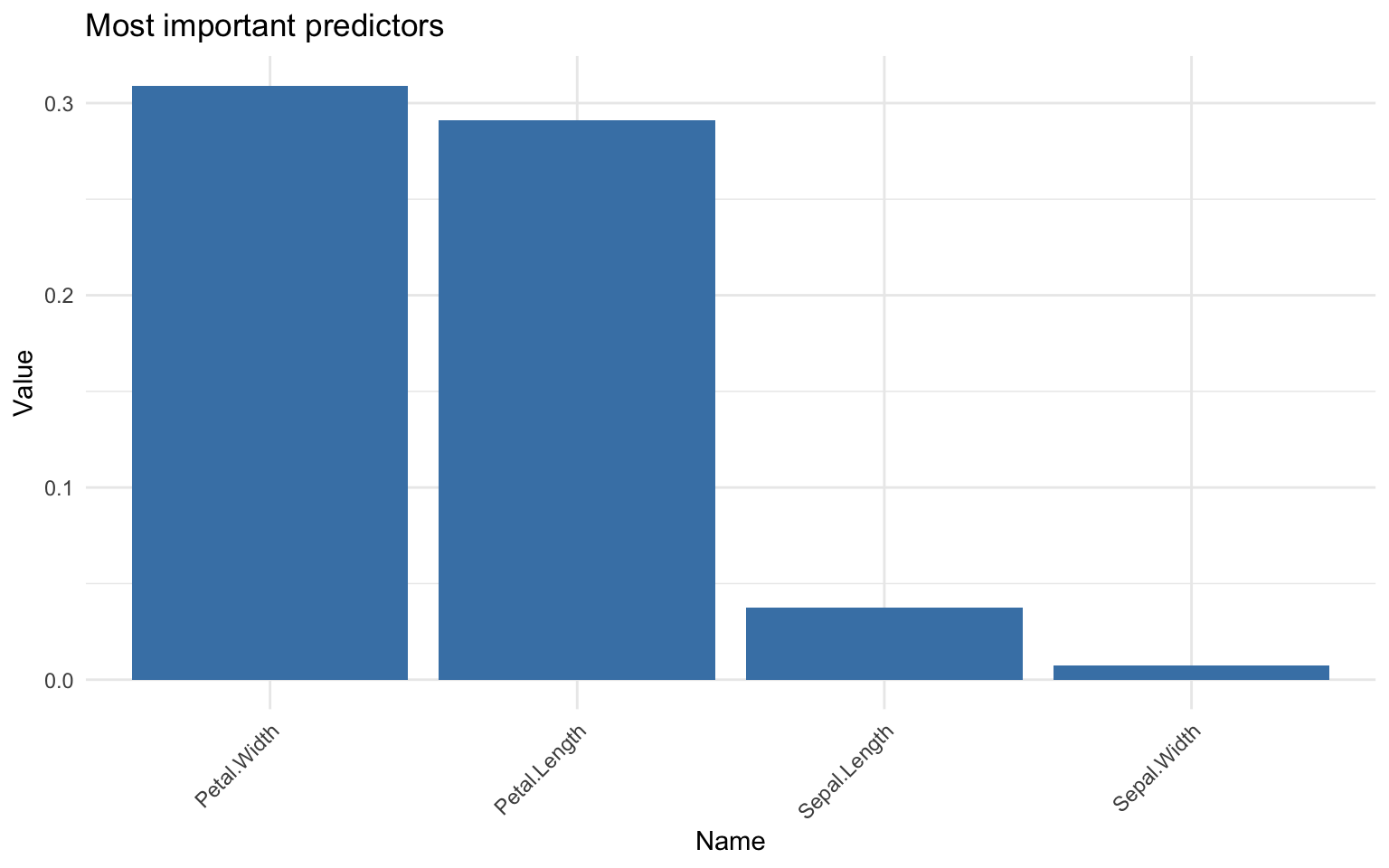
Les RF sont des outils puissants qui sont particulièrement utiles dans bases de données très complexes… Ce qui n’est pas le cas avec iris.
Exemple #2
Classification d’une cible de sonar selon l’énergie captée par bandes de fréquences :
-
beaucoup de prédicteur assez abstraits, difficile à sélectionner via des hypothèses
-
difficile d’inférer sur l’indépendance des variables
-
Exploration inconcluante
library(mlbench)
data(Sonar)
# View(Sonar)
# R for Rock, # M for Metal
FactoMineR::PCA(Sonar, quali.sup=61, graph=F) %>%
factoextra::fviz_pca_biplot(.,
addEllipses=T,
habillage=Sonar$Class,
col.var="black")
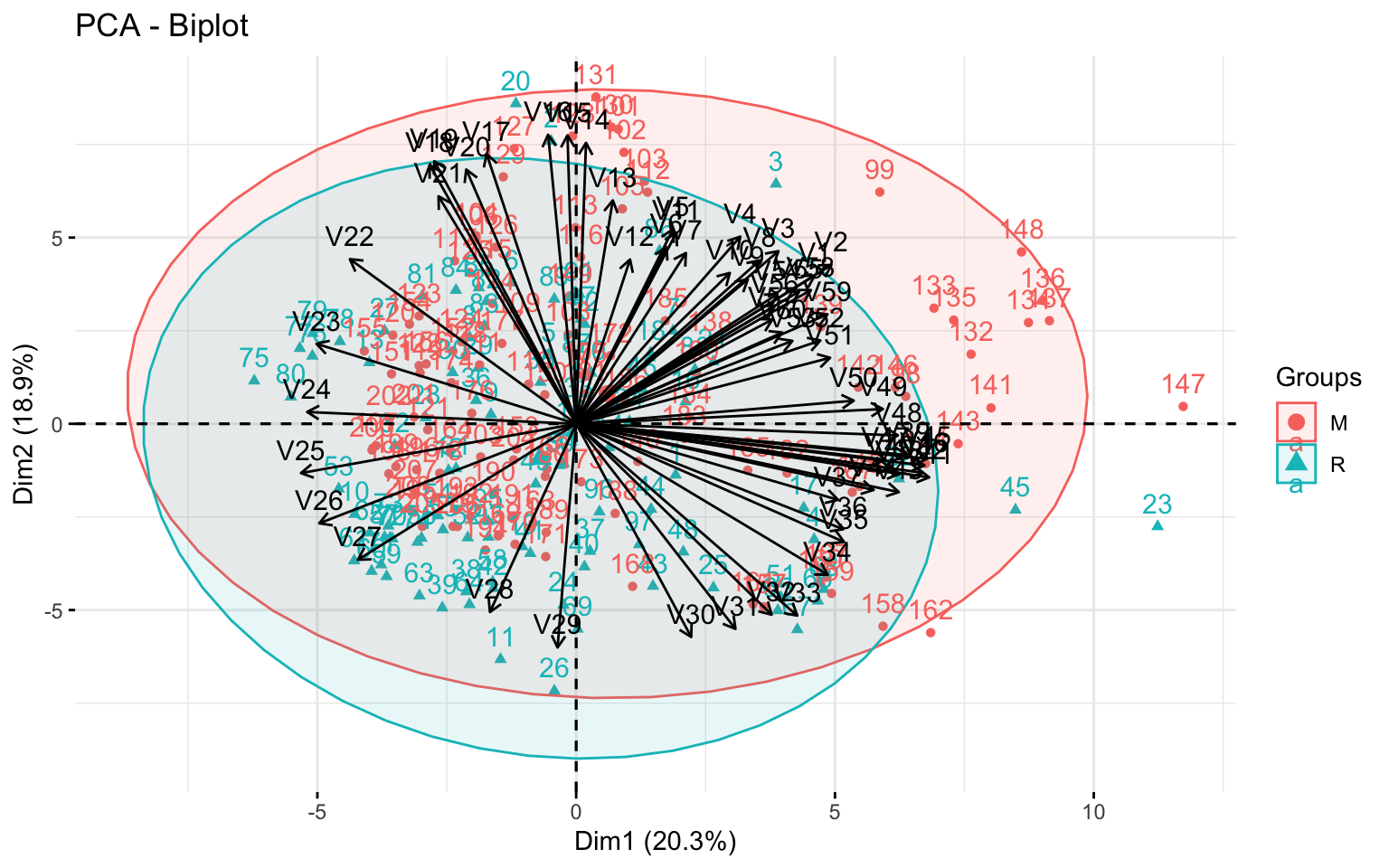
À première vue, aucunes règles ne permettent de bien distinguer les deux classes: M et R. Le machine learning peut-il augmenter notre capacité à distinguer les classes?
dt2 = rpart(Class ~., data=Sonar,
method="class")
rpart.plot(dt2)
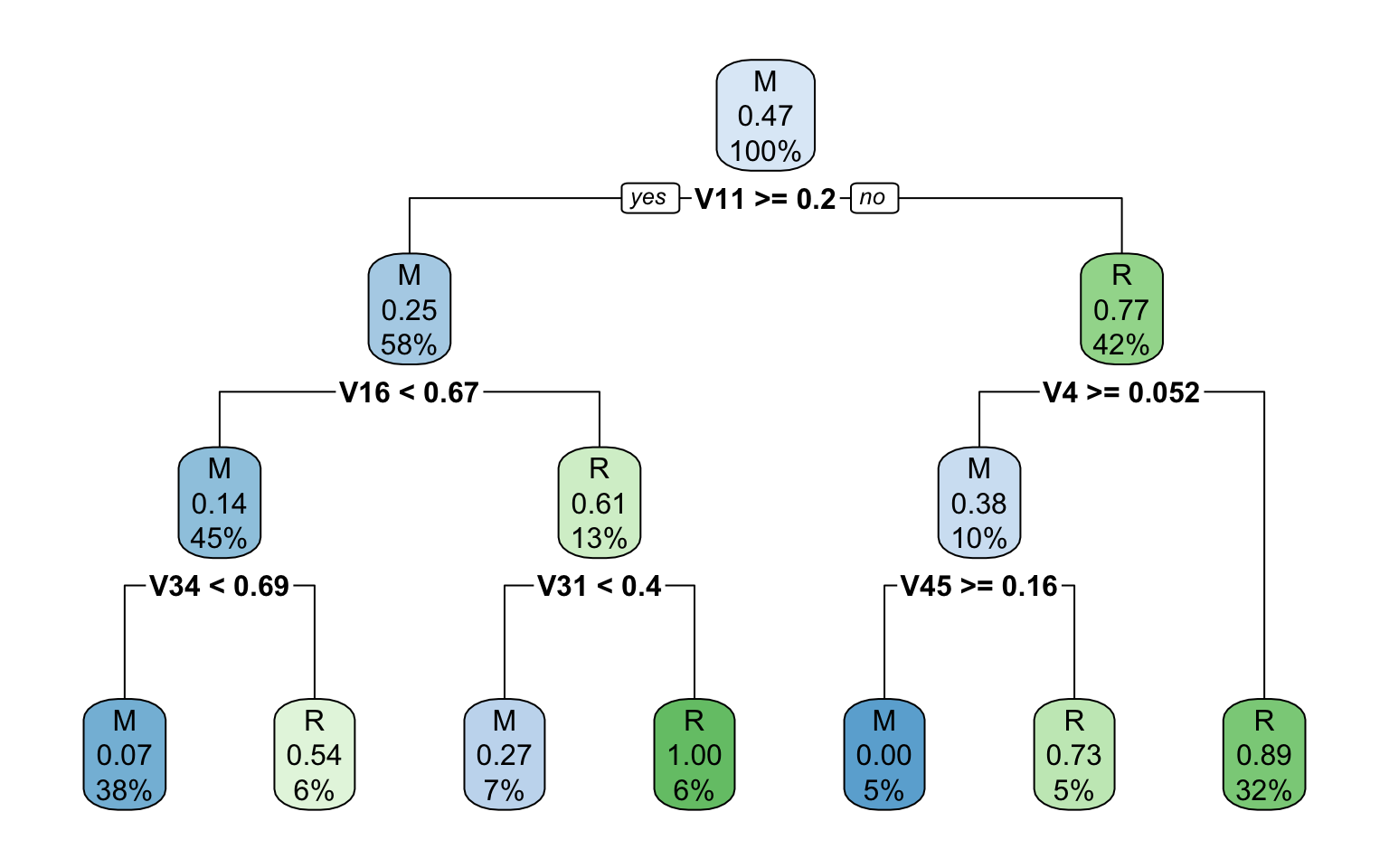
table(predict(dt2, Sonar, type="class"),Sonar$Class)
M R
M 95 10
R 16 87
Un simple arbre décisionnel semble obtenir des prédictions relativement bonnes. Qu’en est-il des méthodes d’ensemble?
Ajustement de Random Forests et sélection de modèles
rf1 = ranger(Class ~ ., data=Sonar)
rf1
Ranger result
Call:
ranger(Class ~ ., data = Sonar)
Type: Classification
Number of trees: 500
Sample size: 208
Number of independent variables: 60
Mtry: 7
Target node size: 1
Variable importance mode: none
Splitrule: gini
OOB prediction error: 13.94 %
Le OOB (out-of-bag) prediction error est de 14.9 %, signifiant une erreur de prédiction moyenne de 14.9% sur les observations non incluent dans l’arbre effectuant la prédiction.
Peut-on augmenter les performances?
# utilison la fonction train de caret
rf2 = train(Class ~., data=Sonar,
method = "ranger",
tuneLength = 3, # essayer 3 valeurs par paramètre clé
trControl = trainControl(method="cv", #crossvalidation
number = 5, #5-folds
verboseIter = F))
rf2
Random Forest
208 samples
60 predictor
2 classes: 'M', 'R'
No pre-processing
Resampling: Cross-Validated (5 fold)
Summary of sample sizes: 166, 167, 167, 167, 165
Resampling results across tuning parameters:
mtry splitrule Accuracy Kappa
2 gini 0.8363369 0.6663303
2 extratrees 0.8413257 0.6761440
31 gini 0.7985577 0.5896803
31 extratrees 0.8754612 0.7474313
60 gini 0.7940226 0.5812744
60 extratrees 0.8566351 0.7091756
Tuning parameter 'min.node.size' was held constant at a value of 1
Accuracy was used to select the optimal model using the largest value.
The final values used for the model were mtry = 31, splitrule = extratrees
and min.node.size = 1.
plot(rf2)
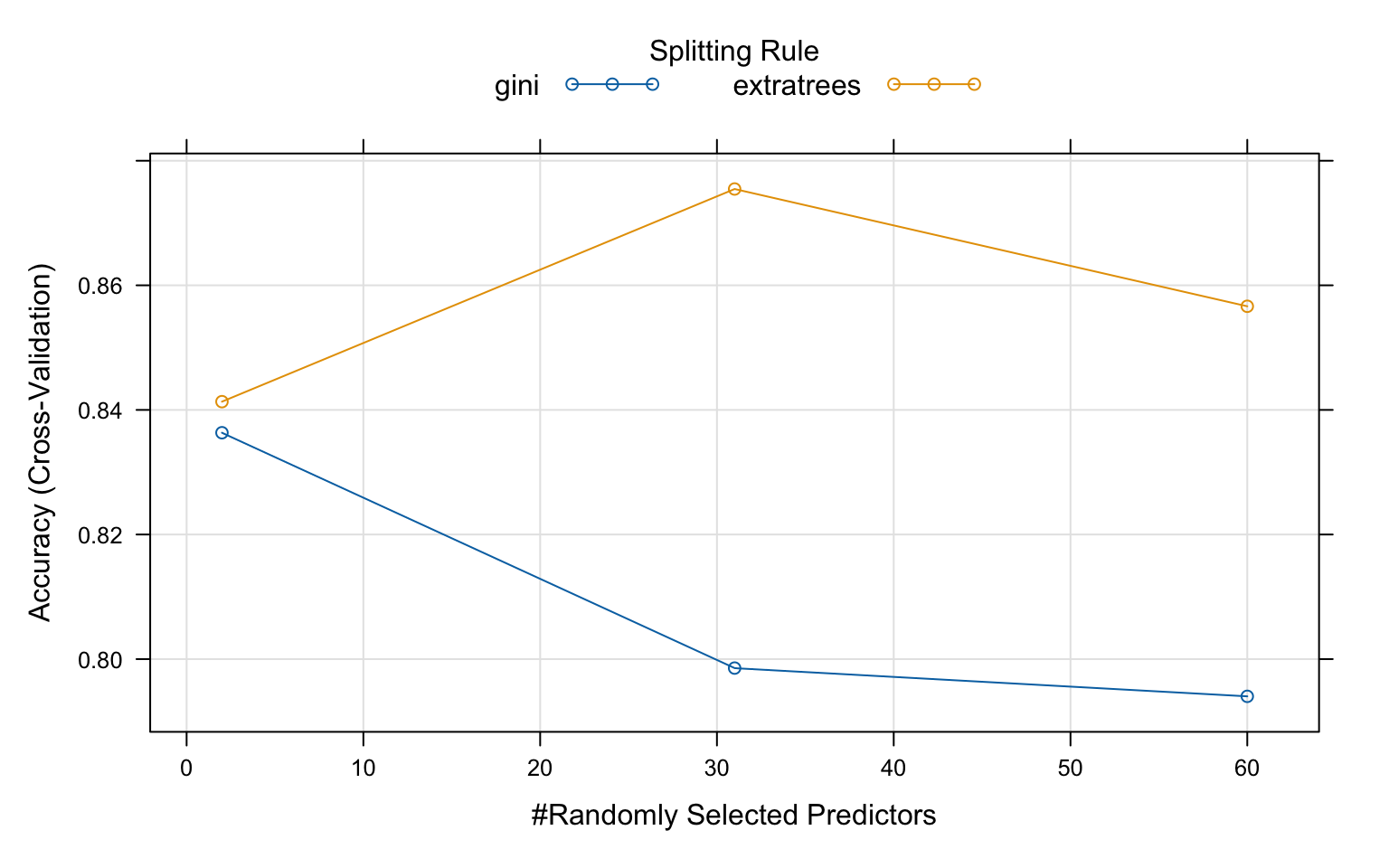
rf2$finalModel
Ranger result
Call:
ranger::ranger(dependent.variable.name = ".outcome", data = x, mtry = min(param$mtry, ncol(x)), min.node.size = param$min.node.size, splitrule = as.character(param$splitrule), write.forest = TRUE, probability = classProbs, ...)
Type: Classification
Number of trees: 500
Sample size: 208
Number of independent variables: 60
Mtry: 31
Target node size: 1
Variable importance mode: none
Splitrule: extratrees
Number of random splits: 1
OOB prediction error: 12.98 %
L’ajustement automatisé du modèle permet de gagner en performances en manipulant le nombre de variable par arbre ainsi que la règle de séparation des noeuds.
Il est possible de spécifier manuellement des hyper-paramètres à tester. La sélection d’hyper-paramètres est une question d’expérience, d’essai-erreur et de contraintes spécifiques à la question de recherche… ou de temps de calcul. il faut être prudent dans le nombre de paramètres à essayer, car le temps de calcul peut augmenter exponentiellement.
tgrid <- expand.grid(
.mtry = c(5, 10, 30), # valeurs de mtry à tester
.splitrule = c("gini","extratrees"), # types de splitrules à tester
.min.node.size = c(1,3,5) # valeurs de min.node.size à tester
)
tune_rf = train(Class ~ .,
data = Sonar,
method = "ranger",
trControl = trainControl(method="cv",
number = 3,
verboseIter = T),
tuneGrid = tgrid,
num.trees= 1000, # augmentation du nombre d'arbres
importance = "permutation")
+ Fold1: mtry= 5, splitrule=gini, min.node.size=1
- Fold1: mtry= 5, splitrule=gini, min.node.size=1
+ Fold1: mtry=10, splitrule=gini, min.node.size=1
- Fold1: mtry=10, splitrule=gini, min.node.size=1
+ Fold1: mtry=30, splitrule=gini, min.node.size=1
- Fold1: mtry=30, splitrule=gini, min.node.size=1
+ Fold1: mtry= 5, splitrule=extratrees, min.node.size=1
- Fold1: mtry= 5, splitrule=extratrees, min.node.size=1
+ Fold1: mtry=10, splitrule=extratrees, min.node.size=1
- Fold1: mtry=10, splitrule=extratrees, min.node.size=1
+ Fold1: mtry=30, splitrule=extratrees, min.node.size=1
- Fold1: mtry=30, splitrule=extratrees, min.node.size=1
+ Fold1: mtry= 5, splitrule=gini, min.node.size=3
- Fold1: mtry= 5, splitrule=gini, min.node.size=3
+ Fold1: mtry=10, splitrule=gini, min.node.size=3
- Fold1: mtry=10, splitrule=gini, min.node.size=3
+ Fold1: mtry=30, splitrule=gini, min.node.size=3
- Fold1: mtry=30, splitrule=gini, min.node.size=3
+ Fold1: mtry= 5, splitrule=extratrees, min.node.size=3
- Fold1: mtry= 5, splitrule=extratrees, min.node.size=3
+ Fold1: mtry=10, splitrule=extratrees, min.node.size=3
- Fold1: mtry=10, splitrule=extratrees, min.node.size=3
+ Fold1: mtry=30, splitrule=extratrees, min.node.size=3
- Fold1: mtry=30, splitrule=extratrees, min.node.size=3
+ Fold1: mtry= 5, splitrule=gini, min.node.size=5
- Fold1: mtry= 5, splitrule=gini, min.node.size=5
+ Fold1: mtry=10, splitrule=gini, min.node.size=5
- Fold1: mtry=10, splitrule=gini, min.node.size=5
+ Fold1: mtry=30, splitrule=gini, min.node.size=5
- Fold1: mtry=30, splitrule=gini, min.node.size=5
+ Fold1: mtry= 5, splitrule=extratrees, min.node.size=5
- Fold1: mtry= 5, splitrule=extratrees, min.node.size=5
+ Fold1: mtry=10, splitrule=extratrees, min.node.size=5
- Fold1: mtry=10, splitrule=extratrees, min.node.size=5
+ Fold1: mtry=30, splitrule=extratrees, min.node.size=5
- Fold1: mtry=30, splitrule=extratrees, min.node.size=5
+ Fold2: mtry= 5, splitrule=gini, min.node.size=1
- Fold2: mtry= 5, splitrule=gini, min.node.size=1
+ Fold2: mtry=10, splitrule=gini, min.node.size=1
- Fold2: mtry=10, splitrule=gini, min.node.size=1
+ Fold2: mtry=30, splitrule=gini, min.node.size=1
- Fold2: mtry=30, splitrule=gini, min.node.size=1
+ Fold2: mtry= 5, splitrule=extratrees, min.node.size=1
- Fold2: mtry= 5, splitrule=extratrees, min.node.size=1
+ Fold2: mtry=10, splitrule=extratrees, min.node.size=1
- Fold2: mtry=10, splitrule=extratrees, min.node.size=1
+ Fold2: mtry=30, splitrule=extratrees, min.node.size=1
- Fold2: mtry=30, splitrule=extratrees, min.node.size=1
+ Fold2: mtry= 5, splitrule=gini, min.node.size=3
- Fold2: mtry= 5, splitrule=gini, min.node.size=3
+ Fold2: mtry=10, splitrule=gini, min.node.size=3
- Fold2: mtry=10, splitrule=gini, min.node.size=3
+ Fold2: mtry=30, splitrule=gini, min.node.size=3
- Fold2: mtry=30, splitrule=gini, min.node.size=3
+ Fold2: mtry= 5, splitrule=extratrees, min.node.size=3
- Fold2: mtry= 5, splitrule=extratrees, min.node.size=3
+ Fold2: mtry=10, splitrule=extratrees, min.node.size=3
- Fold2: mtry=10, splitrule=extratrees, min.node.size=3
+ Fold2: mtry=30, splitrule=extratrees, min.node.size=3
- Fold2: mtry=30, splitrule=extratrees, min.node.size=3
+ Fold2: mtry= 5, splitrule=gini, min.node.size=5
- Fold2: mtry= 5, splitrule=gini, min.node.size=5
+ Fold2: mtry=10, splitrule=gini, min.node.size=5
- Fold2: mtry=10, splitrule=gini, min.node.size=5
+ Fold2: mtry=30, splitrule=gini, min.node.size=5
- Fold2: mtry=30, splitrule=gini, min.node.size=5
+ Fold2: mtry= 5, splitrule=extratrees, min.node.size=5
- Fold2: mtry= 5, splitrule=extratrees, min.node.size=5
+ Fold2: mtry=10, splitrule=extratrees, min.node.size=5
- Fold2: mtry=10, splitrule=extratrees, min.node.size=5
+ Fold2: mtry=30, splitrule=extratrees, min.node.size=5
- Fold2: mtry=30, splitrule=extratrees, min.node.size=5
+ Fold3: mtry= 5, splitrule=gini, min.node.size=1
- Fold3: mtry= 5, splitrule=gini, min.node.size=1
+ Fold3: mtry=10, splitrule=gini, min.node.size=1
- Fold3: mtry=10, splitrule=gini, min.node.size=1
+ Fold3: mtry=30, splitrule=gini, min.node.size=1
- Fold3: mtry=30, splitrule=gini, min.node.size=1
+ Fold3: mtry= 5, splitrule=extratrees, min.node.size=1
- Fold3: mtry= 5, splitrule=extratrees, min.node.size=1
+ Fold3: mtry=10, splitrule=extratrees, min.node.size=1
- Fold3: mtry=10, splitrule=extratrees, min.node.size=1
+ Fold3: mtry=30, splitrule=extratrees, min.node.size=1
- Fold3: mtry=30, splitrule=extratrees, min.node.size=1
+ Fold3: mtry= 5, splitrule=gini, min.node.size=3
- Fold3: mtry= 5, splitrule=gini, min.node.size=3
+ Fold3: mtry=10, splitrule=gini, min.node.size=3
- Fold3: mtry=10, splitrule=gini, min.node.size=3
+ Fold3: mtry=30, splitrule=gini, min.node.size=3
- Fold3: mtry=30, splitrule=gini, min.node.size=3
+ Fold3: mtry= 5, splitrule=extratrees, min.node.size=3
- Fold3: mtry= 5, splitrule=extratrees, min.node.size=3
+ Fold3: mtry=10, splitrule=extratrees, min.node.size=3
- Fold3: mtry=10, splitrule=extratrees, min.node.size=3
+ Fold3: mtry=30, splitrule=extratrees, min.node.size=3
- Fold3: mtry=30, splitrule=extratrees, min.node.size=3
+ Fold3: mtry= 5, splitrule=gini, min.node.size=5
- Fold3: mtry= 5, splitrule=gini, min.node.size=5
+ Fold3: mtry=10, splitrule=gini, min.node.size=5
- Fold3: mtry=10, splitrule=gini, min.node.size=5
+ Fold3: mtry=30, splitrule=gini, min.node.size=5
- Fold3: mtry=30, splitrule=gini, min.node.size=5
+ Fold3: mtry= 5, splitrule=extratrees, min.node.size=5
- Fold3: mtry= 5, splitrule=extratrees, min.node.size=5
+ Fold3: mtry=10, splitrule=extratrees, min.node.size=5
- Fold3: mtry=10, splitrule=extratrees, min.node.size=5
+ Fold3: mtry=30, splitrule=extratrees, min.node.size=5
- Fold3: mtry=30, splitrule=extratrees, min.node.size=5
Aggregating results
Selecting tuning parameters
Fitting mtry = 10, splitrule = extratrees, min.node.size = 1 on full training set
tune_rf$finalModel
Ranger result
Call:
ranger::ranger(dependent.variable.name = ".outcome", data = x, mtry = min(param$mtry, ncol(x)), min.node.size = param$min.node.size, splitrule = as.character(param$splitrule), write.forest = TRUE, probability = classProbs, ...)
Type: Classification
Number of trees: 1000
Sample size: 208
Number of independent variables: 60
Mtry: 10
Target node size: 1
Variable importance mode: permutation
Splitrule: extratrees
Number of random splits: 1
OOB prediction error: 14.90 %
Le tuning manuel des hyper-paramètres résulte encore une fois en un gain de précision selon le OOB prediction error. Mais comment mieux évaluer les performances d’un modèle?
Performance globale:
# Accuracy & Kappa
tune_rf
Random Forest
208 samples
60 predictor
2 classes: 'M', 'R'
No pre-processing
Resampling: Cross-Validated (3 fold)
Summary of sample sizes: 139, 138, 139
Resampling results across tuning parameters:
mtry splitrule min.node.size Accuracy Kappa
5 gini 1 0.7785369 0.5499675
5 gini 3 0.7881297 0.5701508
5 gini 5 0.7736370 0.5410517
5 extratrees 1 0.7979296 0.5896880
5 extratrees 3 0.7932367 0.5811306
5 extratrees 5 0.7979296 0.5902212
10 gini 1 0.7832988 0.5598264
10 gini 3 0.7927536 0.5795916
10 gini 5 0.7783989 0.5508529
10 extratrees 1 0.8122153 0.6196282
10 extratrees 3 0.8074534 0.6090584
10 extratrees 5 0.8026225 0.5991324
30 gini 1 0.7831608 0.5603904
30 gini 3 0.7830918 0.5595916
30 gini 5 0.7831608 0.5598054
30 extratrees 1 0.8025535 0.5985251
30 extratrees 3 0.8121463 0.6187818
30 extratrees 5 0.7975845 0.5875680
Accuracy was used to select the optimal model using the largest value.
The final values used for the model were mtry = 10, splitrule = extratrees
and min.node.size = 1.
# Accuracy = (TP + TN) / (TP + FP + TN + FN)
# Kappa = (total accuracy – random accuracy) / (1- random accuracy)
# Kappa : Important a considérer pour les training set débalancés!
# OOB, nombre moyen d'erreurs de classification / nombre de OOB samples(généralement 30%)
tune_rf$finalModel$prediction.error
[1] 0.1490385
performance spécifique: parfois une classe est plus importante qu’une autre, et parfois cette classe est particulièrement rare dans la base de données. Ces performances sont estimées à partir de la matrice de confusion.
ex. présence de végétation, ou encore présence d’un cancer
tune_rf$finalModel$confusion.matrix
predicted
true M R
M 104 7
R 24 73
# Precision : TP/(TP+FP) taux auquel un positif est vraiment positif
caret::precision(tune_rf$finalModel$confusion.matrix, relevant="R")
[1] 0.7525773
caret::precision(tune_rf$finalModel$confusion.matrix, relevant="M")
[1] 0.9369369
# Recall (Sensitivity) : TP/(TP+FN) taux auquel un positif est détecté
caret::recall(tune_rf$finalModel$confusion.matrix, relevant="R")
[1] 0.9125
caret::recall(tune_rf$finalModel$confusion.matrix, relevant="M")
[1] 0.8125
# F-1 score : 2 * (Precision * Recall) / (Precision + Recall)
caret::F_meas(tune_rf$finalModel$confusion.matrix, beta=1, relevant="R")
[1] 0.8248588
caret::F_meas(tune_rf$finalModel$confusion.matrix, beta=1, relevant="M")
[1] 0.8702929
GBDT: Gradient Boosted Decision Trees (XGBoost)
Similaire à random forest… mais séquentiel! Une suite de décision trees construits sur les résidus des précédents.
xgboost (pour extreme gradient boosting) est devenu un standard de performance en ML et est souvent utilisé dans les solutions gagnantes lors de compétitions de data-hacking. Il n’est toutefois pas garantie que ses résultats soient supérieurs à ceux d’un random forest. Il est généralement bon de comparer les deux approches pour une situation donnée.
library(xgboost)
Attaching package: 'xgboost'
The following object is masked from 'package:dplyr':
slice
index = createDataPartition(Sonar$Class, p = 0.7, list = FALSE)
train_data <- Sonar[index, ]
test_data <- Sonar[-index, ]
# Préparer les données pour XGBoost
train_matrix <- as.matrix(train_data[, -61]) # Exclure la colonne de classe
train_label <- as.numeric(train_data$Class) - 1 # Convertir en 0 et 1
test_matrix <- as.matrix(test_data[, -61])
test_label <- as.numeric(test_data$Class) - 1
# Créer les objets DMatrix
dtrain <- xgb.DMatrix(data = train_matrix, label = train_label)
dtest <- xgb.DMatrix(data = test_matrix, label = test_label)
# Définir les paramètres XGBoost
params <- list(
objective = "binary:logistic", #beaucoup de types disponibles, ex. count:poisson, survival:cox, multi:sofmax, reg:squarelogerror
eval_metric = "error", #évalue en fonction de l'erreur de chaque modèle
max_depth = 6, # profondeur maximale des arbres
eta = 0.2 # taux d'apprentissage
)
# Entraîner le modèle
model <- xgb.train(
booster = "gbtree",
params = params,
data = dtrain,
nrounds = 100,
watchlist = list(train = dtrain, test = dtest),
early_stopping_rounds = 20,
verbose = 1
)
[1] train-error:0.082192 test-error:0.225806
Multiple eval metrics are present. Will use test_error for early stopping.
Will train until test_error hasn't improved in 20 rounds.
[2] train-error:0.034247 test-error:0.177419
[3] train-error:0.006849 test-error:0.161290
[4] train-error:0.000000 test-error:0.145161
[5] train-error:0.000000 test-error:0.161290
[6] train-error:0.000000 test-error:0.129032
[7] train-error:0.000000 test-error:0.129032
[8] train-error:0.000000 test-error:0.096774
[9] train-error:0.000000 test-error:0.064516
[10] train-error:0.000000 test-error:0.080645
[11] train-error:0.000000 test-error:0.112903
[12] train-error:0.000000 test-error:0.112903
[13] train-error:0.000000 test-error:0.096774
[14] train-error:0.000000 test-error:0.112903
[15] train-error:0.000000 test-error:0.112903
[16] train-error:0.000000 test-error:0.112903
[17] train-error:0.000000 test-error:0.112903
[18] train-error:0.000000 test-error:0.112903
[19] train-error:0.000000 test-error:0.112903
[20] train-error:0.000000 test-error:0.112903
[21] train-error:0.000000 test-error:0.129032
[22] train-error:0.000000 test-error:0.129032
[23] train-error:0.000000 test-error:0.129032
[24] train-error:0.000000 test-error:0.129032
[25] train-error:0.000000 test-error:0.112903
[26] train-error:0.000000 test-error:0.112903
[27] train-error:0.000000 test-error:0.129032
[28] train-error:0.000000 test-error:0.129032
[29] train-error:0.000000 test-error:0.129032
Stopping. Best iteration:
[9] train-error:0.000000 test-error:0.064516
model
##### xgb.Booster
raw: 38.4 Kb
call:
xgb.train(params = params, data = dtrain, nrounds = 100, watchlist = list(train = dtrain,
test = dtest), verbose = 1, early_stopping_rounds = 20, booster = "gbtree")
params (as set within xgb.train):
objective = "binary:logistic", eval_metric = "error", max_depth = "6", eta = "0.2", booster = "gbtree", validate_parameters = "TRUE"
xgb.attributes:
best_iteration, best_msg, best_ntreelimit, best_score, niter
callbacks:
cb.print.evaluation(period = print_every_n)
cb.evaluation.log()
cb.early.stop(stopping_rounds = early_stopping_rounds, maximize = maximize,
verbose = verbose)
# of features: 60
niter: 29
best_iteration : 9
best_ntreelimit : 9
best_score : 0.06451613
best_msg : [9] train-error:0.000000 test-error:0.064516
nfeatures : 60
evaluation_log:
iter train_error test_error
<num> <num> <num>
1 0.08219178 0.2258065
2 0.03424658 0.1774194
---
28 0.00000000 0.1290323
29 0.00000000 0.1290323
Sélection du meilleur modèle
# Faire des prédictions sur l'ensemble de test
predicted_classes <- ifelse(predict(model, dtest) > 0.5, "R", "M")
predicted_classes <- ifelse(predict(model, xgb.DMatrix(as.matrix(Sonar[,-61]))) > 0.5, "R", "M")
# Évaluer la performance du modèle
confusion_matrix <- table(Actual = Sonar$Class, Predicted = predicted_classes)
confusion_matrix
Predicted
Actual M R
M 110 1
R 3 94
accuracy <- sum(diag(confusion_matrix)) / sum(confusion_matrix)
accuracy
[1] 0.9807692
# Precision TP/(TP+FP)
caret::precision(confusion_matrix, relevant="R")
[1] 0.9690722
caret::precision(confusion_matrix, relevant="M")
[1] 0.990991
# Recall (Sensitivity) : TP/(TP+FN) taux auquel un positif est détecté
caret::recall(confusion_matrix, relevant="R")
[1] 0.9894737
caret::recall(confusion_matrix, relevant="M")
[1] 0.9734513
# F-1 score : 2 * (Precision * Recall) / (Precision + Recall)
caret::F_meas(confusion_matrix, beta=1, relevant="R")
[1] 0.9791667
caret::F_meas(confusion_matrix, beta=1, relevant="M")
[1] 0.9821429
exemple de tuning des hyper-paramètres (ne pas rouler, très long!)
malgré une certaine erreur estimée, le modèle semble me donner une précision de 100% lors des prédictions…
# RÉDUIRE LA GRILLE, TRÈS LONG
# Définir la grille de paramètres à tester
param_grid <- expand.grid(
nrounds = c(100, 200),
max_depth = c(3, 6),
eta = c(0.01, 0.1,0.2),
gamma = c(0, 0.1),
colsample_bytree = c(0.6, 1.0),
min_child_weight = c(1, 3),
subsample = c(0.6, 1.0)
)
# Configurer le contrôle de l'entraînement
ctrl <- trainControl(
method = "cv",
number = 3,
verboseIter = TRUE,
allowParallel = TRUE
)
# Effectuer la recherche par grille
xgb_model <- train(
x = as.matrix(Sonar[,-61]),
y = as.factor(Sonar$Class),
method = "xgbTree",
trControl = ctrl,
tuneGrid = param_grid,
metric = "Accuracy"
)
xgb_model <- train(
x = as.matrix(Sonar[,-61]),
y = as.factor(Sonar$Class),
method = "xgbTree",
tuneLength = 3,
trControl = trainControl(method="cv",
number = 3,
verboseIter = F),
metric = "error"
)
xgb_model$finalModel
predicted_classes <- predict(xgb_model$finalModel, as.matrix(Sonar[,-61]))
predicted_classes <- ifelse(predict(xgb_model$finalModel, as.matrix(Sonar[,-61])) > 0.5, "M", "R")
# Évaluer la performance du modèle
confusion_matrix <- table(Actual = Sonar$Class, Predicted = predicted_classes)
confusion_matrix
accuracy <- sum(diag(confusion_matrix)) / sum(confusion_matrix)
accuracy
predict(xgb_model$finalModel, dtest)
GOI: Gradient information Optimization
Utile pour les très petits training sets
Gradient Forests
Extension des random forests pour identifier des breaking points dans les variables importantes à des ensemble de variables (ex: communautés)