Les spectres de tailles en écologie

Charles Gagnon

Janvier 2026

Voici les ressources principales sur lesquelles nous nous appuyons pour la réalisation de l’activité:

Introduction

Théorie des spectres de tailles

Le spectre de tailles caractérise la structure d’une communauté écologique en décrivant la distribution de l’abondance (ou de la biomasse) en fonction de la taille corporelle des individus. Ce concept repose sur une théorie : l’abondance des organismes diminue à mesure que leur taille augmente.

Dans les écosystèmes aquatiques, cette relation est particulièrement évidente. La base de la chaîne alimentaire est constituée d’une multitude de petits organismes (phytoplancton, zooplancton), tandis que les niveaux trophiques supérieurs sont occupés par un nombre restreint de grands organismes (grands poissons prédateurs).

Selon la théorie, cette relation inverse entre l’abondance ($N$) et la taille/masse ($m$) suit une loi de puissance (Power Law), exprimée par l’équation :

$N$ = $a$ * $m$^$b$

Où :

Lorsqu’on représente ces données sur une échelle logarithmique (log-log), la relation linéaire apparaît. La pente de cette droite ($b$) devient alors un indicateur synthétique de la structure de la communauté.

Cette distribution est régie par les flux métaboliques entre les différents niveaux trophiques. L’énergie disponible diminue à chaque saut de niveau trophique (pertes par respiration, excrétion, chaleur…). Par conséquent, l’écosystème soutient une biomasse décroissante à mesure que l’on monte dans la chaîne alimentaire.

Une pente plus raide (plus négative) indique un écosystème souvent perturbé, où l’énergie peine à atteindre les grands prédateurs. Il y a donc proportionnellement moins de gros organismes. À l’inverse, une pente plus douce suggère un système capable de soutenir une plus grande biomasse de grands organismes.

Applicabilité de la théorie

• Pression de pêche : La pêche cible souvent les grands prédateurs. Si leur nombre diminue, cela peut libérer une pression de prédation sur les plus petits, modifiant ainsi la pente du spectre. Une pente plus abrupte (un b plus négatif) peut être un signe de pression de pêche accrue.

Dans cet atelier

Nous commencerons par démystifier la logique visuelle et mathématique derrière la création d’un spectre de taille.

Ensuite, nous explorerons les 8 méthodes historiquement développées pour quantifier la pente d’une communauté et apprendrons à les appliquer à nos propres données grâce au package R sizeSpectra.

Nous allons également identifier quelle est la meilleure méthode en fonction du contexte en plus d’explorer un enjeu fondamental associé à l’utilisation de la théorie pour des données empiriques.

Code

Tout au long du processus, nous aurons besoin de deux packages: sizeSpectra et poweRlaw. Installons également les outils essentiels pour la visualisation et le traitement de nos données

install.packages("remotes")    # "remote" est nécessaire pour l'installation du package sizeSpectra
remotes::install_github("andrew-edwards/sizeSpectra")
install.packages("poweRlaw")
library(sizeSpectra)
library(poweRlaw)
library(tidyverse) # Package à installer si ce n'est déjà fait

BLOC A: Création d’un jeu de données théorique

L’étape suivante est de générer un jeu de données théoriques de tailles qui suivent une loi de puissance. L’objet “X” correspond à un vecteur de tailles/masses d’organismes vivants.

n = 1000                  # nombre d'observations
b.known = -2              # valeur de l'exposant (b) connue
xmin.known = 1            # valeur de xmin connue
xmax.known = 1000         # valeur de xmax connue
set.seed(42)              # Pour obtenir les mêmes observations pour chaque code effectué

x = rPLB(n,               #création du vecteur de tailles qui génère des données simulées
         b = b.known,     #qui suivent une loi de puissance.
         xmin = xmin.known,
         xmax = xmax.known)

Visualiser les données générées est une bonne pratique afin de valider la simulation. Examinons la distribution des abondances en fonction des tailles:

dat1 <- data.frame(x = sort(x))

ggplot(dat1, aes(x = x)) +
  geom_histogram(color="black") +
  labs(
       x = "Taille", 
       y = "Nombre d'individus")

`stat_bin()` using `bins = 30`. Pick better value `binwidth`.

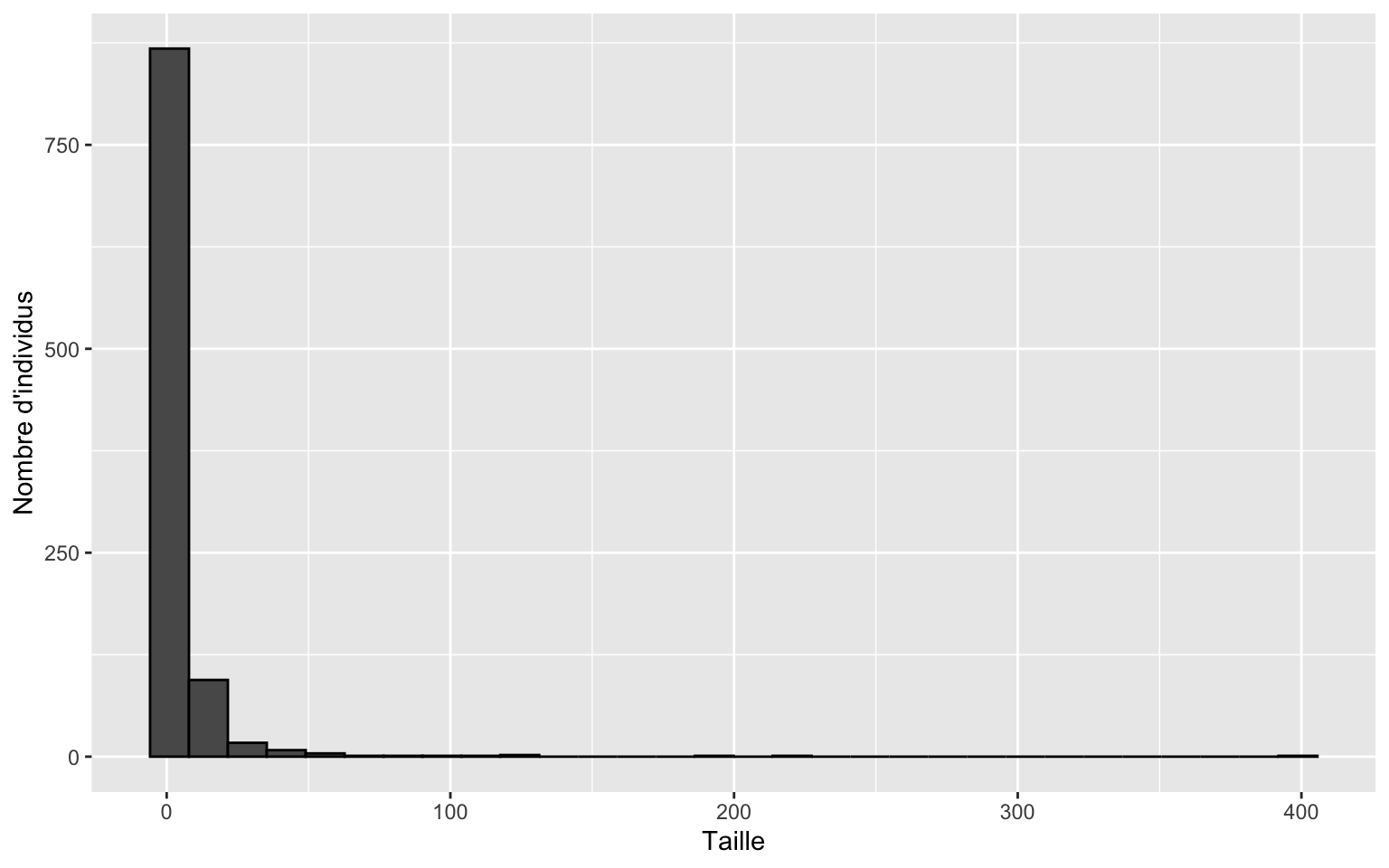
L’histogramme ci-haut n’est pas très informatif. La majorité de la communauté est compressée dans une seule bande. Les gros individus sont très rares. Sur une échelle linéaire, leur fréquence est si basse que les barres correspondantes sont invisibles.

Pour mieux visualiser la structure des données, log-transformons les valeurs de tailles.

ggplot(dat1, aes(x = x)) +
  geom_histogram(color="black") +
  scale_x_log10(labels = function(x) log10(x)) +  
  labs(
       x = "Taille (Log)", 
       y = "Nombre d'individus")

`stat_bin()` using `bins = 30`. Pick better value `binwidth`.

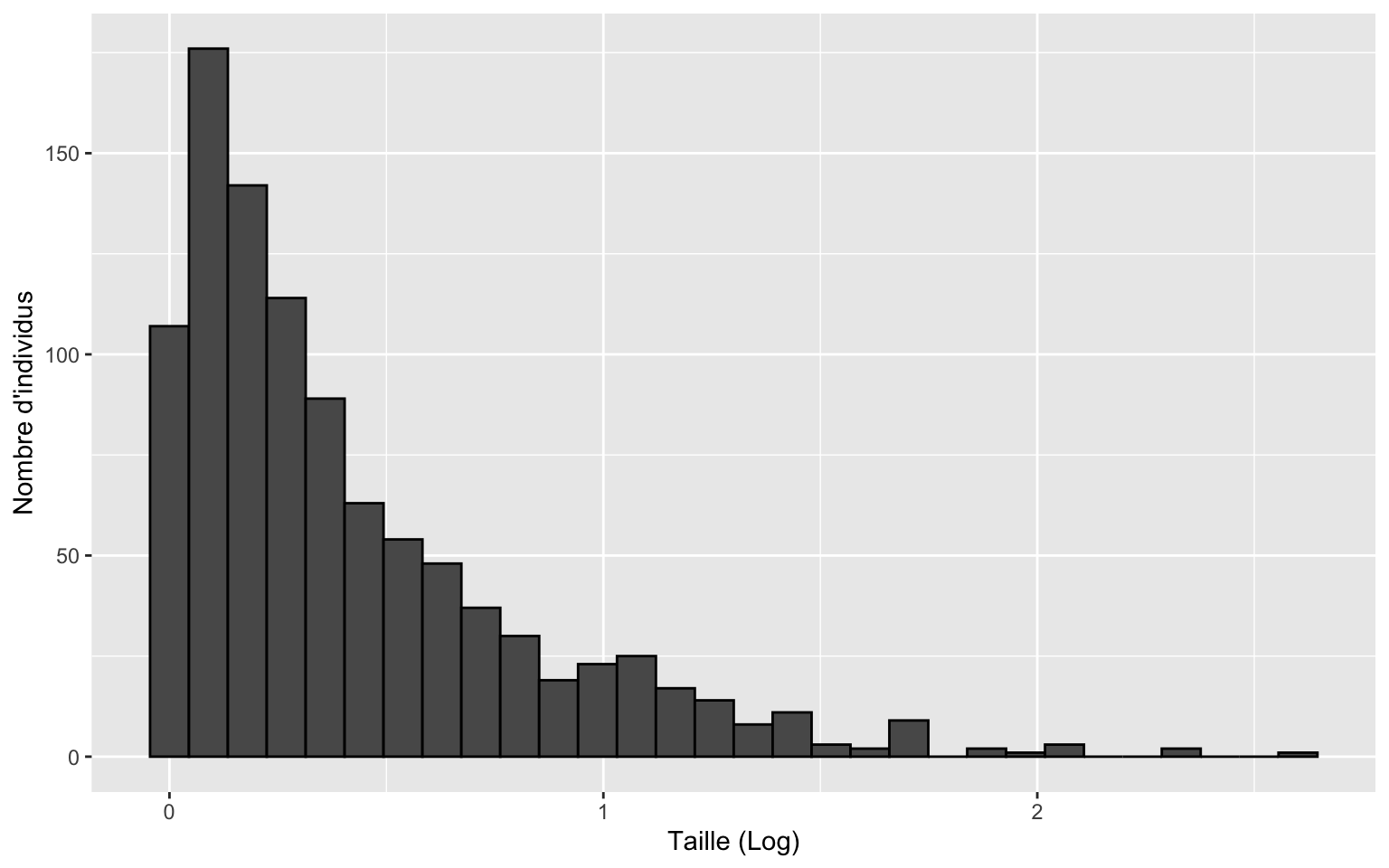
La transformation permet de mieux étaler les petites valeurs de tailles et la structure de nos données est plus visible.

Pour mieux gérer le fait qu’il y a beaucoup plus de petits individus que de gros, on peut aussi utiliser des largeurs de classes variables tout en laissant les tailles en valeurs non-transformées. On peut ainsi augmenter la largeur de classes par un facteur de 2 pour que chaque nouvelle classe soit deux fois plus large que la précédente.

Cela signifie que pour les gros individus, les classes seront très larges, ce qui permettra de capturer davantage d’individus dans chacune d’elles.

bin_breaks <- 2^(0:10)       # Création des bornes des classes qui doublent 


ggplot(dat1, aes(x = x)) +
  geom_histogram(breaks = bin_breaks, color="black") + 
  scale_y_log10(labels = function(x) log10(x)) +         #log transformation des y
  coord_cartesian(xlim = c(0, 300)) +
  labs(x = "Taille (x)", y = "Abondance (log)")

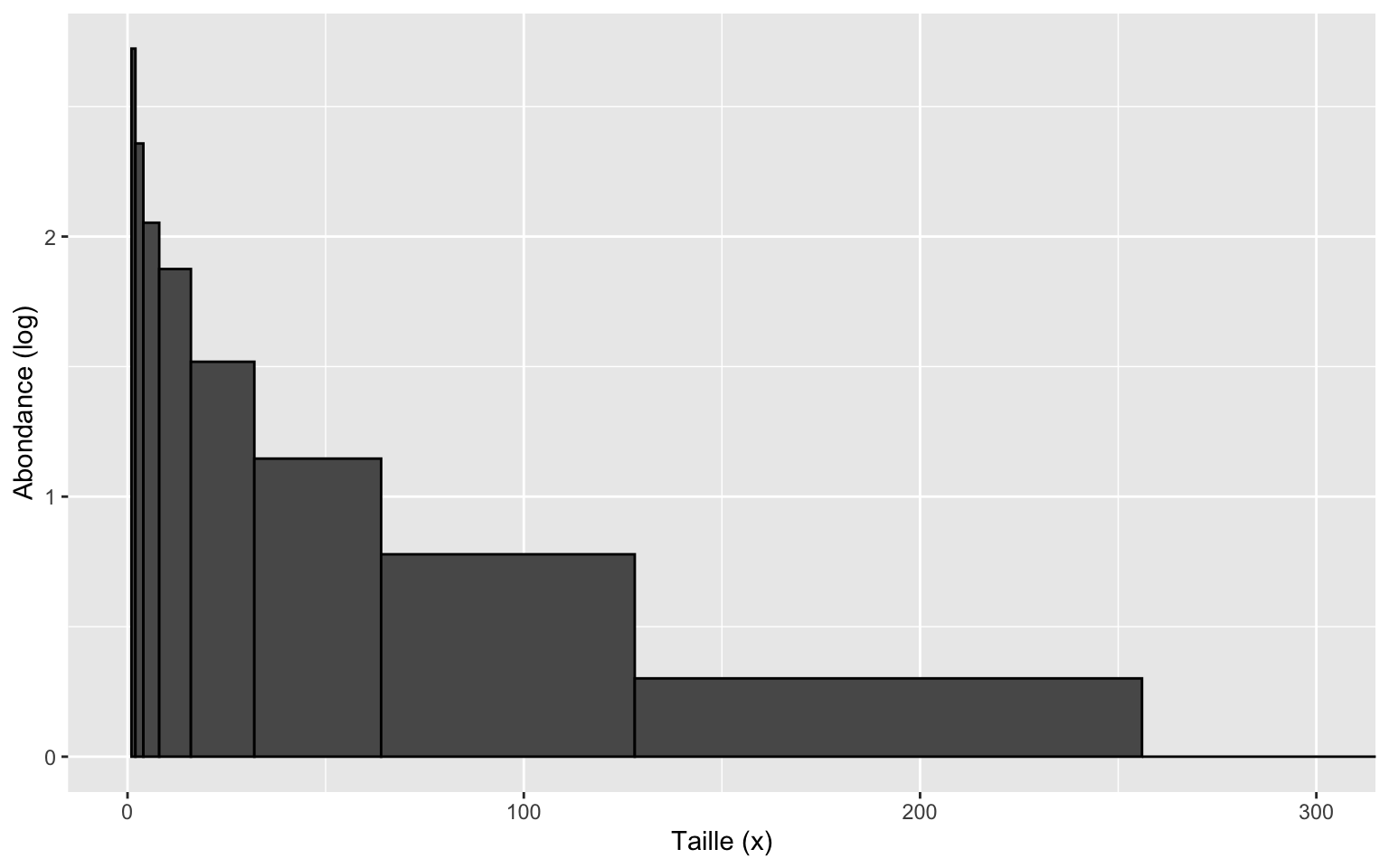
Nous allons voir plus tard que certaines méthodes utilisent cette stratégie pour compenser la rareté naturelle des gros organismes. En élargissant les classes, on évite d’obtenir des zéros (des classes vides) et on accumule assez d’individus pour rendre l’analyse statistique possible.

Cependant, la relation obtenue forme une courbe et il est plus simple d’obtenir une pente à partir d’une relation linéaire. On peut donc log-transformer les valeurs de x et de y:

p <-ggplot(dat1, aes(x = x)) +
  geom_histogram(color="black") + 
  scale_y_log10(labels = function(x) log10(x)) + 
  scale_x_log10(labels = function(x) log10(x)) + 
  
  labs(
       x = "Taille (log)", 
       y = "Nombre d'individus (log)")
p

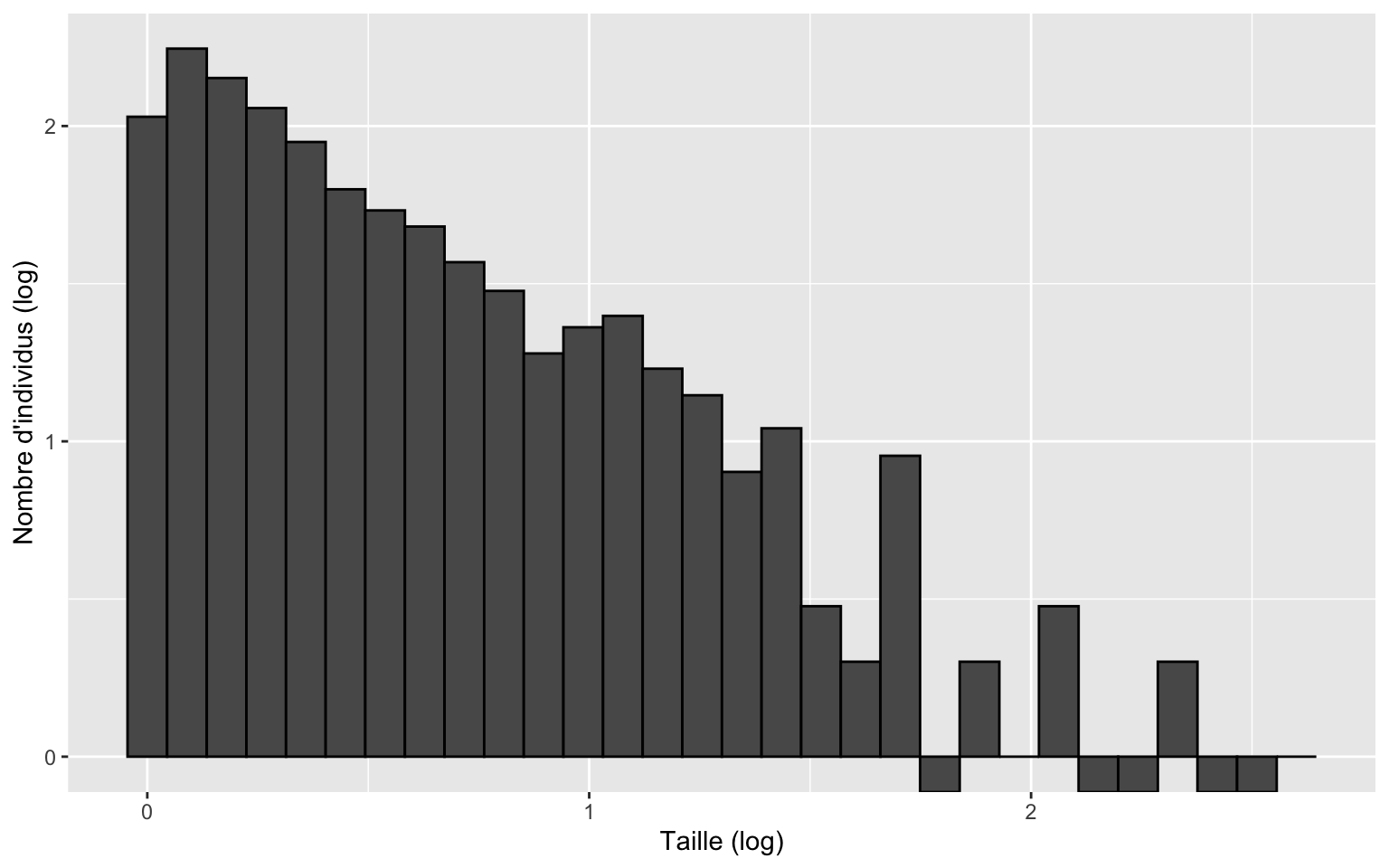
Grâce à la transformation log des deux variables, la relation entre l’abondance et la taille a désormais une apparence linéaire. C’est le point de départ de l’analyse des spectres de tailles. Il devient possible de créer un modèle linéaire et la pente de ce modèle peut servir de métrique standardisée pour comparer différentes communautés en termes de composition des tailles.

Faisons simplement l’exercice d’extraire les points représentés par les barres de l’histogramme ci-dessus (nombre d’individus (log) ~ valeur de x minimale de chaque barre.)

# --- 1. Récupération des données du graphique ---
# On utilise la fonction 'layer_data' pour extraire les valeurs numériques
donnees_graphique <- layer_data(p)

# Nettoyage : On ne garde que les classes qui contiennent des poissons
# (car on ne peut pas faire le log de zéro)
donnees_filtrées <- donnees_graphique[donnees_graphique$count > 0, ]

# --- 2. Calcul de la pente (Régression Linéaire) ---
#y et x min sont log transformées dans les données du graphiques
modele_lineaire <- lm(y ~ xmin, data = donnees_filtrées)


# On reprend l'histogramme de base 'p' et on ajoute la régression linéaire:
p + 
  # 2. La Droite de Régression (Le modèle)
  # geom_abline permet de tracer une ligne avec notre pente et notre point de départ
  geom_abline(intercept = coef(modele_lineaire)[1], 
              slope = coef(modele_lineaire)[2], 
              color = "red", linewidth = 1.2) +
  
  # 3. Mise à jour des titres pour l'explication
  labs(
       x = "Taille (Log)", 
       y = "Abondance (Log)")


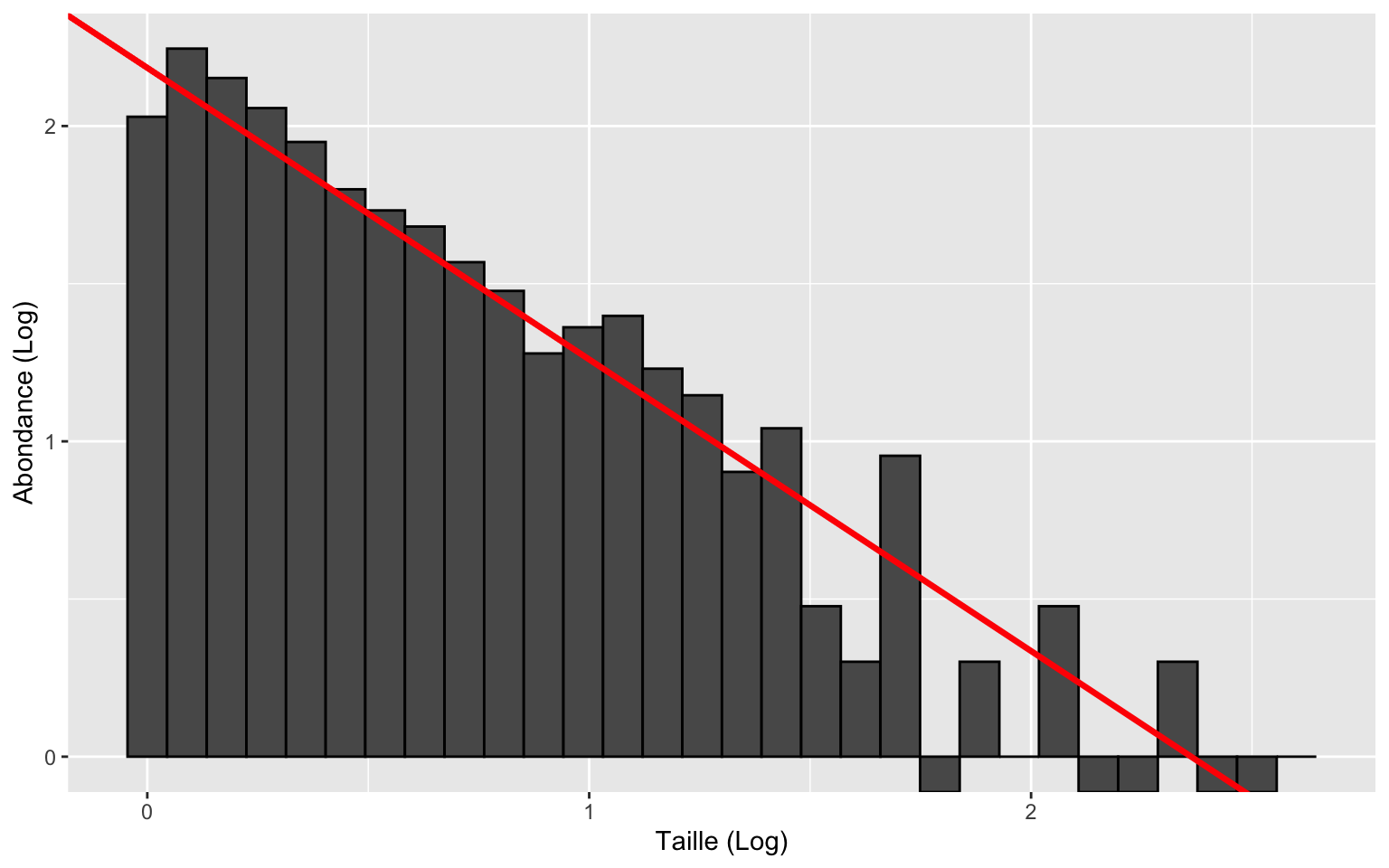
# Extraction du coefficient de la pente
coef(modele_lineaire)[2]

      xmin 
-0.9249218

Ce que nous venons d’effectuer est essentiellement l’une des nombreuses méthodes utilisées dans la littérature pour mesurer les spectres de taille.

En effet, ces méthodes consistent souvent à diviser la communauté en classes de taille et effectuer une régression linéaire. Les différences entre les méthodes résident dans des variations techniques

Observons maintenant la valeur de pente obtenue avec notre méthode. Si la théorie prédit que notre écosystème possède une vraie pente ($b$) de -2, pourquoi notre modèle calcule-t-il une pente de -0.925 ? les transformations effectuées font en sorte que les classes de tailles plus larges capturent artificiellement plus d’individus, ce qui modifie la droite et la rend moins abrupte.

Pour prendre en considération ce biais, la correction standard est: pente réelle ($b$)= pente calculée - 1 (Edwards et al., 2017) . Si nous appliquons cette correction, $b$=-0.925-1= -1.925. Nous retrouvons une valeur très près de la valeur réelle.

BLOC B: Méthodes d’estimation de la pente et leur qualité

Maintenant que nous avons généré une communauté théorique dont nous connaissons la structure (pente de -2), nous pouvons tester notre capacité à retrouver cette valeur. Cette section de l’atelier repose sur l’étude de référence menée par Edwards et al. (2017) publiée dans Methods in Ecology and Evolution. Dans cet article, les auteurs ont recensé et analysé les 8 méthodes historiquement utilisées par les chercheur.es pour estimer la pente des spectres de tailles.

Dans une démarche de reproductibilité, nous allons utiliser le package R sizeSpectra, développé par ces mêmes auteurs, pour appliquer systématiquement ces 8 méthodes à nos données simulées.

eight.results = eightMethodsMEE(x, num.bins = 8) # Uniquement besoin d'intégrer notre vecteur de données "x" et de préciser le nombre de classes de tailles que l'on veut.

Créons la figure où chaque panneau correspond à l’une des méthodes.

eight.methods.plot(eight.results)

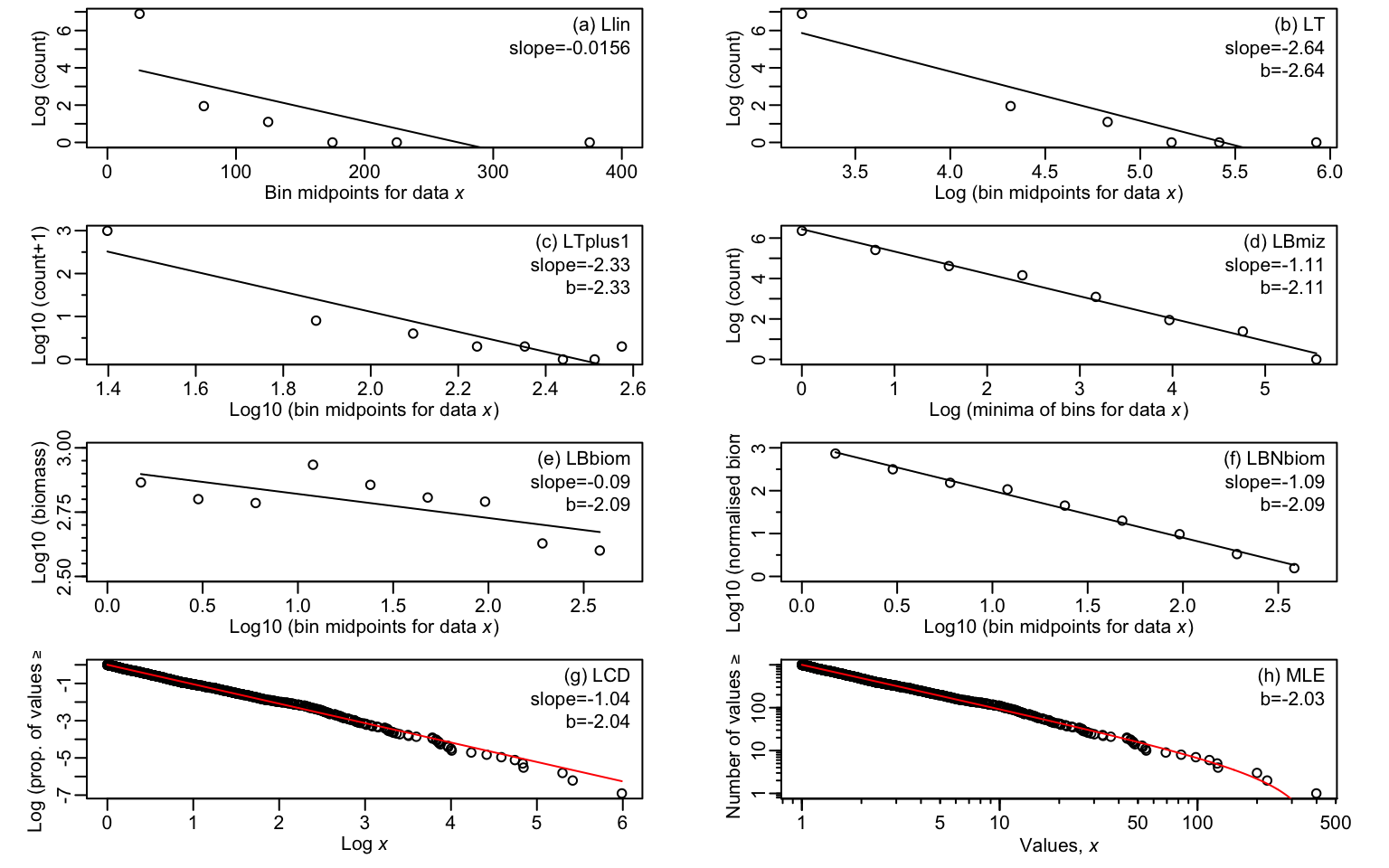
Voici une liste qui résume chacune des méthodes présentes dans la figure:

A) Llin (log-linéaire):

On regroupe les données dans des classes de largeur constante (ex: 0-10g, 10-20g, etc.). On effectue ensuite une régression linéaire de l’abondance (transformée en log) en fonction du point milieu de la classe (échelle linéaire).

En gardant l’axe X linéaire, cette méthode force mathématiquement une relation exponentielle ($y = a \cdot e^{bx}$). Par conséquent, la pente calculée ne peut pas être reliée à l’exposant $b$.

B) LT (log-transformation)

On conserve le même découpage que la méthode A (classes de largeur arithmétique constante). Cette fois, on transforme les deux axes: on effectue une régression linéaire du logde l’abondance en fonction du log du point milieu de la classe.

C) Lt+1 (log-transformation+1)

Comme Lt, mais on ajoute +1 pour ne pas perdre les classes vides, car log(0) est impossible). On effectue ensuite une régression linéaire.

Ainsi, chacune des 8 classes de tailles sont incluent dans la régression linéaire contrairement aux méthodes Llin et LT.

D) LBmiz

Cette méthode se distingue par l’utilisation de classes dont la largeur augmente exponentiellement. De plus, la plus grande classe est fixée à la même largeur arithmétique que l’avant-dernière.

Puisque les classes s’élargissent, elles capturent artificiellement plus d’individus vers la fin. La pente obtenue estime donc $b + 1$ (il faut soustraire 1 pour avoir le vrai $b$)

E) LBiom

On utilise le point milieu de chaque classe de tailles qui augmentent exponentiellement en X. En Y, chaque point correspond à la somme totale de la biomasse contenue dans la classe. Le décalage de +2 est la somme de deux distorsions mathématiques : le premier +1 vient du fait qu’on somme la masse (au lieu de compter les individus), et le deuxième +1 vient du fait que les classes s’élargissent et capturent artificiellement de plus en plus de biomasse.

F) LBNbiom

Il s’agit de la LBiom avec une seule variation. La différence majeure est la normalisation : sur l’axe Y, on divise la biomasse totale de chaque classe par la largeur de cette classe. Cette division annule le biais dû à l’élargissement des classes. Par conséquent, la pente du graphique estime $b + 1$ (seul l’effet de la biomasse subsiste).

G) LCD

Cette méthode évite le regroupement en classes et utilise les tailles individuelles triées par ordre décroissant (le plus grand = rang 1). On effectue une régression du logarithme de la fréquence cumulée (rang/$n$), soit la proportion d’individus de taille supérieure ou égale à $x$, en fonction du logarithme de la taille ($x$). Le résultat de la pente est approximativement $b + 1$.

H) MLE

Cette méthode repose sur l’estimation par le maximum de vraisemblance (MLE). Contrairement aux autres approches, elle ne nécessite aucun regroupement préalable ni construction graphique pour obtenir la valeur de la pente. Elle calcule directement la valeur la plus probable du paramètre $b$. Les résultats peuvent ensuite être illustrés sur un graphique de type rang/fréquence.

Quelle méthode devrait-on prioriser dans une étude?

Globalement, les pentes diffèrent fortement selon les méthodes, allant de −2,64 à −0,02. Toutefois, ces pentes ne peuvent pas être comparées directement, car l’estimation du paramètre ne repose pas sur les mêmes quantités. Il devient donc pertinent d’évaluer la performance de chacune des méthodes dans l’optique de sélectionner une approche standard.

Pour évaluer réellement la fiabilité des 8 méthodes, il est nécessaire de répéter l’expérience un grand nombre de fois. Dans leur étude, Edwards et al. (2017) ont réalisé cette validation exhaustive en générant 10 000 jeux de données simulés indépendants.

Chaque jeu de données respecte les mêmes paramètres que notre exemple précédent :

La figure ci-dessous présente la distribution des pentes estimées par chaque méthode pour ces 10 000 simulations.

Note technique : Puisque la simulation et l’ajustement de 10 000 jeux de données demandent un temps de calcul considérable, les auteurs ont inclus les résultats pré-calculés directement dans le package sizeSpectra (sous l’objet eight.results.default).

Nous allons donc charger ces résultats pour gagner du temps et afficher les histogrammes.

list2env(eight.results.default, envir=.GlobalEnv)    # Extraction des résultats pré-calculés

<environment: R_GlobalEnv>

#> <environment: R_GlobalEnv>


#---Afficher les résultats sous forme d'histogrammes---

xrange = c(-3.5, 0.5)                             # range de l'axe des x
xbigticks = seq(-3.5, 0.5, 0.5)                   # Déterminer où sont les gros traits sur l'axe des x (de −3.5 à 0.5, avec un pas de 0.5)
xsmallticks = seq(xrange[1], xrange[2], by=0.1)   # Déterminer où sont les petites traits sur l'axe des x

breakshist = seq(xrange[1], xrange[2], by=3/61)    # définit la largeur exacte des barres d'histogramme 
# (3/61 pour que le trait de -2 tombe directement au milieu d'une barre et non à cheval entre 2)

# marges
par(omi = c(0.12, 0.05, 0.12, 0.0))   # ajustement des marges extérieures pour que tout rentre dans la figure globale
par(mfrow=c(4,2)) # diviser la fenêtre graphique en 4x2
oldmai = par("mai")             # sauvegarde de sécurité des marges
# par : paramètres graphiques
par(mai=c(0.5, 0.5, 0.1, 0.3)) # déterminer l'espace blanc autour de chaque graphique
par(xaxs="i", yaxs="i")    # Pour que les axes touchent aux histogrammes.
par(mgp=c(2.0, 0.5, 0))    # Mets les labels d'axes plus près 
par(cex = 0.8)             # réduire le texte à 80% de sa taille normale

# axe verical à -2
vertCol = "red"            # couleur de l'axe vertical de la valeur de b réelle
vertThick = 1              # épaisseur axes verticales

xLim = c(-3.2, -1.5)       #limites de l'axe x des graphiques
xLimLlin = xLim + 2        # on met une limite spéciale pour la méthode Llin fixée à nos xlim+2
ylimA = c(0, 5500)         # limites de l'axe des y des graphiques
ylimLlin = c(0, 10000)     # limites de l'axe des y du graphique Llin
cexAxis = 0.9              # contrôler la taille des chiffres sur les axes (90% de la taille normale)

#HISTOGRAMMES

# Histogramme de Llin
hist(Llin.rep.df$slope, xlim=xLimLlin, breaks=breakshist - breakshist[31],
  xlab="", ylab="Frequency",
  main="", axes=FALSE, ylim = ylimLlin)  
axis(1, at=xbigticks, labels = xbigticks, mgp=c(1.7,0.7,0), cex.axis=cexAxis) # graduations majeures sur l'axe des x.
axis(1, at=xsmallticks, labels=rep("",length(xsmallticks)), tcl=-0.2) # graduations mineures sur l'axe des x.
axis(2, at=c(0, 5000, 10000),   # Graduations majeures sur l'axe des y.
         labels = c(0, 5000, 10000),
         mgp=c(1.7,0.7,0), cex.axis=cexAxis)  
axis(2, at=seq(0, 10000, 1000),  # Graduations mineures sur l'axe des y.
         labels = rep("", 11),
         mgp=c(1.7,0.7,0))  

abline(v=b.known, col=vertCol, lwd=vertThick) # ligne rouge de la valeur réelle
inset = c(-0.08, -0.08)     # léger ajustement de la position de la légende
legend("topleft", "(a) Llin", bty="n", inset=inset) # ajoute l'étiquette "(a) Llin" en haut à gauche.

figlabpos = 0.93     # définir variable pour placer le texte à 93% de la hauteur disponible
xlabpos = 0.75       # définir variable pour placer le texte à 0.75% de l'axe horizontal
text( xlabpos, figlabpos * 1100, "(a) Llin", pos=4) #affichage de l'étiquette "(a) Llin" 


# Histogramme de LT
hist(LT.rep.df$slope, xlim=xLim, breaks=breakshist, xlab="", ylab="Frequency",
  main="", axes=FALSE, ylim = ylimA)  
histAxes()
legend("topleft", "(b) LT", bty="n", inset=inset) # ajoute l'étiquette "(b) LT" en haut à gauche.

# Histogramme de LTplus1
hist(LTplus1.rep.df$slope, xlim=xLim, breaks=breakshist, xlab="", ylab="Frequency",
  main="", axes=FALSE, ylim = ylimA) 
histAxes()
legend("topleft", "(c) LTplus1", bty="n", inset=inset) # ajoute l'étiquette "(c) LTplus1" en haut à gauche.

# Histogramme de LBmiz
hist(LBmiz.rep.df$slope - 1, xlim=xLim, breaks=breakshist, xlab="", ylab="Frequency",
  main="", axes=FALSE, ylim = ylimA) 
histAxes()
legend("topleft", "(d) LBmiz", bty="n", inset=inset) # ajoute l'étiquette "(d) LBmiz" en haut à gauche.

# Histogramme de LBbiom
hist(LBbiom.rep.df$slope - 2, xlim=xLim, breaks=breakshist, xlab="", ylab="Frequency",
  main="", axes=FALSE, ylim = ylimA)  
histAxes()
legend("topleft", "(e) LBbiom", bty="n", inset=inset) # ajoute l'étiquette "(e) LBbiom" en haut à gauche.

# Histogramme de LBNbiom
hist(LBNbiom.rep.df$slope - 1, xlim=xLim, breaks=breakshist, xlab="", ylab="Frequency",
  main="", axes=FALSE, ylim = ylimA)  
histAxes()
legend("topleft", "(f) LBNbiom", bty="n", inset=inset) # ajoute l'étiquette "(f) LBNbiom" en haut à gauche.

# Histogramme LCD
hist(LCD.rep.df$slope - 1, xlim=xLim, breaks=breakshist, xlab="", ylab="Frequency",
  main="", axes=FALSE, ylim = ylimA) 
histAxes()
legend("topleft", "(g) LCD", bty="n", inset=inset) # ajoute l'étiquette "(g) LCD" en haut à gauche.

# Histogramme MLE
hist(MLE.rep.df$b, xlim=xLim, breaks=breakshist, xlab="", ylab="Frequency",
  main="", axes=FALSE, ylim = ylimA) 
histAxes()
legend("topleft", "(h) MLE", bty="n", inset=inset) # ajoute l'étiquette "(h) MLE" en haut à gauche.

# Écrire la légende en bas "Estimmé de b" dont b est en italliques.
mtext(expression(paste("Estimé de ", italic(b))), side=1, outer=TRUE, line=-1)

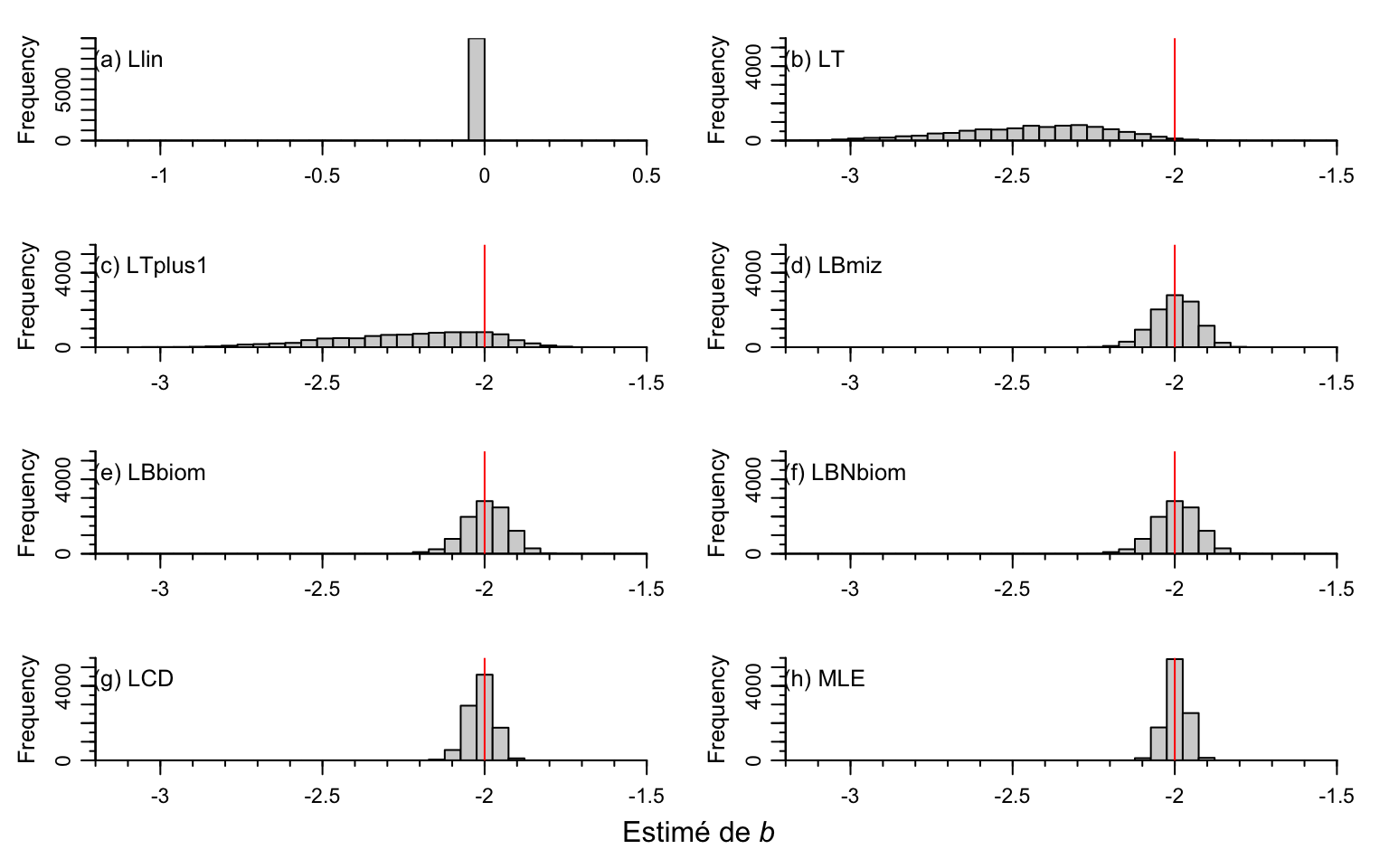
La précision d’une méthode est déterminé par l’allure de l’histogramme par rapport à la valeur réelle. Il doit être centré sur la ligne rouge et être le plus étroit possible.

Ce qu’on observe:

Il est crucial de pouvoir associer une mesure d’incertitude fiable à notre estimation unique de pente.

Pour évaluer la fiabilité de ces mesures, nous allons examiner les intervalles de confiance générés pour nos 10 000 jeux de données simulés (toujours à partir des résultats pré-calculés dans le package sizeSpectra sous l’objet eight.results.default.

La figure suivante présente ces intervalles pour un sous-échantillon de simulations :

par(omi = c(0.14, 0, 0.1, 0.15))      # ajustement des marges extérieures pour que tout rentre dans la figure globale
par(mfrow=c(4,2)) # diviser la fenêtre graphique en 4x2

oldmai = par("mai")           # sauvegarde de sécurité des marges
par(mai=c(0.3, 0.5, 0.08, 0))  # déterminer l'espace blanc autour de chaque graphique
par(xaxs="i", yaxs="i")    # Pour que les axes touchent aux histogrammes.
par(mgp=c(2.0, 0.5, 0))    # Mets les labels d'axes plus près 
par(cex = 0.8)             # réduire le texte à 80% de sa taille normale
vertThick = 1              # épaisseur axes verticales



#----GRAPHIQUES-----

#----Llin-----
Llin.rep.conf.sort = confPlot(Llin.rep.df[ ,-1], legName="(a) Llin",
    xLim = c(-0.25, 0.25)) # parce que les valeur de b ne sont pas près de la réelle

#----LT-----
LT.rep.conf.sort = confPlot(LT.rep.df[ ,-1], legName="(b) LT", yLab="", yLabels=FALSE)

#----LT + 1-----
LTplus1.rep.conf.sort = confPlot(LTplus1.rep.df[ ,-1], legName="(c) LTplus1")

xLimCom = c(-2.65, -1.5)    # Largeur commune de l'axe des x pour LBmiz, LBbiom, LBNbiom, LCD et MLE

#----LBmiz-----
LBmiz.rep.conf.sort = confPlot(LBmiz.rep.df[ ,-1] - 1, legName="(d) LBmiz", 
# On soustrait 1 à tout l'intervalle. (Car la méthode estime b+1).
    xLim = xLimCom, yLab="", yLabels=FALSE)

#----LBiom----
LBbiom.rep.conf.sort = confPlot(LBbiom.rep.df[ ,-1] - 2, legName="(e) LBbiom",
# On soustrait 2 à tout l'intervalle. (Car la méthode estime b+2).
      xLim = xLimCom)

#----LBNbiom-----
LBNbiom.rep.conf.sort = confPlot(LBNbiom.rep.df[ ,-1] - 1, legName="(f) LBNbiom",
# On soustrait 1 à tout l'intervalle. (Car la méthode estime b+1).
     yLab="", yLabels=FALSE, xLim = xLimCom)

#----LCD-----
LCD.rep.conf.sort = confPlot(LCD.rep.df[ ,-1] - 1, legName="(g) LCD",
# On soustrait 1 à tout l'intervalle. (Car la méthode estime b+1).
    xLim = xLimCom, vertFirst = TRUE)

#----MLE-----
MLE.rep.conf.sort = confPlot(MLE.rep.df[ ,-1], legName="(h) MLE",
    xLim = xLimCom, yLab="", yLabels=FALSE)

mtext(expression(paste("Estimate of ", italic(b)), sep=""), #Titre global sous la figure
      side=1, outer=TRUE, line=-0.2, cex=0.8)

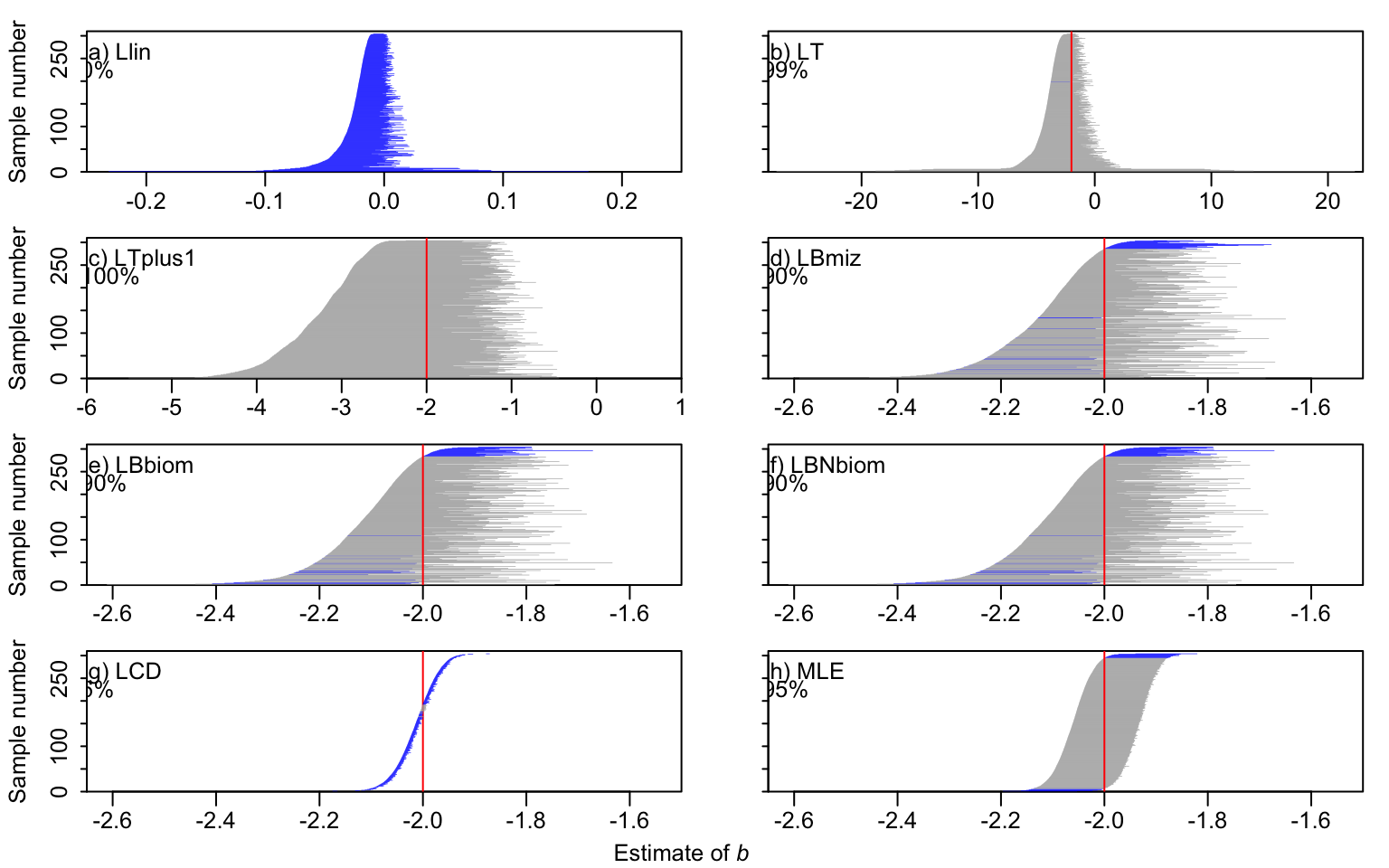
Puisqu’on génère des intervalles de confiance 95%, on devrait théoriquement voir que 95% d’entre elles incluent la vraie valeur. Comme ici la vraie valeur est connue grâce à la simulation, on peut simplement compter combien d’intervalles la contiennent réellement. Cette proportion est la couverture observée.

Les méthodes basées sur la régression linéaire échouent lourdement : Llin rate systématiquement la cible, les méthodes LT et LT+1produisent des intervalles trop larges pour être utiles, et la méthode LCD donne une fausse impression de précision avec des intervalles beaucoup trop étroits (seulement 6 % de succès).

Les méthodes de regroupement par classes (LBmiz, LBbiom, LBNbiom) sont mieux, mais elles n’incluent la vraie valeur que 90 % du temps au lieu des 95 % requis.

Seule la méthode MLE valide les attentes, produisant des intervalles de confiance cohérents qui contiennent la vraie valeur exactement 95 % du temps.

Selon les résultats obtenus. La méthode MLE devrait être privilégiée pour estimer la pente de spectre de tailles lorsque les données disponibles le permettent.

BLOC C: Méthode MLE

Puisque MLE est la seule méthode qui offre une estimation non-biaisée et une précision statistique optimale pour les spectres de tailles, voici le code nécessaire pour appliquer cette méthode lorsqu’on possède un vecteur de données de tailles d’organismes. Prenons notre vecteur intial “x” de 1000 observations.

#################################### Fonction pour calculer la pente du spectre de taille (et intervalles de confiance) d'un vecteur x de tailles avec la méthode MLE 
MLE.method <- function(x){                # x : Le vecteur de données (tailles des organismes) 
  xmin = min(x)                           # trouver l'organisme le plus petit
  xmax = max(x)                           # trouver l'organisme le plus gros
  log.x = log(x)
  sum.log.x = sum( log.x )
  
 
  PL.bMLE = 1/( log(min(x)) - sum.log.x/length(x)) - 1 # Formule simplifiée (loi non-bornée) pour donner une piste à l'algorithme
  PLB.minLL =  nlm(negLL.PLB,             # negLL.PLB est la fonction (package sizeSpectra) à maximiser
                   p=PL.bMLE,             # Point de départ
                   x=x,                   
                   n=length(x), 
                   xmin=xmin,
                   xmax=xmax,
                   sumlogx=sum.log.x) 
  
  PLB.bMLE = PLB.minLL$estimate           # On extrait la meilleure pente trouvée (le résultat)
  
  #intervalles de confiance 95%
  PLB.minNegLL = PLB.minLL$minimum
  bvec = seq(PLB.bMLE - 0.5, PLB.bMLE + 0.5, 1e-05) # On crée une zone de recherche autour de la valeur de pente esitmée (100 000 points testés)
  PLB.LLvals = vector(length = length(bvec)) 
  for (i in 1:length(bvec)) {
    PLB.LLvals[i] = negLL.PLB(bvec[i], x = x, n = length(x), 
                              xmin = xmin, xmax = xmax, sumlogx = sum.log.x)
  }                                          # Boucle : On teste le score de probabilité pour chaque pente voisine
  critVal = PLB.minNegLL + qchisq(0.95, 1)/2 # définition d'un seuil
  bIn95 = bvec[PLB.LLvals < critVal]         # On garde toutes les pentes qui sont au-dessus du seuil critique
  PLB.MLE.bConf = c(min(bIn95), max(bIn95))  # Les bornes sont la plus petite et la plus grande valeur ayant réussi le test
  hMLE.list = list(b = PLB.bMLE, confVals = PLB.MLE.bConf) # Regrouper la pente et les intervalles dans une liste unique
  return(hMLE.list = hMLE.list) # Renvoyer le résultat final à l'utilisateur (sortie de la fonction)
}
############################################# FIN DE LA FONCTION MLE.method() 

mle_SPECTRA <- MLE.method(x)  # mettre son vecteur de données dans l'argument

mle_SPECTRA

$b
[1] -2.029697

$confVals
[1] -2.097417 -1.964317

Il vous suffit maintenant d’insérer vos données de tailles dans l’argument “MLE.method()”, et vous pourrez obtenir la pente de spectre de tailles obtenue ainsi qu’un intervalle de confiance.

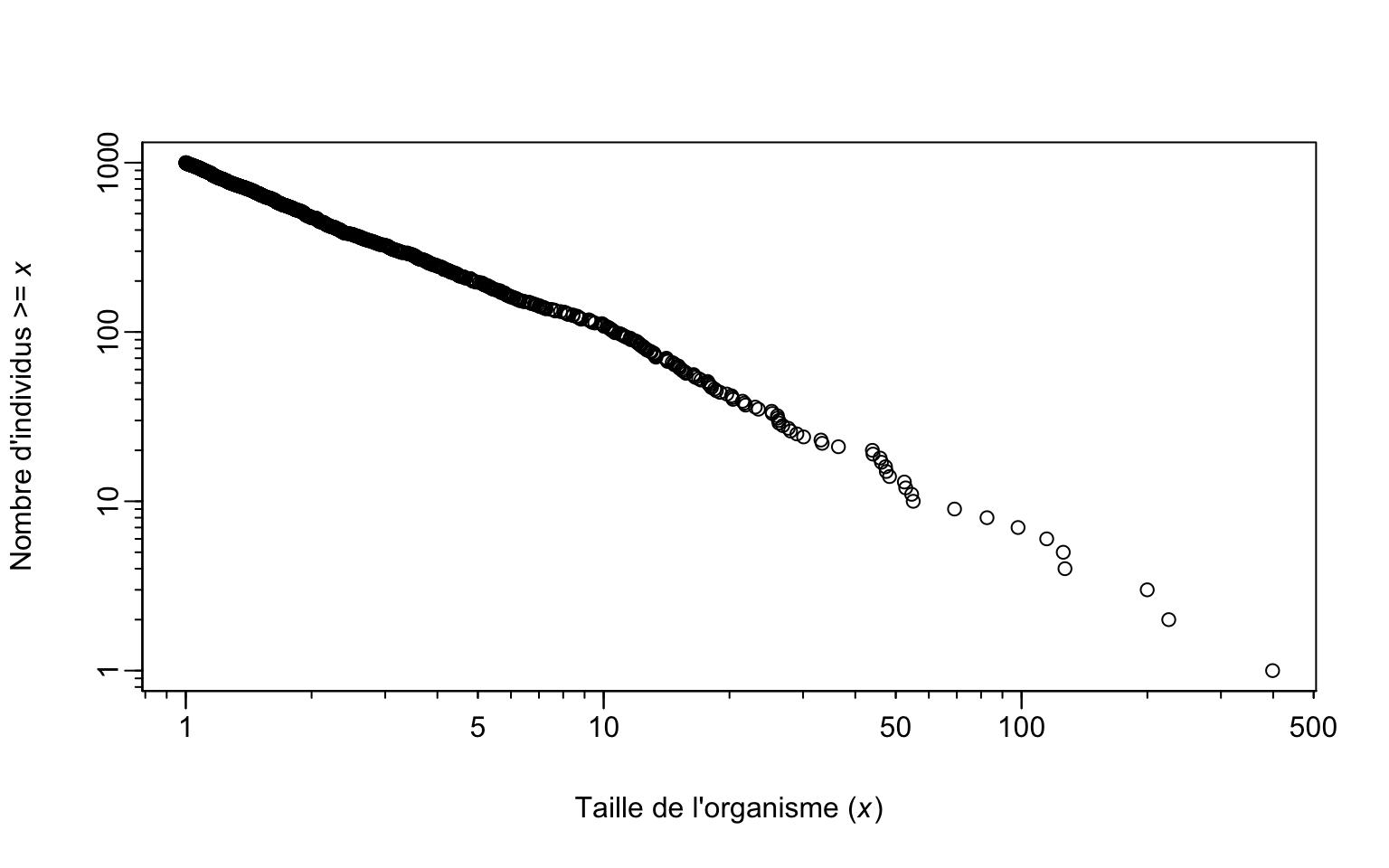
Voici également le code nécessaire pour effectuer une représentation graphique de type rang/fréquence pour un cadre de présentation.

################################################################################
# FONCTION : Visualisation simple du Spectre de Taille 
################################################################################

MLE.plot <- function(x, 
                            log.xy = "xy",            # axes X et Y en log
                            xlim_global = NA,         # Limites manuelles (optionnel)
                            ylim_global = NA         # Limites manuelles (optionnel)
                              
                                               
)
{
  # --- 1. Définition des limites du graphique ---
  
  # Si aucune limite X n'est fournie, on prend le min et le max des données
  if(is.na(xlim_global[1])){
    xlim_global = c(min(x), max(x))
  }
  
  # Si aucune limite Y n'est fournie, on va de 1 (le plus gros) à N (le total)
  if(is.na(ylim_global[1])){
    ylim_global = c(1, length(x))
  }
  
  # --- 2. Création du graphique ---
  
  plot(
    # A. L'axe X (Les tailles) : 
    # On trie les données de la plus grande à la plus petite (decreasing = TRUE).
    sort(x, decreasing = TRUE),
    
    # B. L'axe Y (Les rangs/Fréquence cumulée) :
    # On crée une suite de 1 jusqu'au nombre total d'individus.
    # Le 1er point (le plus gros) a le rang 1. Le dernier (le plus petit) a le rang N.
    1:length(x),
    
    # C. Les échelles :
    # "xy" signifie que les deux axes sont transformés en log.
    log = log.xy,
    
    # D. Les étiquettes (Labels) :
    xlab = expression(paste("Taille de l'organisme (", italic(x), ")")),
    ylab = expression(paste("Nombre d'individus >= ", italic(x))),
    
    # E. Gestion des axes :
    # axes = FALSE signifie "Ne dessine pas les axes par défaut".
    # On veut utiliser nos propres axes
    xlim = xlim_global,
    ylim = ylim_global,
    axes = FALSE
  )
  
  # --- 3. Dessin des axes (Optionnel mais esthétique) ---
  # Elle sert à mettre des graduations (1, 10, 100) lisibles sur une échelle log.
  
  # On récupère les coordonnées exactes du graphique actuel
  xLim = 10^par("usr")[1:2] 
  yLim = 10^par("usr")[3:4]
  
  # Si on est en Log-Log ("xy"), on dessine les graduations sur les deux axes
  if(log.xy == "xy"){
    # logTicks est une fonction utilitaire
    logTicks(xLim, yLim, xLabelSmall = c(5, 50, 500)) 
  }
  
  # Si on est seulement en Log X ("x"), on adapte les axes 
  if(log.xy == "x"){
     axis(1) # Axe X standard
     axis(2) # Axe Y standard
  }
  
} 
############################################# FIN DE LA FONCTION

MLE.plot(x)

BLOC D: Biais d’échantillonnage

ll peut arriver qu’on a des méthodes d’échantillonnage qui sous-estiment certaines classes de tailles. Par exemple, les mailles d’un filet laissent passer les plus petits poissons. Que faire? On peut effectuer une simulation pour voir comment l’estimation de $b$ change en fonction de si on décide d’inclure les classes de tailles sous-estimées vs lorsqu’on retire ces classes de tailles.

Créons d’abord un nouveau jeu de données théoriques.

set.seed(2112)                                 # Pour la reproductibilité
x <- rPLB(5000, b = -2, xmin = 0.1, xmax = 75) # Création du vecteur de tailles qui génère des données simulées suivant une loi de puissance.

dat1 <- data.frame(x = sort(x))                # Création d'un dataframe qui trie les organismes du plus petit au plus grand.

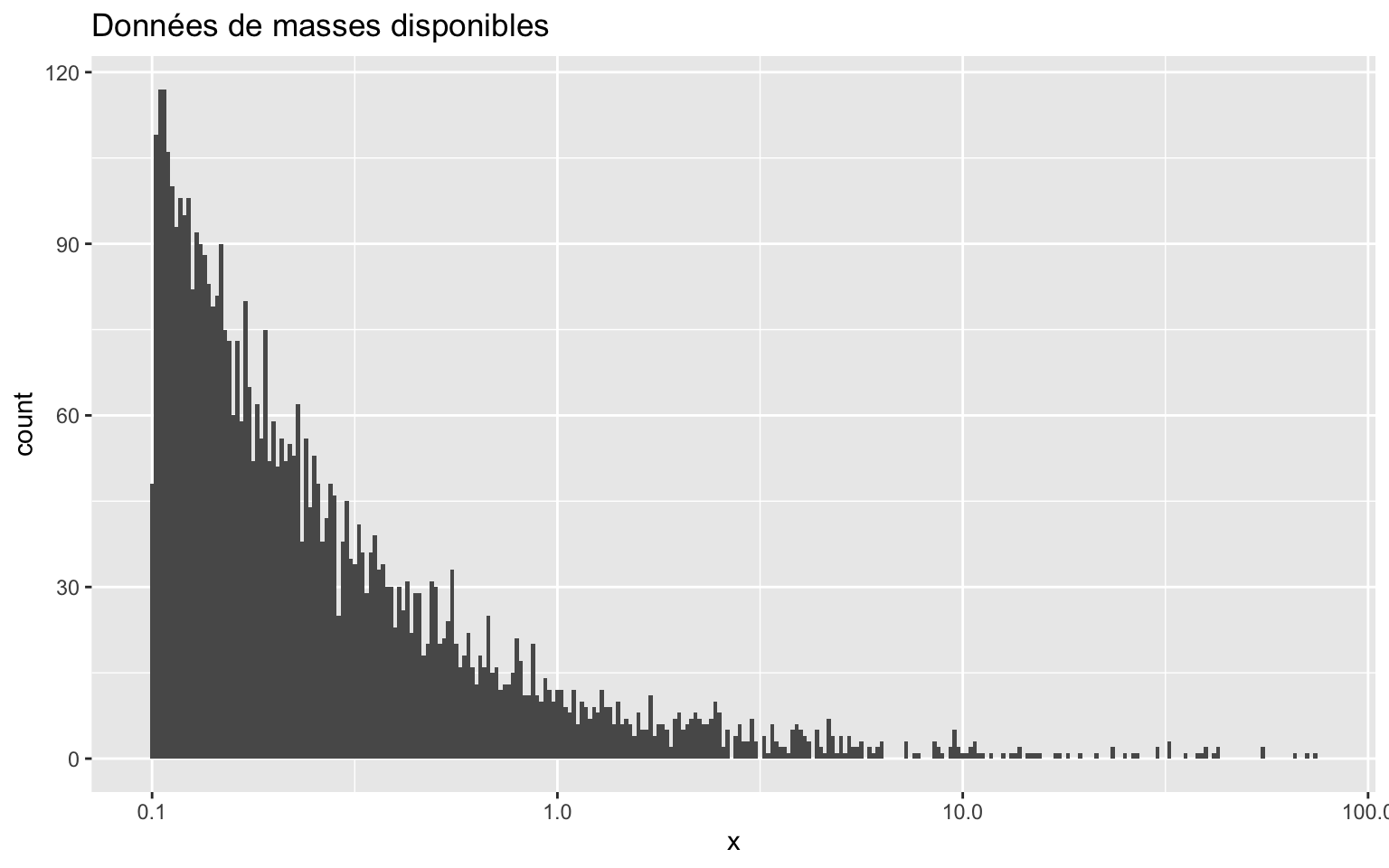
ggplot(dat1, aes(x = x)) +                     # Visualisation des données
  geom_histogram(binwidth = 0.01) +
  scale_x_log10() +
  labs(title = "Données de masses disponibles")


dat1$theta <- 0.5         # Définir le seuil de rétention
dat1 <- dat1 |>
  mutate(pr = case_when(   # Créer une nouvelle colonne 'pr' (Probabilité de capture)
    x < theta ~ 0.01,      # CAS 1 : Si la taille (x) est plus petite que le seuil -> 1% de chance de capture (99% d'échappement)
    .default = 1           # CAS 2 (Défaut) : Pour tout le reste (taille > seuil) -> 100% de chance de capture
  ))
dat1 |>
  group_by(pr) |>          # On regroupe les données selon leur probabilité (0.01 ou 1)
  count()                  # On compte combien d'individus se trouvent dans chaque catégorie (Échappés vs Capturés)

# A tibble: 2 × 2
# Groups:   pr [2]
     pr     n
  <dbl> <int>
1  0.01  4007
2  1      993

Définissons un biais d’échantillonnage. On décide arbitrairement que la limite de performance de l’équipement est 0.5g et que tout ce qui est plus petit a moins de chance d’être capturé.

Selon le tableau, 4007 petits individus subissent le filtre de 1% de chance d’être capturé. 993 gros individus sont échantillonnés.

Capturons maintenant 1000 individus dans cette communauté et observons la distribution des tailles de notre échantillon.

# L'acte de pêche
obs1 <- dat1 |>
  sample_n(size = 1000, weight = pr)   # On capture 1000 individus au total
                                       # Les gros poissons (pr=1) ont 100x plus de chances d'être tirés au sort que les petits (pr=0.01).
# Vérification du contenu du filet
obs1 |>
  group_by(pr) |>                     
  count()                             # On compte combien de "petits difficiles à attraper" vs "gros faciles" on a réellement pêchés.

# A tibble: 2 × 2
# Groups:   pr [2]
     pr     n
  <dbl> <int>
1  0.01    94
2  1      906

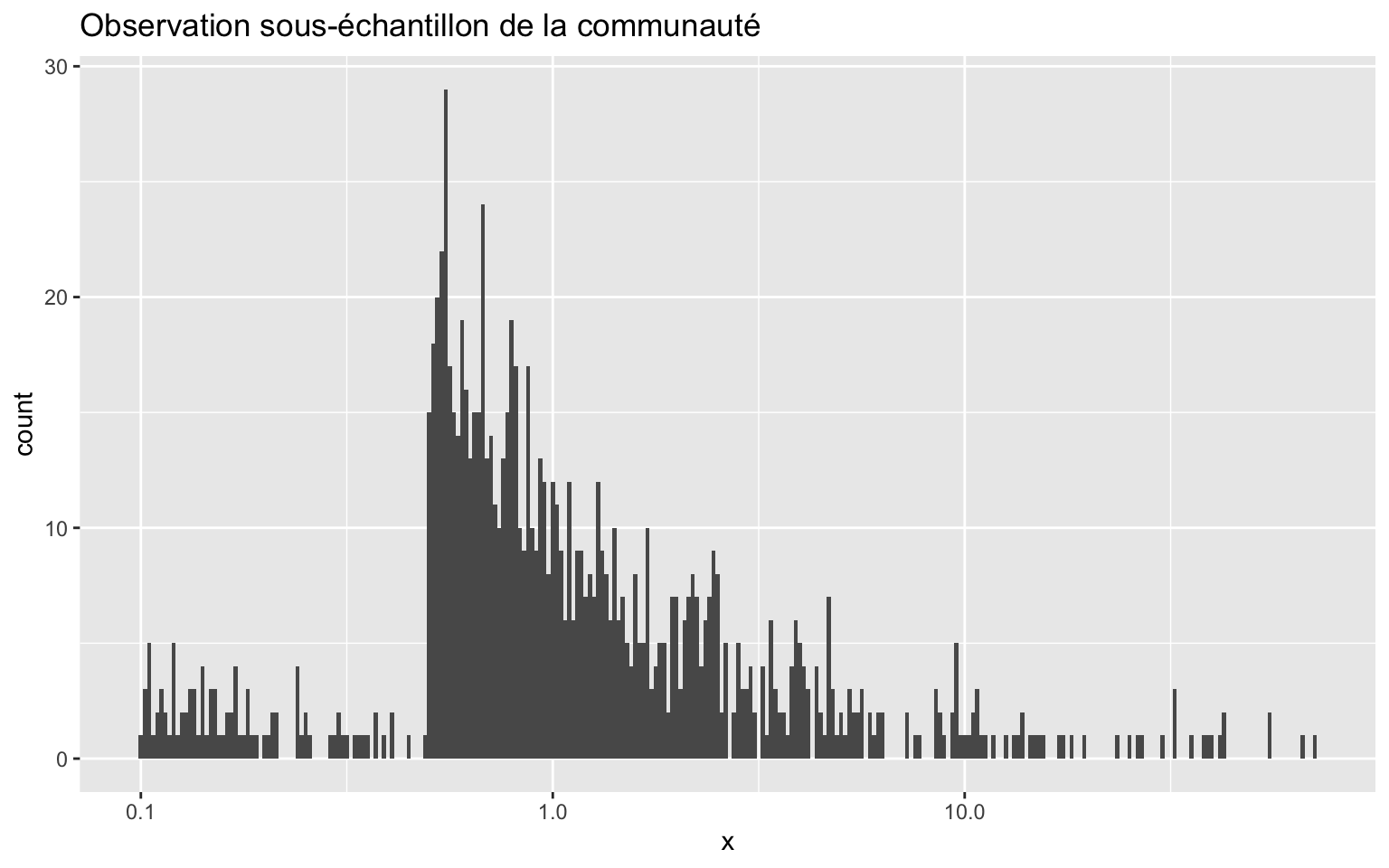
ggplot(obs1, aes(x = x)) +
  geom_histogram(binwidth = 0.01) +
  scale_x_log10() +
  labs(title = "Observation sous-échantillon de la communauté")


mle_test <- MLE.method(obs1$x)
mle_test

$b
[1] -1.261534

$confVals
[1] -1.296924 -1.226574

Si on essaie de calculer une pente $b$ sur toutes les données (y compris la partie biaisée à gauche), on obtient une valeur (-1.26 ) très éloignée de celle de la communauté entière (-2). On surestime la quantité de gros organismes par rapport aux petits.

Une solution serait d’appliquer la MLE sur la partie de l’échantillon qui n’est pas biaisée. Cela revient à identifier un seuil, appelé $x_{min}$, à partir duquel l’engin de capture a fonctionné. Dans certains cas idéaux, cette coupure est évidente à l’œil nu : on voit un “pic” clair suivi d’une descente régulière. On peut donc choisir ce sommet manuellement comme $x_{min}$.

Cependant, dans la réalité, cette coupure est rarement aussi nette. Les données peuvent être contenir du bruit. Choisir $x_{min}$ “à l’œil” devient alors dangereux : deux chercheurs pourraient choisir deux seuils différents et obtenir deux résultats différents.

Pour éviter cette subjectivité, nous utilisons une stratégie automatisée via le package poweRlaw. L’algorithme va tester tous les seuils possibles dans nos données. Pour chaque seuil testé, il compare nos données à une loi de puissance parfaite en effectuant un test de Kolmogorov-Smirnov. Il retiendra automatiquement le $x_{min}$ qui offre le meilleur ajustement statistique entre nos observations et le modèle théorique.

powerlaw = conpl$new(obs1$x)          # Fonction conpl définit que nos données suivent une loi de puissance. Elle                                          précise à "estimate_xmin quelle formule utiliser
xmin1 = estimate_xmin(powerlaw)$xmin  # Fonction estimate_xmin calcule le meilleur x_min
xmin1

[1] 0.4943465

On obtient une valeur minimale de 0.494. Elle correspond presque exactement au seuil de taille qui subit un biais d’échantillonnage. C’est cette valeur qui permet de maximiser la ressemblance de notre distribution à une loi de puissance.

Nous allons donc créer un nouveau jeu de données (trim1) en retirant toutes les observations situées sous le seuil. Nous ne gardons que la “queue” de la distribution qui suit fidèlement la loi de puissance.

obs1$xmin = xmin1         # Ajouter le x min dans notre dataset        
trim1 <- obs1 |>          # On filtre en utilisant la variable calculée (xmin1)
  filter(x > xmin)        # Note : on utilise >= pour inclure la borne

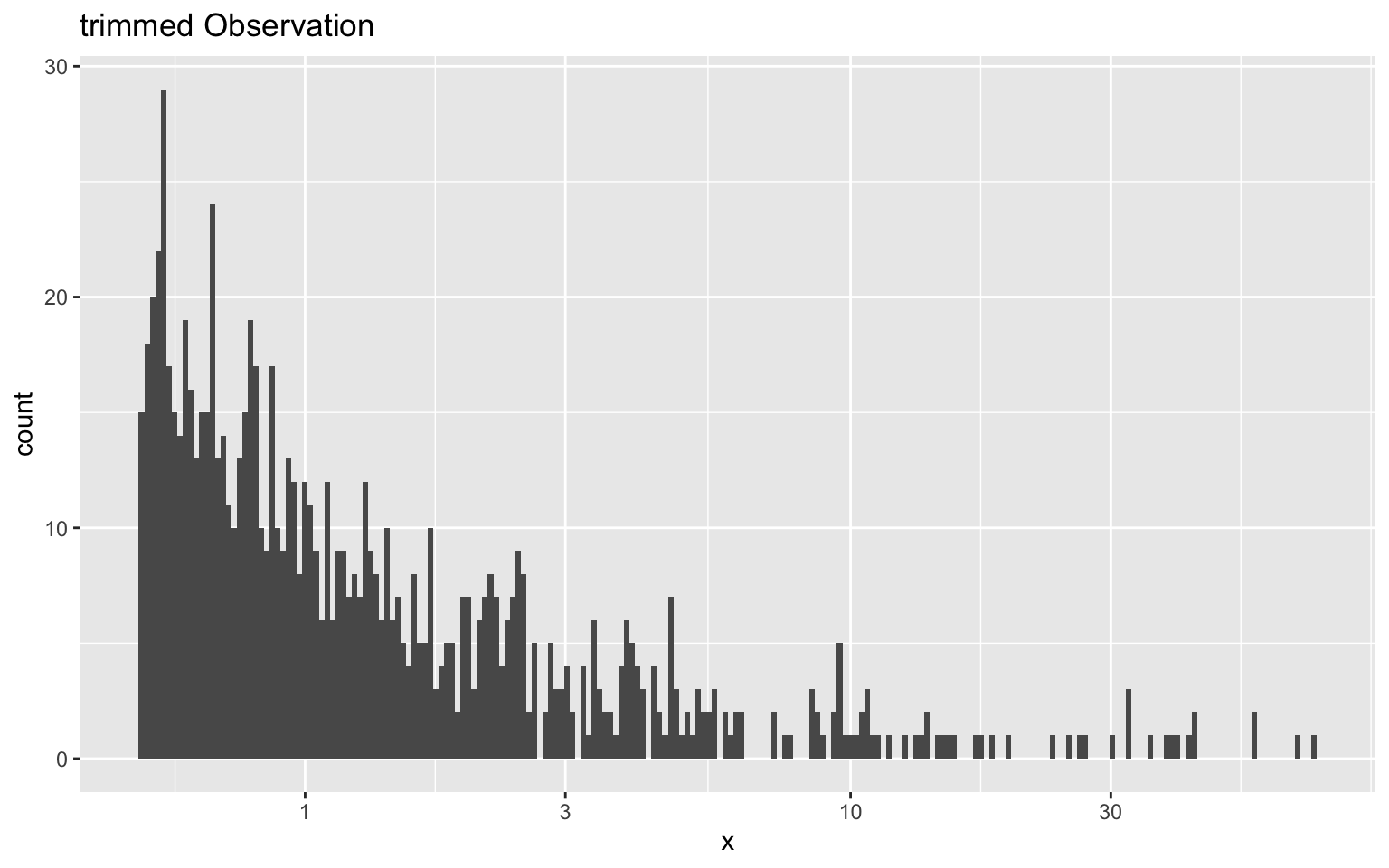
ggplot(trim1, aes(x = x)) +
  geom_histogram(binwidth = 0.01) +
  scale_x_log10() +
  labs(title = "trimmed Observation")

Estimons la pente des données épurées

mle_trim <- MLE.method(trim1$x)
mle_trim

$b
[1] -1.991783

$confVals
[1] -2.064293 -1.921563

La correction nous permet de retrouver la valeur de pente réelle!

Conclusion

À la suite de cet atelier, vous êtes en mesure de mieux saisir la mécanique derrière la création d’un spectre de tailles. Vous possédez désormais le bagage qui vous permet de défendre l’utilisation de la méthode MLE pour effectuer le spectre de tailles d’une communauté dans vos recherches. Vous êtes également équipé pour porter un oeil critique sur les études qui appliquent les différentes méthodes utilisées historiquement. Vous disposez même des outils nécessaires pour faire une analyse de spectre de tailles de qualité en fonction du type de données qui vous sont accessibles.