Algorithme Boruta
Jade Dormoy-Boulanger
Avril 2025
- Étape 1: Vérifications des données
- Étape 2: Le test avec valeur réponse catégorique (utilisation des sols)
- Étape 3: Visualisation des résultats
- Étape 4: Le test avec valeur réponse numérique (zinc)
- Étape 5: Visualisation des résultats
L’algorithme Boruta est basé sur l’apprentissage automatique de sélection de fonctionnalités. En d’autres mots, c’est un algorithme qui permet de sélectionner les variables explicatives significatives (facteurs) d’un modèle donné. Le Boruta est un algorithme “wrapper” utilisant la méthode de classification de “Random Forest” pour entraîner et évaluer un modèle prédictif. Fait amusant: Le nom “Boruta” provient de la mythologie slave où Boruta est un esprit de la forêt.
L’algorithme Boruta est conçu pour fournir une sélection stable et classée par ordre d’importance des facteurs significatifs. Pour ce faire, il compare les scores Z médians des variables d’un modèle avec les scores Z médians de facteurs d’ombre (facteurs basés sur une distribution strictement aléatoire).
Cet algorithme comporte plusieurs caractéristiques intéressantes pour les diverses disciplines relatives à l’environnement:
- Peut être utiliser autant avec des variables catégoriques que continues
- Due à sa nature itérative, il gère très bien la corrélation entre les variables explicatives (donc on n’a pas besoin de s’en soucier!)
- Il classe les facteurs significatifs au modèle par ordre d’importance
- Est très efficace lorsqu’il y a beaucoup de variables explicatives
Boruta comporte également quelques inconvénients:
- Il ne fonctionne pas si le jeu de données comporte des NAs
- Il est relativement lent à exécuter, surtout lorsqu’il y a beaucouyp de données à traiter
NB: Les analyses faites dans ce tutoriels ne font pas de sens scientifiquement parlant, elles sont là à titre d’exemple seulement.
Maintenant qu’on a une idée de ce qu’est le Boruta, c’est le temps de l’essayer!
#Installation et chargement des paquets
#install.packages(c("Boruta", "Amelia", "randomForest", "sp", "pdp"))
library(Boruta)
library(Amelia)
library(randomForest)
library(sp)
library(pdp)
#Données
data("meuse") #jeu de données sur la pollution de métaux lourds dans la plaine d'inondation de La Meuse (Pays-Bas)
Étape 1: Vérifications des données
Il faut vérifier si notre jeu de données comporte des NAs et si les variables catégoriques sont encodées en facteurs.
#Vérification des données
str(meuse) # Tout est beau! Les valeur catégoriques sont encodées en facteurs
'data.frame': 155 obs. of 14 variables:
$ x : num 181072 181025 181165 181298 181307 ...
$ y : num 333611 333558 333537 333484 333330 ...
$ cadmium: num 11.7 8.6 6.5 2.6 2.8 3 3.2 2.8 2.4 1.6 ...
$ copper : num 85 81 68 81 48 61 31 29 37 24 ...
$ lead : num 299 277 199 116 117 137 132 150 133 80 ...
$ zinc : num 1022 1141 640 257 269 ...
$ elev : num 7.91 6.98 7.8 7.66 7.48 ...
$ dist : num 0.00136 0.01222 0.10303 0.19009 0.27709 ...
$ om : num 13.6 14 13 8 8.7 7.8 9.2 9.5 10.6 6.3 ...
$ ffreq : Factor w/ 3 levels "1","2","3": 1 1 1 1 1 1 1 1 1 1 ...
$ soil : Factor w/ 3 levels "1","2","3": 1 1 1 2 2 2 2 1 1 2 ...
$ lime : Factor w/ 2 levels "0","1": 2 2 2 1 1 1 1 1 1 1 ...
$ landuse: Factor w/ 15 levels "Aa","Ab","Ag",..: 4 4 4 11 4 11 4 2 2 15 ...
$ dist.m : num 50 30 150 270 380 470 240 120 240 420 ...
meuse <- meuse[, -c(1,2)] #enlever les coordonnées géographiques, car on n'en a pas besoin pour utiliser le Boruta
#Vérifier les NAs
missmap(meuse) #On a des NAs!
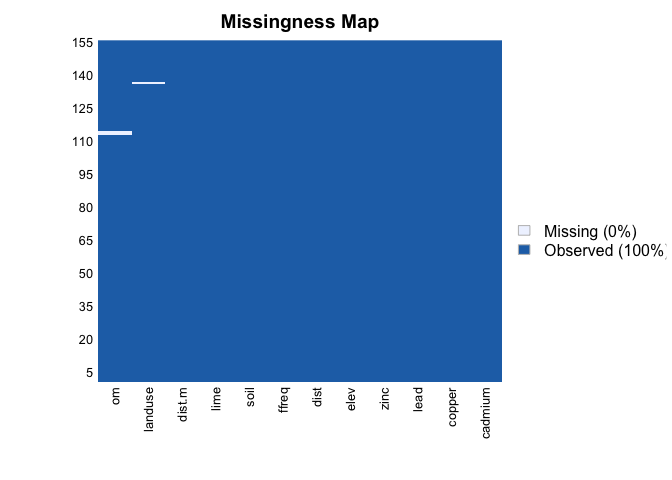
#Enlever les données manquantes
meuse <- na.omit(meuse)# normalement, on aurait générer les données, mais pour l'atelier, c'est parfait
missmap(meuse) #Tout est beau, on continue!
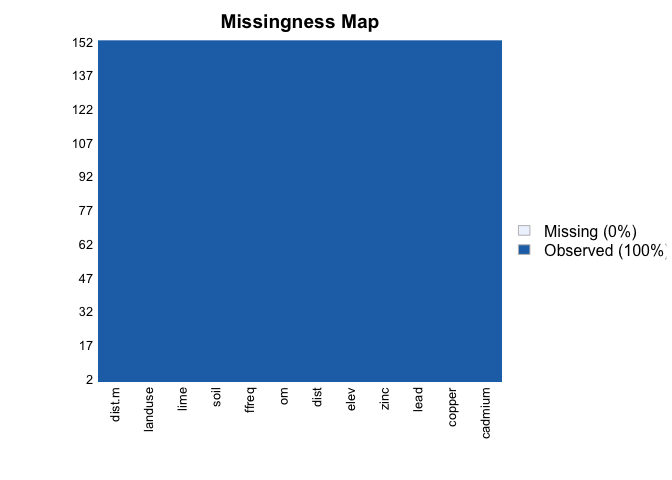
Étape 2: Le test avec valeur réponse catégorique (utilisation des sols)
set.seed(666) # Ajouter de l'aléatoire et assurer la reproductibilité
boruta.tree <- Boruta(landuse~.,meuse, doTrace = 2) # le test
getSelectedAttributes(boruta.tree, withTentative = F) #le résultat
[1] "cadmium" "copper" "lead" "zinc" "elev" "dist" "om"
[8] "soil" "lime" "dist.m"
result.boruta <- attStats(boruta.tree) # sauver les résultats dans un objet
result.boruta # Tout est confirmé sauf ffreq qui est une tentative (fréquence d'inondation)
meanImp medianImp minImp maxImp normHits decision
cadmium 5.945723 6.014663 2.5914729 8.063450 0.9090909 Confirmed
copper 7.113778 7.175817 5.0427523 9.119944 0.9898990 Confirmed
lead 4.376747 4.469601 1.7236572 8.206230 0.8181818 Confirmed
zinc 5.406644 5.400178 2.5531753 7.955784 0.9292929 Confirmed
elev 6.195954 6.224019 2.5389805 9.282901 0.9595960 Confirmed
dist 8.247251 8.232837 5.6687932 10.814695 1.0000000 Confirmed
om 4.900863 4.892887 2.4107399 7.345374 0.8787879 Confirmed
ffreq 3.334017 3.227131 1.1318711 5.830546 0.6161616 Tentative
soil 3.819919 3.889711 2.0409078 7.229944 0.7474747 Confirmed
lime 3.606756 3.697002 0.6825293 5.498580 0.6767677 Confirmed
dist.m 8.362581 8.387298 5.7266492 10.785228 1.0000000 Confirmed
boruta.tree.2 <- TentativeRoughFix(boruta.tree)#classer les tentatives
getSelectedAttributes(boruta.tree.2, withTentative = F)#nouveaux résultats
[1] "cadmium" "copper" "lead" "zinc" "elev" "dist" "om"
[8] "ffreq" "soil" "lime" "dist.m"
result.boruta <- attStats(boruta.tree.2)
result.boruta # Finalement tout est significatif pour expliquer l'utilisation des terres
meanImp medianImp minImp maxImp normHits decision
cadmium 5.945723 6.014663 2.5914729 8.063450 0.9090909 Confirmed
copper 7.113778 7.175817 5.0427523 9.119944 0.9898990 Confirmed
lead 4.376747 4.469601 1.7236572 8.206230 0.8181818 Confirmed
zinc 5.406644 5.400178 2.5531753 7.955784 0.9292929 Confirmed
elev 6.195954 6.224019 2.5389805 9.282901 0.9595960 Confirmed
dist 8.247251 8.232837 5.6687932 10.814695 1.0000000 Confirmed
om 4.900863 4.892887 2.4107399 7.345374 0.8787879 Confirmed
ffreq 3.334017 3.227131 1.1318711 5.830546 0.6161616 Confirmed
soil 3.819919 3.889711 2.0409078 7.229944 0.7474747 Confirmed
lime 3.606756 3.697002 0.6825293 5.498580 0.6767677 Confirmed
dist.m 8.362581 8.387298 5.7266492 10.785228 1.0000000 Confirmed
median<-data.frame(boruta.tree.2$ImpHistory)#données importantes pour rapporter les résultats, normalement, on rapporte les facteurs trouvés significatifs et le taux de réussite de l'algorithme (% de facteurs significatifs par rapport au nombre total entré dans le modèle)
median(median$shadowMax)
[1] 2.747589
median(median$shadowMin)
[1] -2.562369
median(median$shadowMean)
[1] -0.1019566
median(median$cadmium)
[1] 6.014663
median(median$copper)
[1] 7.175817
median(median$lead)
[1] 4.469601
median(median$zinc)
[1] 5.400178
#etc...
Étape 3: Visualisation des résultats
plot(boruta.tree.2, las = 2, cex.axis = 0.7) # rouge = rejeté, bleu = ombre, vert = significatif (le plus important est dist.m, soit la distance de la meuse en mètre)
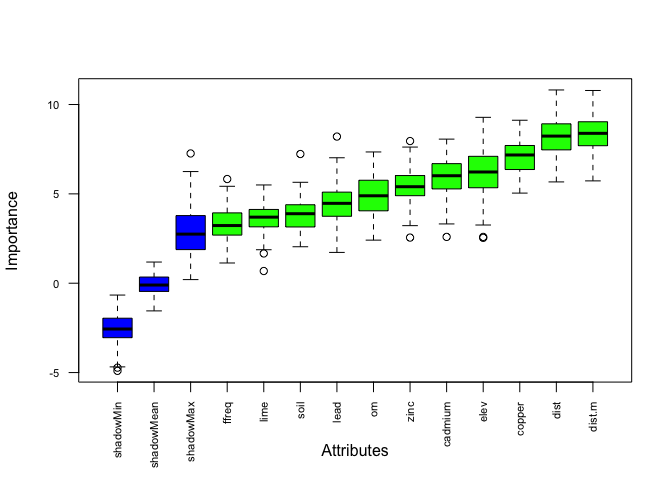
# Maintenant, quel est l'impact de la distance sur l'utilisation des terres?
#On va utiliser un graphique de dépendance partielle
landuse<- randomForest(landuse~ ., meuse, importance = T) # on ajoute les facteurs trouvés significatifs
graph.landuse<- pdp::partial(landuse,pred.var = "dist.m", which.class = "W", plot=F) #calculs du graph pour les prairies
pdp::plotPartial(graph.landuse) # le graph, yhat = probabilité de prairies, à plus de 500 m de la meuse, la probabilité d'avoir une prairie est très réduite
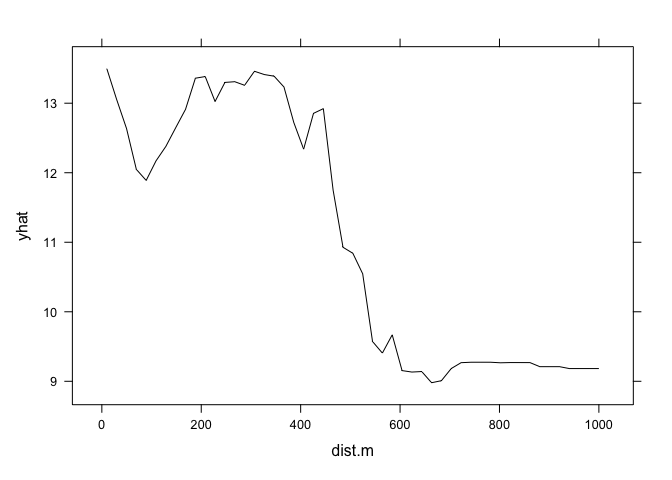
Et si nous voulions faire un graphique de dépendance partielle pour une variable explicative catégorique? Essayons-le avec le type de sol
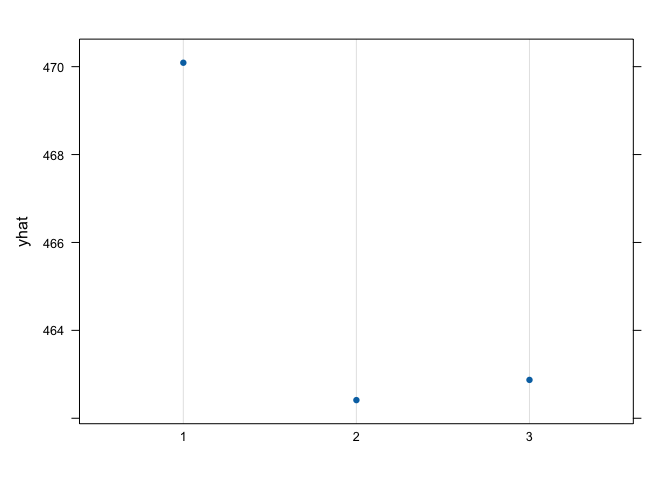
graph.landuse<- pdp::partial(landuse,pred.var = "soil", which.class = "W", plot=F) #calculer le graphique pour les prairies
pdp::plotPartial(graph.landuse) # le graphique, yhat = probabilité de prairie, La présence de sol calcaire (1) est un bon prédicteur de la présence des prairies, suivi des sol non-calcaire (2) et des sols de briques rouges (3)
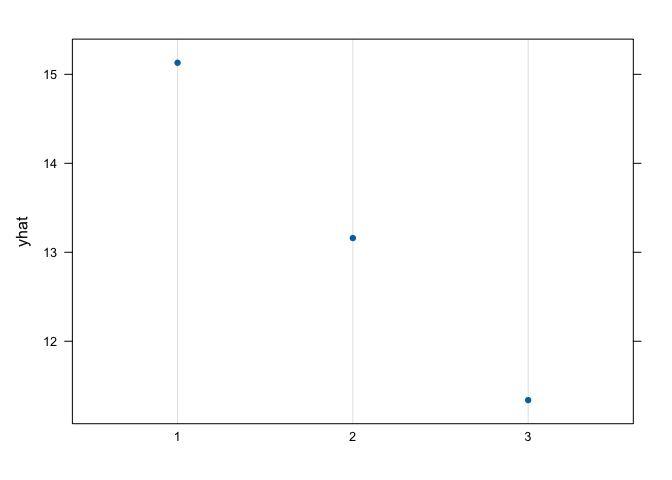
Étape 4: Le test avec valeur réponse numérique (zinc)
set.seed(666) # Ajouter de l'aléatoire et assurer la reproductibilité
boruta.tree <- Boruta(zinc~.,meuse, doTrace = 2) # le test
getSelectedAttributes(boruta.tree, withTentative = F) #le résultat
[1] "cadmium" "copper" "lead" "elev" "dist" "om" "ffreq"
[8] "soil" "lime" "dist.m"
result.boruta <- attStats(boruta.tree) # sauver les résultats dans un objet
result.boruta # Tout est confirmé sauf l'utilisation des sols
meanImp medianImp minImp maxImp normHits decision
cadmium 16.458307 16.394723 14.7122498 18.051753 1.0000000 Confirmed
copper 15.555833 15.511075 13.8689020 17.444924 1.0000000 Confirmed
lead 21.253972 21.226569 19.6326531 23.940836 1.0000000 Confirmed
elev 9.001595 9.048899 7.6848202 10.376720 1.0000000 Confirmed
dist 10.737130 10.792605 9.0666052 12.261163 1.0000000 Confirmed
om 8.033467 8.042202 6.8227216 9.728283 1.0000000 Confirmed
ffreq 5.382730 5.378091 4.1323604 6.818991 1.0000000 Confirmed
soil 5.301180 5.349173 3.9041242 6.643438 1.0000000 Confirmed
lime 6.183204 6.203087 4.7119003 7.519099 1.0000000 Confirmed
landuse 1.895212 1.883330 -0.2597717 3.966757 0.4444444 Tentative
dist.m 9.983445 9.973984 8.4906941 11.464105 1.0000000 Confirmed
boruta.tree.2 <- TentativeRoughFix(boruta.tree)
result.boruta <- attStats(boruta.tree.2) # sauver les résultats dans un objet
result.boruta # Tout est confirmé sauf l'utilisation des sols
meanImp medianImp minImp maxImp normHits decision
cadmium 16.458307 16.394723 14.7122498 18.051753 1.0000000 Confirmed
copper 15.555833 15.511075 13.8689020 17.444924 1.0000000 Confirmed
lead 21.253972 21.226569 19.6326531 23.940836 1.0000000 Confirmed
elev 9.001595 9.048899 7.6848202 10.376720 1.0000000 Confirmed
dist 10.737130 10.792605 9.0666052 12.261163 1.0000000 Confirmed
om 8.033467 8.042202 6.8227216 9.728283 1.0000000 Confirmed
ffreq 5.382730 5.378091 4.1323604 6.818991 1.0000000 Confirmed
soil 5.301180 5.349173 3.9041242 6.643438 1.0000000 Confirmed
lime 6.183204 6.203087 4.7119003 7.519099 1.0000000 Confirmed
landuse 1.895212 1.883330 -0.2597717 3.966757 0.4444444 Rejected
dist.m 9.983445 9.973984 8.4906941 11.464105 1.0000000 Confirmed
median<-data.frame(boruta.tree.2$ImpHistory)#données importantes pour rapporter les résultats, normalement, on rapporte les facteurs trouvés significatifs et le taux de réussite de l'algorithme (% de facteurs significatifs par rapport au nombre total entré dans le modèle)
median(median$shadowMax)
[1] 2.116256
median(median$shadowMin)
[1] -2.019417
median(median$shadowMean)
[1] -0.06191307
median(median$cadmium)
[1] 16.39472
median(median$copper)
[1] 15.51107
median(median$lead)
[1] 21.22657
median(median$elev)
[1] 9.048899
#etc...
Étape 5: Visualisation des résultats
plot(boruta.tree.2, las = 2, cex.axis = 0.7) # rouge = rejeté, bleu = ombre, vert = significatif (le plus important le plomb)
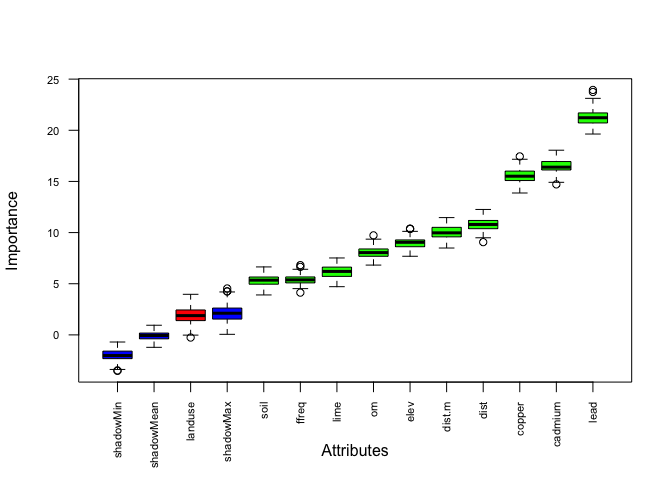
# Maintenant, quel est l'impact de la concentratration du plomb sur celle du zinc?
#On va utiliser un graphique de dépendance partielle
zinc <- randomForest(zinc ~ cadmium + copper + lead + elev +
dist + om + ffreq + soil + lime, meuse, importance = T) # on ajoute les facteurs trouvés significatifs
graph.zinc<- pdp::partial(zinc,pred.var = "lead", plot=F) #calculs du graph
pdp::plotPartial(graph.zinc) # le graph, yhat = probabilité de zinc, plus il y a de plomb et plus il y a de zinc
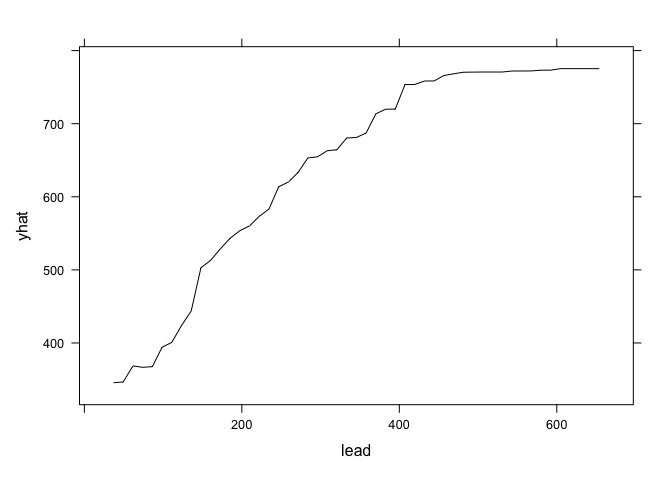
Et si nous voulions faire un graphique de dépendance partielle pour une variable explicative catégorique? Essayons-le avec le sol
graph.zinc<- pdp::partial(zinc,pred.var = "soil", plot=F) #calculer le graphique pour mai
pdp::plotPartial(graph.zinc) # le graphique, yhat = probabilité de zinc, le sol calcaire est plus contaminé en zinc que les autres