PARAFAC partie 2 : Analyse PARAFAC et validation de modèle

Jade Dormoy-Boulanger et Mathieu Michaud

Mai 2022

Une approche tridimensionnelle basée sur des matrices d’émissions et d’excitations (EEMs) peut être produite à l’aide de multiples spectres d’émission collectés successivement à longueur d’ondes d’excitation croissante. L’analyse par facteur parallèle (PARAFAC) permet ensuite de déceler les spectres d’émission et d’excitation produits par des fluorophores qui semblent se refléter dans l’ensemble des échantillons grâce aux EEMs. Les composantees de la MOD, par la présence des fluorophores, peuvent alors être identifiés et quantifiés. Une fois identifiés, les fluorophores sont associés à un processus de production, une catégorie de molécule et une provenance probable.

Il existe maintenant une base de données (Open Fluor), permettant de comparer les résultats d’analyse avec des résultats obtenus dans la littérature: https://doi:10.1039/c3ay41935e

Ce tutoriel est une adaptation du tutoriel de Matthias Pucher, qui a développé staRdom, intitulé “PARAFAC analysis of EEM data to separate DOM components in R”. Nous utiliserons les données d’exemple appelées drEEM en provenance de http://models.life.ku.dk/drEEM et converties en objet eemlist dans R, mais nous avons validé la méthode avec des données réelles également et nous sommes confiants de l’efficacité de la méthode. Vous pouvez également modifier le code pour l’importation de n’importe quel autre jeu de données EEMs à partir de MatLab.

Lien pour le tutoriel de Matthias Pucher: https://cran.r-project.org/web/packages/staRdom/vignettes/PARAFAC_analysis_of_EEM.html

La méthode dans R est équivalente à celle dans Matlab, comme le démontre cet article de Pucher et al. (2019): https://doi.org/10.3390/w11112366

Partie 2: PARAFAC

Sélectionner un modèle PARAFAC est un processus itératif qui peut demander beaucoup de temps et d’effort à votre ordinateur. Nous avons testé, à titre informatif seulement, le temps de calcul moyen pour la création du premier modèle de ce tutoriel sur plusieurs ordinateurs portables et le temps moyen jouait entre 4 min et 2 min 30. C’est d’ailleurs pour cette raison que cet atelier n’est pas en “live coding”.

Avant de commencer

La première étape est d’appeler le paquet staRdom et de vérifier le nombre de coeur de votre ordinateur. La meilleure optimisation de la vitesse des calculs est atteinte en indiquant le nombre de coeur de votre machine dans certaines fonctions plus demandantes de l’analyse. Nous utiliserons aussi les paquets dplyr, tidyr et eemR (eemR s’installe en même temps que staRdom).

#Chargement des paquets
library(staRdom)
library(dplyr)
library(tidyr)
library(eemR)
library(knitr)

#optimisation de la vitesse de calcul
cores <-detectCores(logical = FALSE) # combien de coeur sur l'ordi
cores # j'ai 6 coeurs

## [1] 4

Importation des données drEEM

#créer un nom pour des fichiers temporaires
dreem_raw <- tempfile()

# téléchargement des données drEEM à partir du répertoire de MatLab
download.file("http://models.life.ku.dk/sites/default/files/drEEM_dataset.zip",dreem_raw)

#"unzip" des données du répertoire de MatLab
dreem_data <- unz(dreem_raw, filename="Backup/PortSurveyData_corrected.mat", open = "rb") %>%
  R.matlab::readMat()

# effacer le chemin temporaire des données, car nous n'en avons plus besoin
unlink(dreem_raw)

# création d'un object eemlist
eem_list <- lapply(dreem_data$filelist.eem, function(file){
  n <- which(dreem_data$filelist.eem == file)
  file <- file %>%
    gsub("^\\s+|\\s+$", "", .) %>% # enlève les espaces dans les noms de fichier
    sub(pattern = "(.*)\\..*$", replacement = "\\1", .) # enlève les extensions des noms de fichier
  eem <- list(file = paste0("drEEM/dataset/",file),sample = file,x = dreem_data$XcRU[n,,] %>%
  as.matrix(),ex = dreem_data$Ex %>%
  as.vector(), em = dreem_data$Em.in %>%
  as.vector(), location = "drEEM/dataset/")
  class(eem) <- "eem"
  attr(eem, "is_blank_corrected") <- TRUE
  attr(eem, "is_scatter_corrected") <- FALSE
  attr(eem, "is_ife_corrected") <- TRUE
  attr(eem, "is_raman_normalized") <- TRUE
  attr(eem, "manufacturer") <- "unknown"
  eem
}) %>%
  `class<-`("eemlist")

# ajout d'un préfixe "d" au nom des fichiers, car R n'aime pas quand un nom de fichier commence par un numéro
eem_names(eem_list) <- paste0("d",eem_names(eem_list))

#Pour ce tutoriel avec drEEM, nous devons retirer les échantillons contenant "bl" et  "0A"
ol <- function(x){x==("bl") | x == "0A"}
extract <- dreem_data$sites %>% unlist() %>% ol() %>% which()
eem_list <- eem_list %>% eem_extract(extract)

## Removed sample(s): d0739sfK d0740sfK d0741sfK d0742sfK d0744sfK d1025sf
d1026sf d1027sf d1034sf d1036sf d1344sf d1345sf d1346sf d1348sf d1431sf d1433sf

Maintenant que nous avons les données, elles sont presque prêtes à être utilisées. La dernière étapes est de retirer la dispersion

eem_list <- eem_rem_scat(eem_list, remove_scatter = c(TRUE, TRUE, TRUE, TRUE), remove_scatter_width = c(15,15,18,19),
 interpolation = F, cores = cores)

Ensuite, il est toujours préférable de vérifier nos données une dernière fois avant de continuer vers le PARAFAC avec la fonction eem_checkdata() (n’est pas montré ici)

Si la fonction eem_checkdata nous indiquent qu’il y a trop de NAs, nous avons 2 choix afin d’avoir une analyse PARAFAC plus fiable: les interpoler ou utiliser un plus grand nombre d’initiation (nous verrons comment faire plus tard dans l’atelier). Dans notre cas, ils seront interpolés à la prochaine étape.

Plage de longueurs d’ondes du jeu de données

Pour des analyses PARAFAC, tout les échantillons doivent être similaires en terme de longueur d’ondes pairées. Pour palier à cette évantualité, il existe deux méthodes:

Si vous avez beaucoup de données, nous conseillons eem_red2smallest, afin d’éviter l’interpolation. Si vous avez un petit jeux de données, optez plutôt pour eem_2largest, avec interpolation.

eem_extend2largest(eem_list, interpolation = T)

#ici, comme la sortie de la fonction est imposante, elle n'est pas montrée

Trouver et retirer le bruit dans les données de EEMs

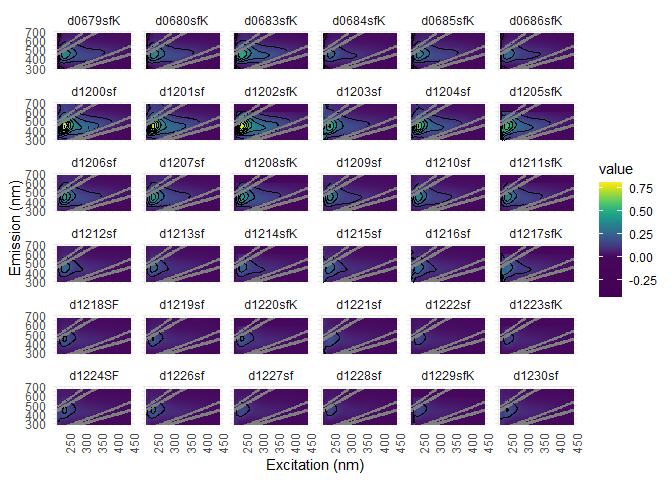
Une bonne manière de trouver bruit dans nos données de EEMs est la visualisation des échantillons. Vous pouvez utiliser la fonction eem_overview_plot() pour ce faire.

eem_overview_plot(eem_list, contour = T, spp=36)

## [[1]]


##
## [[2]]


##
## [[3]]


##
## [[4]]


##
## [[5]]


##
## [[6]]

Les fonctions suivantes, en rappel de la première partie de l’atelier PARAFAC, peuvent aider à retirer les bruits indésirables:

Pour avoir une meilleure idée de la visualisation du processus de retrait de la dispersion, nous allons faire un exemple avec l’échantillon d667sf. Afin d’extraire cet échantillon seulement, l’expression “^d667sf$” sera utilisée. ^ représente le début du string et $ la fin. Si ces caractères ne sont pas utilisés, vous risquez d’avoir tout les échantillons contenant ces caractères d’extraits.

eem_list %>%
  eem_extract(sample = "^d667sf$", keep = TRUE) %>%
  ggeem(contour = TRUE)

## Extracted sample(s): d667sf

## Warning: Removed 930 rows containing non-finite values (stat_contour).

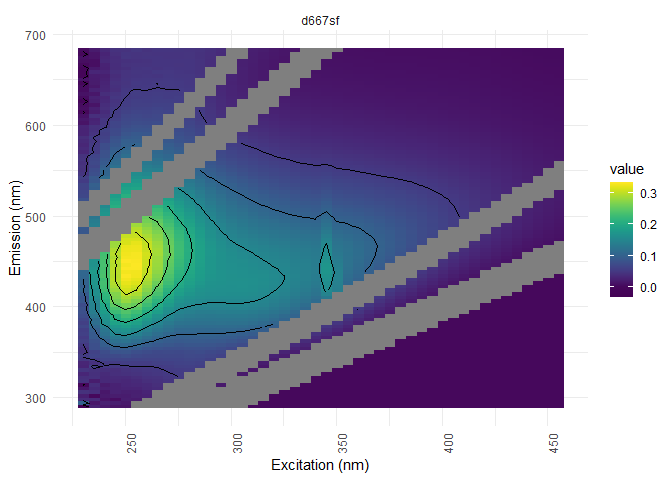
La plage du bruit visible est sous les 250 nm d’excitation et au-dessus des 580 nm d’émission (ressemble à des vagues). Ce bruit peut être retiré du jeu de données avec le code suivant:

eem_list <- eem_list %>%
  eem_setNA(sample = 176, ex = 345:350, interpolate = FALSE) %>%
  eem_setNA(em = 560:576, ex = 280:295, interpolate = FALSE)

# interpolation des NAs générés lors du retrait du bruit
eem_list <- eem_interp(eem_list, type = 1, extend = FALSE, cores = cores)

Le vrai PARAFAC commence

ATTENTION! Les résultats obtenus dans cet atelier ne sont pas optimaux. Veuillez prendre en compte la démarche et non les résultats. Ne pas se fier aux résultats!

Il est très important de trouver le bon nombre de composantes, afin d’avoir une analyse PARAFAC fiable. Si l’analyse comprend trop de composantes, alors il se peut qu’une ou plusieurs d’entre elles soient séparées en deux. Dans le cas contraire, un trop petit nombre de composantes peut mener à une perte d’information importante. Pour aider à trouver le bon nombre de composante, nous pouvons calculer et comparer une série de modèles PARAFAC. Dans l’exemple que nous vous présenterons aujourd’hui, 5 modèles ayant de 3 à 7 composantes seront calculés.

Afin d’optimiser les composantes et de réduire les erreurs résiduelles fonctionnelles, les calculs du PARAFAC utilisent un algorithme de moindre carré alternatif. Dépendamment de la valeur aléatoire de départ, différents minimums d’erreur résiduelle peuvent être trouvés. Pour avoir le minimum global, un nombre défini d’initialisation nstart est entré dans l’analyse, afin de séparer les calculs de modèles. Le modèle avec la plus petite erreur résiduelle est ensuite utilisé pour continuer les analyses PARAFAC. 25 est parfait pour l’exemple d’aujourd’hui, mais un nombre plus élevé (e.g. 50) est suggéré pour des analyses plus poussées.

Quelques unes de ces initialisations aléatoires peuvent ne pas converger. S’il y a cependant assez de modèles convergents, alors les résultats sont fiables. S’il y a moins de 50% de convergence, alors la fonction eem_parafac() émettra un avertissement. Nous vous conseillons alors d’augmenter le nombre d’initialisation aléatoire nstart.

Aussi, vous pouvez diminuer le temps de calcul dans R en spécifiant à la fonction eem_parafac le nombre de coeur de votre ordinateur via l’argument cores.

Également, un nombre maximum d’itération élevé maxit et une plus basse tolérance ctol augmentent la précision du modèle, mais augmentent également le temps de calcul. Pour le modèle final, une tolérance entre 10^-8^ et 10^-10^ est conseillée et ne devrait jamais être plus haute que 10^-6^.

Dans cet exemple, nous poserons également la contrainte d’un fluorescence non négative (nonneg). Plusieurs contraintes peuvent être imposées, via l’argument const de la fonction eem_parafac(). Les plus courantes sont:

Pour plus de contraintes, vous pouvez consulter la liste complète avec la commande CMLS::const().

Finalement, les modes de PARAFAC peuvent être mis à l’échelle, dans le but que le maximum ne dépasse pas 1. De cette manière, les effets peuvent être plus facile à voir graphiquemenet. Ceci est fait automatiquement dans le mode A (les échantillons). Dans le cas de hauteurs de pics de fluorescence inégales, la fonction eempf_rescaleBC() peut également ajuster les modes B (longueurs d’onde d’émissions) et C (longueur d’onde d’excitation), afin d’améliorer la visualisation des graphiques. D’autres fonctions sont également disponibles et décrite dans le tutoriel de Matthias Pucher: https://cran.r-project.org/web/packages/staRdom/vignettes/PARAFAC_analysis_of_EEM.html

# minimum de composantes
dim_min <- 3

# maximum de composantes
dim_max <- 7

#nombre de modèles similaires desquels le meilleur est sélectionné
nstart <- 25

#nombre maximum d'itération dans l'analyse PARAFAC
maxit = 5000

#tolérance de l'analyse PARAFAC
ctol <- 10^-6

#calcul des modèles, un pour chaque nombre de composante.
#Plusieurs avertissements apparaîtront, demandant à augmenter nstart....
#ce qui sera fait à la dernière étape
pf1n <- eem_parafac(eem_list, comps = seq(dim_min,dim_max), normalise = FALSE,
const = c("nonneg", "nonneg", "nonneg"), maxit = maxit, nstart = nstart, ctol = ctol, cores = cores)

#remise à l'échelle des modes B et C à un maximum de fluorescence de 1 pour chaque composante
pf1n <- lapply(pf1n, eempf_rescaleBC, newscale = "Fmax")

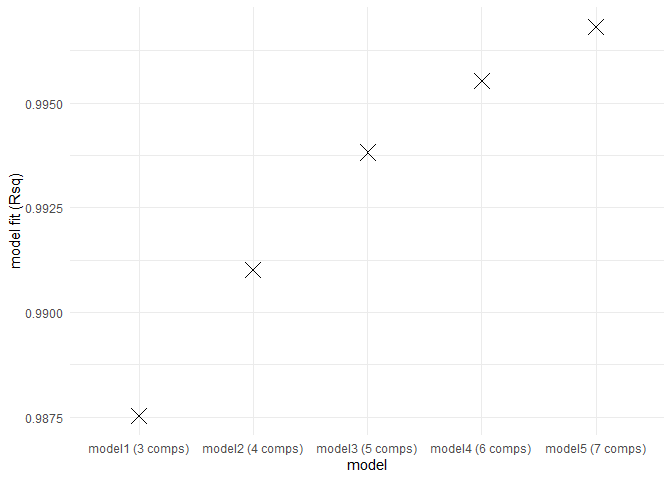
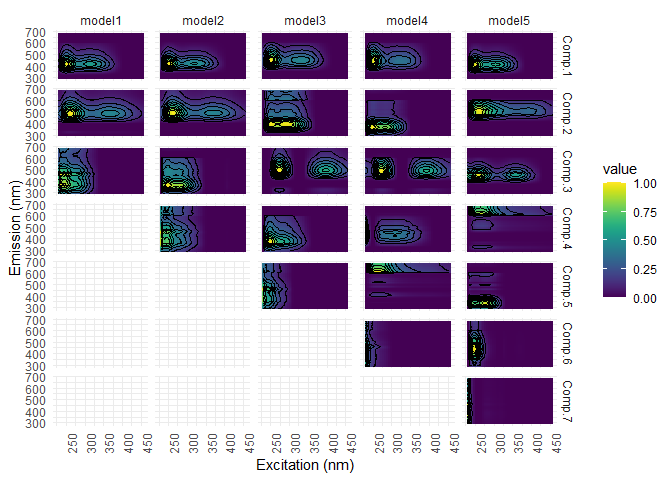
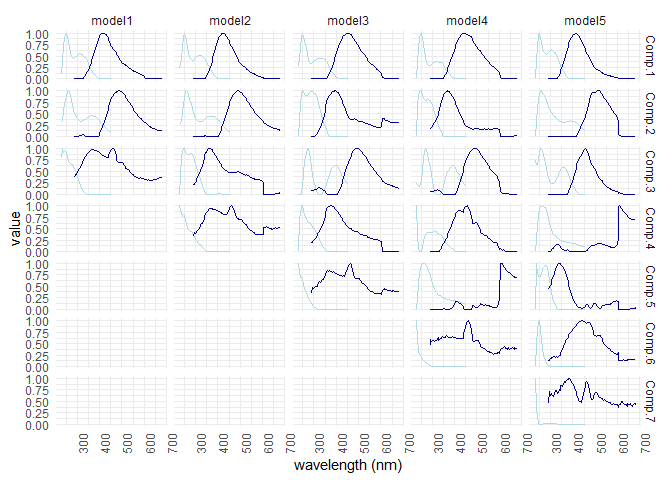
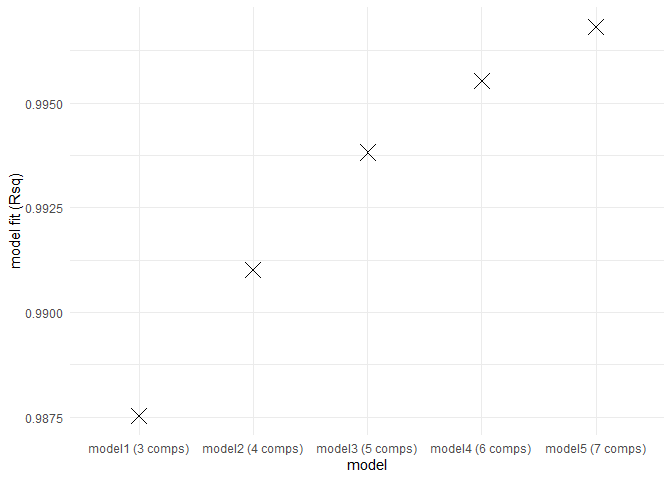
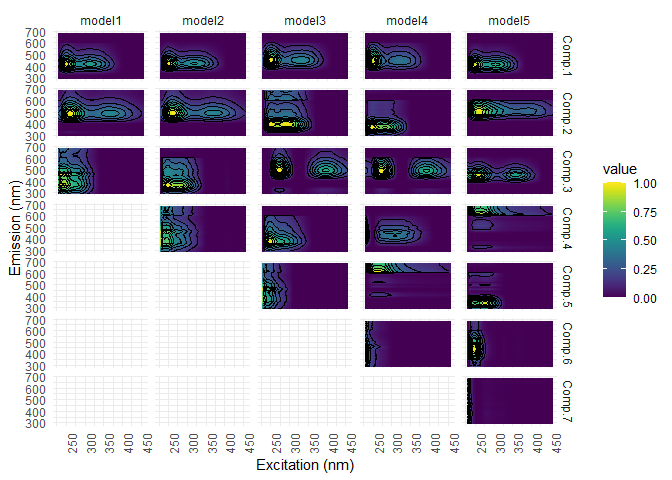
eempf_compare() permet de mettre en graphique chaque modèle précédement créés. Le premier graphique montre les R^2^, le deuxième et le troisième montrent les modèles sous deux angles différents. Dans le troisième, les lignes pâles sont les longueurs d’onde d’excitation et les foncées sont celles d’émissions. Gardez en tête que l’on veut un modèle bien ajusté ( haut R^2^), mais pas sur-ajusté (R^2^ de plus de 1). Le modèle 4 (6 comoposantes) est le meilleur modèle dans ce cas-ci.

eempf_compare(pf1n, contour = TRUE)


## [[1]]


##
## [[2]]


##
## [[3]]


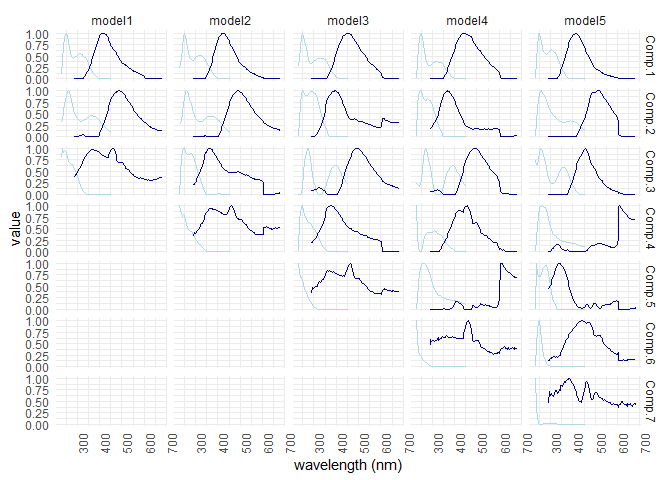
# à noter ici que la fonction sortira 6 graphique, soit deux fois les mêmes, nous ne savons pas pourquoi

Vérification de la corrélation entre les différents composantes

L’agorithme du PARAFAC assume, par défaut, qu’il n’y a pas de corrélation entre les différents composantes. Si les concentrations en carbone organique dissous ont de grandes différences entre les échantillons, alors une corrélation entre les composantes est plus probable. Pour éviter tout problème, les échantillons peuvent être normalisés. Rappelez-vous que nous avons sélectionné le modèle 4.

# vérification de la corrélation entre les composantes en table
eempf_cortable(pf1n[[4]], normalisation = FALSE)

##           Comp.1    Comp.2     Comp.3    Comp.4      Comp.5     Comp.6
## Comp.1 1.0000000 0.9644792 0.80409005 0.7432977  0.44823885  0.2997809
## Comp.2 0.9644792 1.0000000 0.70289853 0.6805600  0.51421121  0.1917911
## Comp.3 0.8040901 0.7028985 1.00000000 0.3307425  0.04936569  0.2788050
## Comp.4 0.7432977 0.6805600 0.33074247 1.0000000  0.58136937  0.3778630
## Comp.5 0.4482389 0.5142112 0.04936569 0.5813694  1.00000000 -0.2952439
## Comp.6 0.2997809 0.1917911 0.27880502 0.3778630 -0.29524388  1.0000000

#vérification de la corrélation entre les composantes en graphique
eempf_corplot(pf1n[[4]], progress = FALSE, normalisation = FALSE)

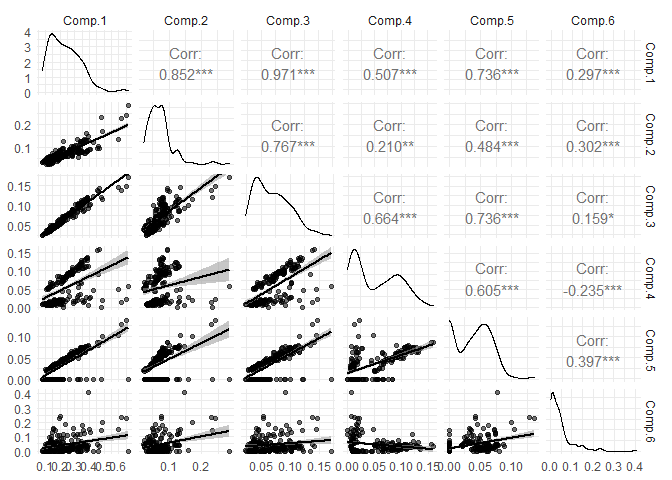
Comme certaines des composantes sont très corrélées, nous allons recalculer le modèle, mais avec une normalisation des données. Plus loin dans l’analyse, la normalisation sera enlevée automatiquement en multipliant les modes A avec les facteurs de normalisation pour les exportations et les graphiques.

#nouveaux modèles PARAFAC avec normalisation des données.
#Plusieurs avertissements apparaîtront, demandant à augmenter nstart....
#ce qui sera fait à la dernière étape
pf2 <- eem_parafac(eem_list, comps = seq(dim_min,dim_max), normalise = TRUE,
const = c("nonneg", "nonneg", "nonneg"), maxit = maxit, nstart = nstart, ctol = ctol, cores = cores)

#remise à l'échelle des modes B et C à un maximum de fluorescence de 1 pour chaque composante
pf2 <- lapply(pf2, eempf_rescaleBC, newscale = "Fmax")

# les nouveaux modèles normalisés
eempf_plot_comps(pf2, contour = TRUE, type = 1)

Trouver et exclure les valeurs aberrantes

L’effet de levier causé par des valeurs aberrantes peuvent diminuer la fiabilité d’un modèle PARAFAC en “tirant” les analyses vers cette valeur. Cet effet de levier peut être corrigé en retirant les données aberrantes de nos échantillons. Pour ce faire, deux méthodes peuvent être employées:

  1. eempf_leverage(), permet de calculer l’effet de levier et eempf_leverage_plot(), de créer un graphhique pour la sélection des valeurs aberrantes. Les valeurs aberrantes seront au-dessus des autres dans les graphiques. Ensuite, on peut simplement créer une liste avec les valeurs aberrantes trouvées, et les exclure des échantillons. Cette manière sera montrée en exemple.

  2. eempf_leverage_ident() crée trois graphiques interactifs où il est possible, suite au calcul de l’effet de levier avec eempf_leverage(), d’exclure manuellement les données aberrantes en cliquant dessus. Pour changer de graphique et pour terminer, utilisez la touche esc de votre clavier. Si vous utilisez la commande suivante pour créer vos graphique interactifs, alors les valeurs sur lesquelles vous aurez appuyé seront sauvées dans un objet appellé “exclude”: exclude <- eempf_leverage_ident(cpl,qlabel=0.1)

#calcul de l'effet de levier
cpl <- eempf_leverage(pf2[[4]])

#graphique des valeurs aberrantes
eempf_leverage_plot(cpl,qlabel=0.1)


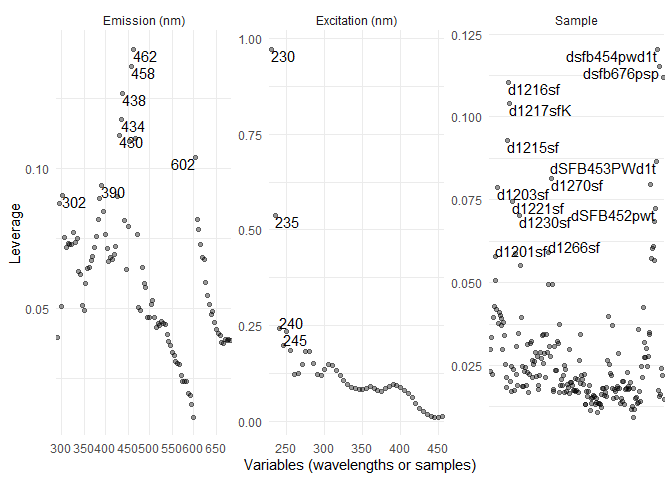
#création de liste d'exclusion des valeurs aberrantes

exclude <- list("ex" = c(),
                "em" = c(),
                "sample" = c("dsfb676psp","dsgb447wt")
)

#exclusion du jeu de données
eem_list_ex <- eem_exclude(eem_list, exclude)

Suite à l’exclusion des données aberrantes, il faut générer à nouveau un modèle PARAFAC et revérifier les valeurs aberrantes.

#création d'un nouveau PARAFAC. Plusieurs avertissements apparaîtront, demandant à augmenter nstart....
# ce qui sera fait à la dernière étape
pf3 <- eem_parafac(eem_list_ex, comps = seq(dim_min,dim_max), normalise = TRUE,
maxit = maxit, nstart = nstart, ctol = ctol, cores = cores)
pf3 <- lapply(pf3, eempf_rescaleBC, newscale = "Fmax")

#visualisation
eempf_plot_comps(pf3, contour = TRUE, type = 1)


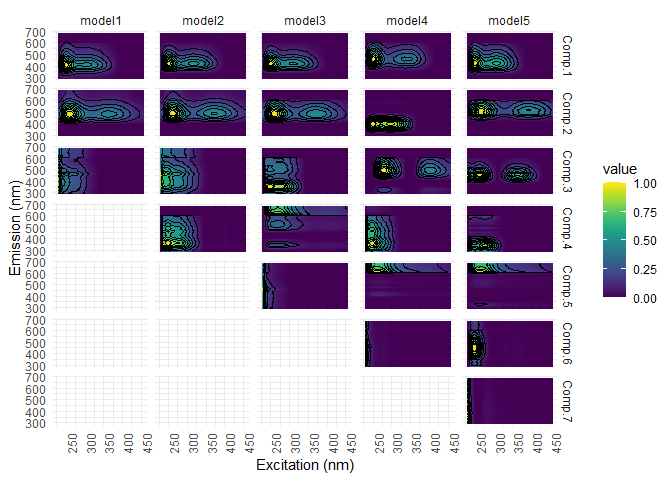
#revérification des données aberrantes
eempf_leverage_plot(eempf_leverage(pf3[[4]]),qlabel=0.1)

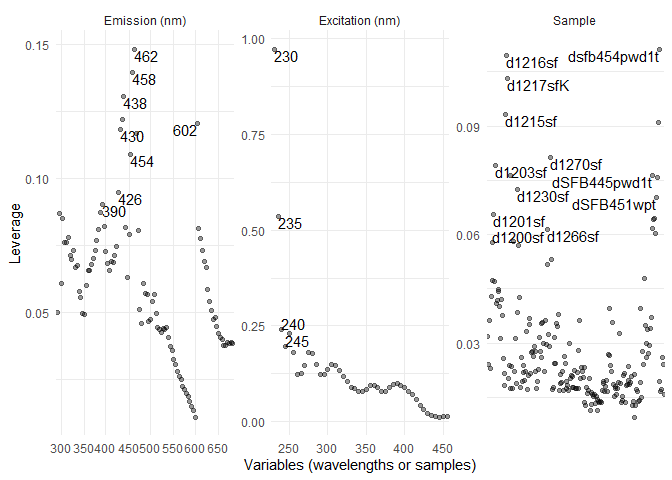
Recalculer le modèle avec plus de précision

Comme déjà mentionné, une plus grande précision du modèle demande un plus grand temps de calcul. Pour cette raison, la tolérance est baissée dans les dernières étapes seulement. Nous recalculerons seulement le modèle 4 (6 composantes). De plus, nous utiliserons l’argument strictly_converging = TRUE, afin de déduire un nombre significatif de modèles convergent. Si vous mettez FALSE, veuillez vérifiez le ratio des modèles convergents et vous assurez que le meilleur est choisi (nous ne recommandons pas cette otpion!)

#abaissement de la tolérance
ctol <- 10^-8

#nombre de modèles similaires desquels le meilleur est sélectionné
nstart <- 25

#nombre maximum d'itération dans l'analyse PARAFAC
maxit = 10000

#création du nouveau modèle
pf4 <- eem_parafac(eem_list_ex, comps = 6, normalise = TRUE, const = c("nonneg", "nonneg", "nonneg"), maxit = maxit,
 nstart = nstart, ctol = ctol, output = "all", cores = cores, strictly_converging = TRUE)

pf4 <- lapply(pf4, eempf_rescaleBC, newscale = "Fmax")

#vérification de la convergence
eempf_convergence(pf4[[1]])

## Calculated models:  25
## Converging models:  25
## Not converging Models, iteration limit reached:  0
## Not converging models, other reasons:  0
## Best SSE:  8241.902
## Summary of SSEs of converging models:
##    Min. 1st Qu.  Median    Mean 3rd Qu.    Max.
##    8242    8242    8242    8343    8339    9893

#vérification des valeurs aberrantes
eempf_leverage_plot(eempf_leverage(pf4[[1]]))


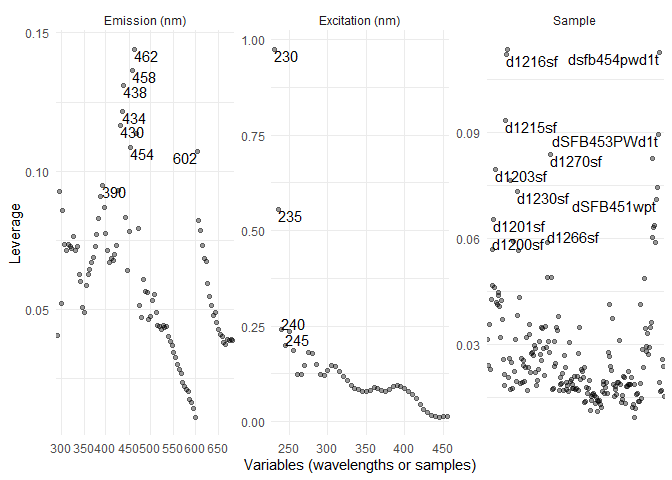
#vérification de la corrélation
eempf_corplot(pf4[[1]], progress = FALSE)

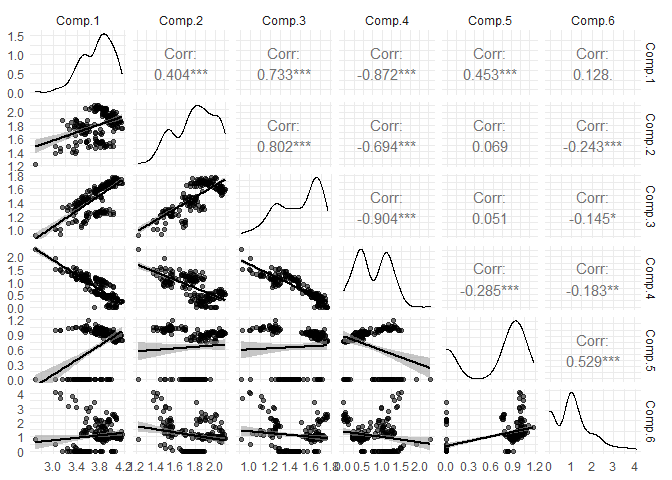
Répétez les étapes de création jusqu’à entière satisfaction des résultats

Graphiques des résultats

Les graphiques suivants présentent deux informations cruciales: le premier graphique indique la forme des composantes et donne des indications sur leur composition et le deuxième donne des informations sur leur quantité dans les différents échantillons.

eempf_comp_load_plot(pf4[[1]], contour = TRUE)

## [[1]]


##
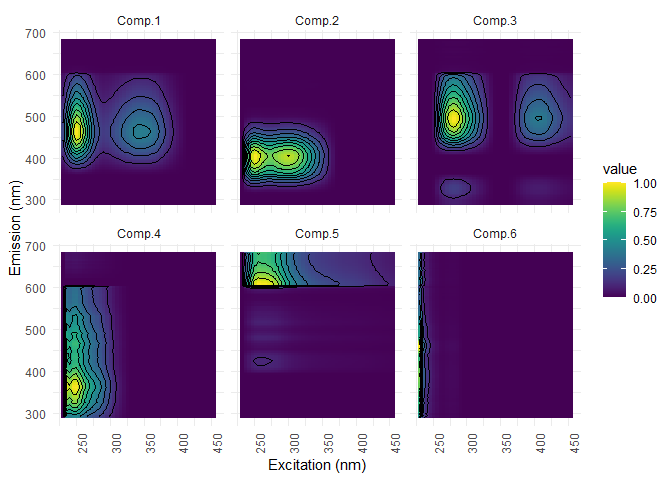
## [[2]]

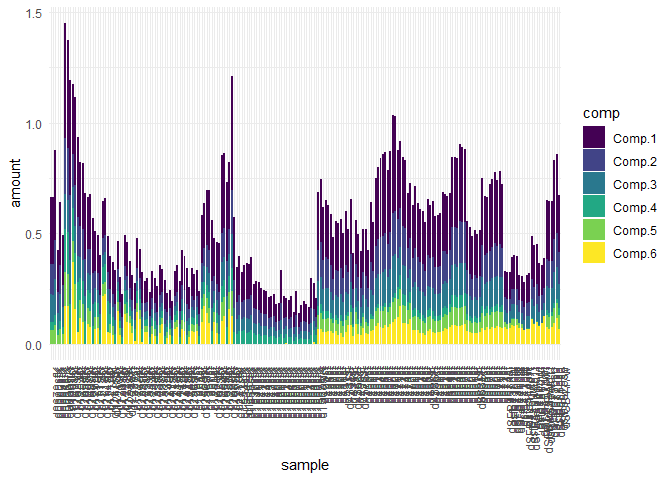
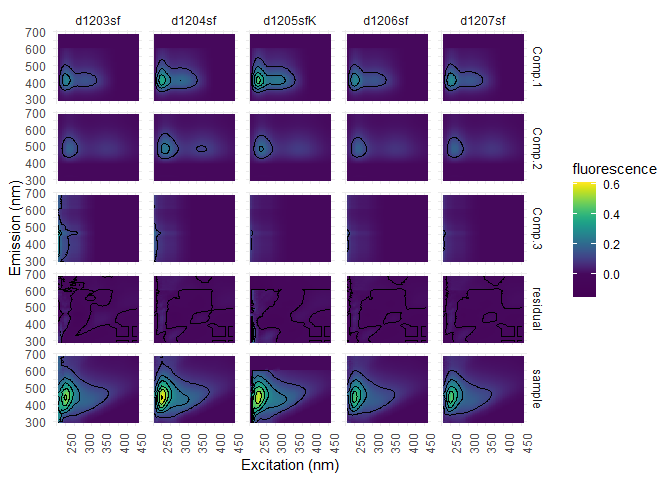
Représentation graphique des échantillons et leur résidus

Les colonnes représentes les échantillons et les lignes les composantes (3), les résidus et les échantillons. Nous avons utilisé pf3, car ce modèle contient encore les valeurs aberrantes, qui peuvent être interessantes à évaluer.

eempf_residuals_plot(pf3[[1]], eem_list, select = eem_names(eem_list)[10:14], cores = cores, contour = TRUE)

## [[1]]

Analyse de stabilité

L’analyse de stabilité permet de vérifier la stabilité du modèle. Les données sont recombinées de 6 différentes manières et les résultats des 6 recombinaisons devraient êtres similaires. L’analyse est très longue!

#l'analyse de stabilité
sh <- splithalf(eem_list_ex, 6, normalise = TRUE, rand = FALSE, cores = cores,
  nstart = nstart, strictly_converging = TRUE, maxit = maxit, ctol = ctol)

#le graphique
splithalf_plot(sh)

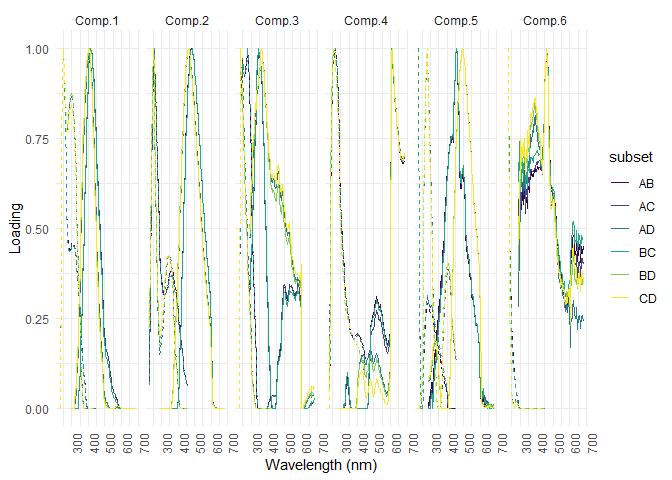
Le facteur de congruence de Tucker est aussi un outil pour tester la similarité. Un facteur de 1 représente une similarité parfaite.

#création de la table
tcc_sh_table <- splithalf_tcc(sh)

#la table
tcc_sh_table

##    component   comb    tcc_em    tcc_ex
## 1     Comp.1 ABvsCD 0.9636640 0.9106166
## 2     Comp.1 ACvsBD 0.9572791 0.9578393
## 3     Comp.1 ADvsBC 0.9357480 0.9499169
## 4     Comp.2 ABvsCD 0.9459329 0.9804946
## 5     Comp.2 ACvsBD 0.8095131 0.9910280
## 6     Comp.2 ADvsBC 0.9601128 0.9378207
## 7     Comp.3 ABvsCD 0.8964998 0.8776356
## 8     Comp.3 ACvsBD 0.9004275 0.8864507
## 9     Comp.3 ADvsBC 0.5896461 0.9826212
## 10    Comp.4 ABvsCD 0.9955484 0.9428685
## 11    Comp.4 ACvsBD 0.6931107 0.7651759
## 12    Comp.4 ADvsBC 0.9152928 0.8807036
## 13    Comp.5 ABvsCD 0.5522928 0.9458636
## 14    Comp.5 ACvsBD 0.9978789 0.9919176
## 15    Comp.5 ADvsBC 0.9949597 0.9688262
## 16    Comp.6 ABvsCD 0.9285425 0.9897605
## 17    Comp.6 ACvsBD 0.9597023 0.9946536
## 18    Comp.6 ADvsBC 0.9510946 0.9814227

Plusieurs autres formes de validation de modèles sont décrites dans le tutoriel de Matthias Pucher au point 8.13: https://cran.r-project.org/web/packages/staRdom/vignettes/PARAFAC_analysis_of_EEM.html

Format du modèle

Nommer le modèle et les composantes

Personnaliser le graphique est important pour la compréhension et la visualisation du modèle.

# obtenir les noms des modèles présentement (il n'y en a pas!!)
names(pf3)

## NULL

#nommer les différentes modèles (attention, le nombre de modèles doit être égale au nombre de noms)

names(pf3) <- c("3 components", "4 components xy","5 components no outliers","6 components","7 components")

names(pf3)

## [1] "3 components"             "4 components xy"         
## [3] "5 components no outliers" "6 components"            
## [5] "7 components"

# obtenir les noms des composantes de notre modèle final
eempf_comp_names(pf4)

## [[1]]
## [1] "Comp.1" "Comp.2" "Comp.3" "Comp.4" "Comp.5" "Comp.6"

#remplacer les noms de notre modèle final
eempf_comp_names(pf4) <- c("A4","B4","C4","D4","E4","F4")

#remplacer les noms des composantes dans le cas de plusieurs modèles (ex: pf3)
eempf_comp_names(pf3) <- list(c("A1","B1","C1"),
                                       c("humic","T2","whatever","peak"),
                                       c("rose","peter","frank","dwight","susan"),
                                       c("A4","B4","C4","D4","E4","F4"),
                                       c("A5","B5","C5","D5","E5","F5","G5"))

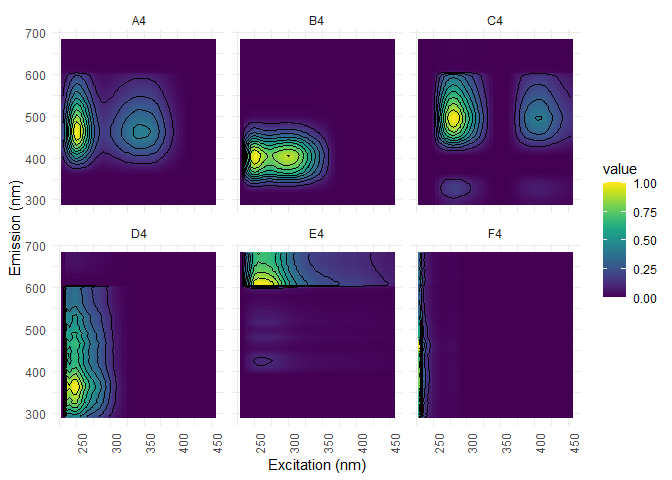
#le graphique de notre modèle final avec les nouveaux noms
pf4[[1]] %>%
  ggeem(contour = TRUE)

Exportation et interprétation du modèle

Noter que le tutoriel de Matthias Pucher offre d’autre possibilités que celle présentée dans cet atelier: https://cran.r-project.org/web/packages/staRdom/vignettes/PARAFAC_analysis_of_EEM.html

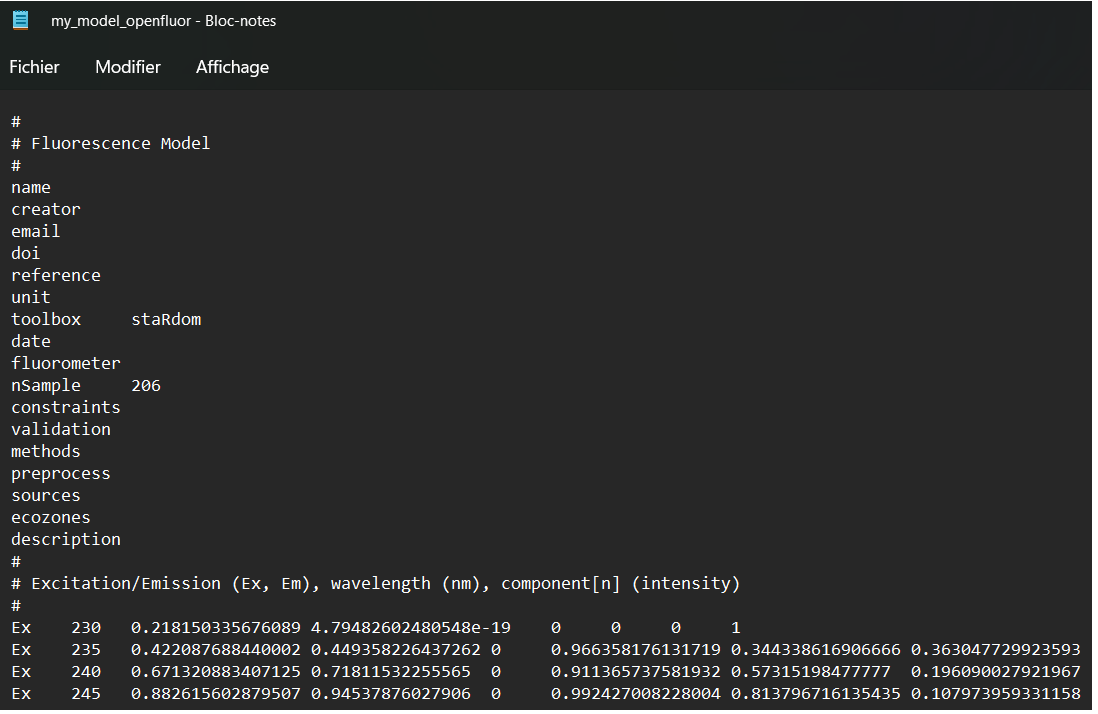
Comparaison avec la base de données openfluor.org

eempf_openfluor() peut exporter sous forme txt notre modèle PARAFAC. Ensuite ce fichier peut être téléversé sur openfluor.org et comparé aux autres données de la base. Attention de bien vérifier les en-tête du fichier exporté, car certaines valeurs ne sont pas réglées automatiquement.

eempf_openfluor(pf4[[1]], file = "my_model_openfluor.txt")

## An openfluor file has been successfully written. Please fill in missing header fields manually!

Créer le rapport du PARAFAC

Le rapport créé par eempf_report() contient les informations importantes du modèle, ainsi que les résultats. Il est exporté en html. Vous pouvez aussi spécifier les informations qu’il contiendra.

eempf_report(pf4[[1]], export = "parafac_report.html", eem_list = eem_list_ex, shmodel = sh, performance = TRUE)

##
##
## processing file: PARAFAC_report.Rmd

## output file: PARAFAC_report.knit.md

##
## Output created: parafac_report.html

Exportation du modèle

eempf_export() permet d’exporter un fichier csv avec les matrices du modèle.

eempf_export(pf4[[1]], export = "parafac_report.csv")

Fin