Resource selection function
Riwan Leroux
Avril 2022
- Introduction
- Préparation de la base de données pour construire les RSF
- Modèle RSF
- Post-analyses et interprétations rapides
- Bibliographie
Introduction
Le cadre des analyses de sélection est adapté pour traiter l’énorme quantité de données à haute fréquence générées par de telles avancées technologiques (par exemple, la fonction de sélection des ressources - RSF, la fonction de sélection des pas - SSF - Thurfjell et al. 2014, Fieberg et al. 2021, Munden et al. 2021). Ce cadre d’analyse repose sur la comparaison entre l’utilisation réelle de l’habitat ou les déplacements réels de l’animal et l’utilisation ou les déplacements d’un animal virtuel qui se déplacerait de manière aléatoire dans un environnement (Fieberg et al. 2021). Ce faisant, l’animal virtuel rencontrera des caractéristiques écologiques qui pourraient être similaires ou différentes de ce qu’un animal réel a rencontré (par exemple, la température, le biotope, la densité des ressources, etc.). Il est alors possible de déterminer s’il y a ou non sélection de caractéristiques particulières par l’animal suivi.
Etude de cas
Dans cette étude, nous nous sommes concentrés sur le lac Ledoux, un petit lac boréal où la seule espèce de poisson est l’omble de fontaine (Salvelinus fontinalis), un poisson sténotherme froid. Ses principales proies sont le zooplancton dans les zones pélagiques et le zoobenthos dans les zones littorales (Magnan 1988, Bourke et al. 1999). Des études antérieures suggèrent que l’omble de fontaine ne peut pas accéder à l’épilimnion donc au grand bassin peu profond du lac Ledoux durant l’été à cause de la température au-dessus de son seuil létal de 22°C (Bourke et al. 1996; Bertolo et al. 2011; Goyer et al. 2014) . Pour faire face au stress thermique, les poissons présentent une thermorégulation comportementale variable selon les individus (Goyer et al. 2014). Ces variations individuelles pourraient donc impliquer des différences individuelles dans la stratégie d’alimentation. Pour comprendre comment les poissons combinent leurs impératifs de thermorégulation avec la recherche de ressources, nous avons utilisé l’analyse de sélection des ressources (RSF ; Boyce & Macdonald 1999 ; Fieberg et al 2021).
Pour retrouver les bases de donnéees nécessaires à l’exécution de cet atelier allez voir à :
https://github.com/RiwanLeroux/Numerilab.git
Tout d’abord, visualisons comment, dans notre cas d’étude, un poisson s’est déplacé pendant 4h à l’été 2018 dans le lac Ledoux. Le but ultime de ce type d’analyse est de comprendre si oui ou non un animal sélectionne certaines variables environnementales (e.g. zooplancton, distance aux zones littorales, …).
#Importer base de données poisson
load("Fish72.Rdata")
fish<-Fish72; rm(Fish72)
#Importer le raster du lac pour représenter graphiquement les localisations du poisson sur a carte
load("Bathymetry_Ledoux.Rdata")
#Regarder la structure du tableau de données poisson
head(fish)
## posix_est X Y Depth Name burst
## 27993 2018-08-06 12:00:10 1173.186 884.1521 4.662200 Fish72 1
## 27994 2018-08-06 12:00:23 1169.096 883.1159 4.662200 Fish72 1
## 27995 2018-08-06 12:00:36 1165.661 882.2736 4.662200 Fish72 1
## 27996 2018-08-06 12:00:49 1163.142 881.3348 4.740966 Fish72 1
## 27997 2018-08-06 12:01:14 1158.561 879.4407 4.889798 Fish72 1
## 27998 2018-08-06 12:01:36 1155.120 878.0975 5.036059 Fish72 1
#Représenter le raster
image(ledoux_depth,col=palette,ylim=c(780,1150),main="The 596 locations of the Fish recorded in 4h")
#Ajouter les localisations de poisson sur la carte
points(fish$X,fish$Y,pch=16,cex=0.7)
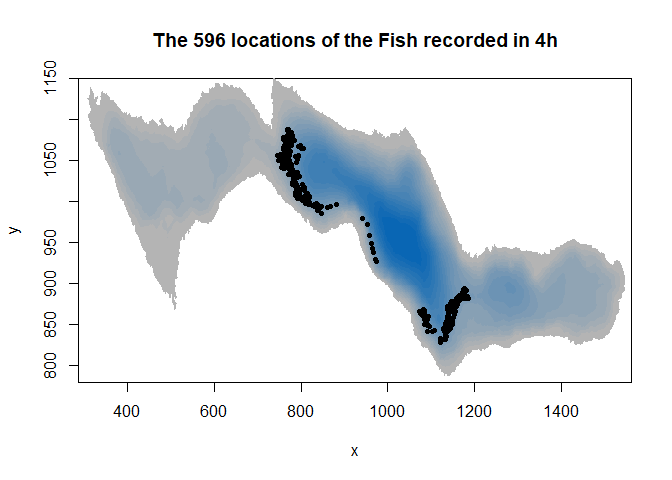
A noter que notre poisson est représenté en 2D mais se déplace en 3D. La troisième dimension n’est pas encore implémentée dans les packages traitant de la fonction de sélection des ressources, mais voyons ce qui pourra être fait plus tard.
Fondamentalement, il existe deux approches : l’analyse de la sélection des ressources ou de pas. La première utilise un polygone convexe minimale pour échantillonner des points afin d’imiter des emplacements aléatoires et la seconde construit des pas aléatoires pour chaque pas de l’animal.
La fonction de sélection de pas intégrant des paramètres de mouvement tels que la longueur de pas et les angles de virage compare chaque pas observé à partir d’une trajectoire avec les pas simulés associés. Ainsi, les mesures des caractéristiques de l’habitat doivent avoir une résolution plus fine que la longueur de pas moyenne pour rendre la SSF pertinente.
#Représenter le raster
image(ledoux_depth,col=palette,ylim=c(780,1150),main="Step comparison")
#Ajouter les pas observés sur la carte (longueur plus angle)
lines(fish$X[c(1:300,400,500,590)],fish$Y[c(1:300,400,500,590)],lty=4)
lines(fish$X[c(300,400)],fish$Y[c(300,400)],lwd=2)
lines(fish$X[c(400,500)],fish$Y[c(400,500)],lwd=2)
#Ajouter les pas simulés sur la carte
lines(c(fish$X[300],800),c(fish$Y[300],1050),col="red",lwd=1.5)
lines(c(fish$X[300],840),c(fish$Y[300],970),col="red",lwd=1.5)
lines(c(fish$X[300],950),c(fish$Y[300],1025),col="red",lwd=1.5)
lines(c(fish$X[400],750),c(fish$Y[400],1050),col="forestgreen",lwd=1.5)
lines(c(fish$X[400],700),c(fish$Y[400],1070),col="forestgreen",lwd=1.5)
lines(c(fish$X[400],790),c(fish$Y[400],1055),col="forestgreen",lwd=1.5)
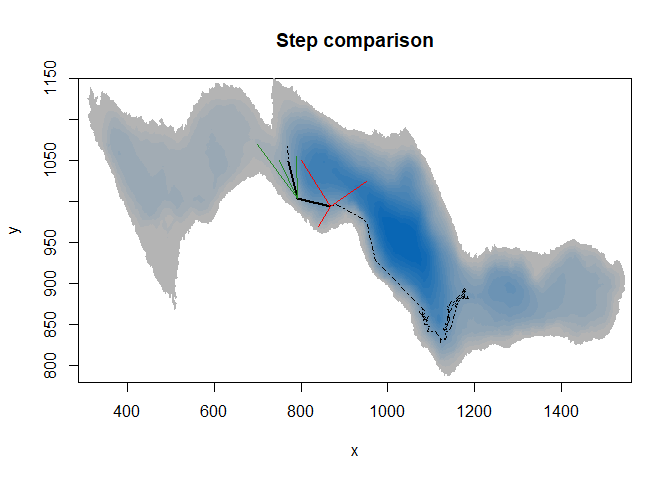
Ici, une SSF comparerait chaque pas noir observé avec les pas simulés correspondants. Si nous considérions un pas d’une minute, les pas simulés et observés se termineraient très proches les uns des autres, avec de trop petites différences dans les valeurs des variables d’environnement.
Une RSF a été privilégié par rapport à une SSF en raison de l’acquisition à haute fréquence des positions des poissons. Nous ne voulons pas réduire beaucoup notre résolution temporelle ce qui serait requis pour une SSF en raison de notre résolution d’échantillonnage des ressources.
Ici, nous faisons un mélange en construisant des trajectoires simulées au lieu de pas Cela permet de mieux prendre en compte le comportement du poisson qui peut aller à n’importe quel endroit convenable dans le lac mais en maximisant la réponse probable puisque notre résolution reste fine. Pour construire des trajectoires simulées, il faut en avoir une observée et la randomiser.
Temps de calcul demandant
Faire toutes ces validations, pour chaque animal que vous suivez, demande une énorme quantité de données donc un temps énorme. Dans mon étude, nous avons 194 trajectoires observées à tester. Le temps de calcul étant trop lourd pour être géré par un ordinateur personnel (plusieurs mois), toutes les premières étapes ont été réalisées avec des opérations parallèles (boucles foreach ; packages foreach et doParallel ; voir précédent Numerilab) sur un ordinateur multicœur (Titan S599 à 20 cœurs (+40 Threads) et 96 Go de RAM - Titan Computers). Au total, il a fallu trois semaines pour réaliser l’ensemble des 970 000 trajectoires simulées par cette approche.
Préparation de la base de données pour construire les RSF
La Trajectoire observée
Pour transformer nos localisations en trajectoire, nous utiliserons le package adehabitatLT écrit par Clément Calange (2020).
Nous avons une distribution de localisation idéale, sans localisation aberrante mais attention ! Si certains emplacements se trouvaient en dehors du lac par exemple, ils doivent être supprimés de la base de données.
# La fonction as.ltraj permet de transformer une matrice avec le temps et les lieux en une succession de pas, avec la longueur du pas, l'angle entre un pas et le précédent, la durée du pas etc.
#NB : lorsque l'on a plusieurs poissons ou périodes échantillonnés, cette fonction permet de le traiter en précisant le nom de chaque individu et le burst (c'est à dire une succession de relocalisation pour un animal précis à une date précise). Il en résultera une liste contenant toutes les trajectoires calculées.
track_fish=as.ltraj(fish[,c("X","Y")],fish$posix_est,id=fish$Name,
burst=fish$burst,slsp="missing",proj4string = crs("+proj=aeqd +lat_0=46.802927 +lon_0=-73.277817 +x_0=1000 +y_0=1000 +datum=WGS84 +units=m +no_defs"))
# Voyons ce que nous avons. Ici, on a un poisson suivi pendant quatre heures, on a juste un burst donc un élément dans la liste.
head(track_fish[[1]])
## x y date dx dy dist dt
## 27993 1173.186 884.1521 2018-08-06 12:00:10 -4.090113 -1.0361572 4.219319 13
## 27994 1169.096 883.1159 2018-08-06 12:00:23 -3.434362 -0.8422838 3.536140 13
## 27995 1165.661 882.2736 2018-08-06 12:00:36 -2.519391 -0.9387708 2.688609 13
## 27996 1163.142 881.3348 2018-08-06 12:00:49 -4.581407 -1.8941690 4.957536 25
## 27997 1158.561 879.4407 2018-08-06 12:01:14 -3.440211 -1.3431737 3.693124 22
## 27998 1155.120 878.0975 2018-08-06 12:01:36 -2.465305 -0.3790476 2.494274 11
## R2n abs.angle rel.angle
## 27993 0.00000 -2.893480 NA
## 27994 17.80265 -2.901088 -0.00760747
## 27995 60.14627 -2.784912 0.11617599
## 27996 108.81593 -2.749548 0.03536373
## 27997 236.09573 -2.769360 -0.01981231
## 27998 363.01937 -2.989034 -0.21967413
Pour éviter les biais et puisque nous ne voulons pas faire d’analyse intégrée de sélection de pas (iSSA), nous devons homogénéiser le pas de temps. Nous fixons le pas de temps à une minute et interpolons l’emplacement des poissons pour avoir l’emplacement des poissons à chaque minute. Cela a également l’avantage de réduire la base de données et de rendre l’analyse plus rapide en gardant une résolution temporelle relativement élevée.
#La fonction redisltraj nous permet d'homogénéiser chaque pas à des pas d'une minute en spécifiant la durée du pas en secondes. Il recalculera simplement les emplacements de chaque pas par interpolation.
fixed_track <- redisltraj(track_fish, 60, type="time")
head(fixed_track[[1]])
## x y date dx dy dist dt
## 1 1173.186 884.1521 2018-08-06 12:00:10 -13.892248 -4.408314 14.574903 60
## 2 1159.294 879.7437 2018-08-06 12:01:10 -10.792783 -2.036087 10.983161 60
## 3 1148.501 877.7077 2018-08-06 12:02:10 -7.391698 -4.630913 8.722532 60
## 4 1141.109 873.0767 2018-08-06 12:03:10 -3.540374 -4.736066 5.913084 60
## 5 1137.569 868.3407 2018-08-06 12:04:10 2.804164 -10.162361 10.542149 60
## 6 1140.373 858.1783 2018-08-06 12:05:10 -3.327717 -8.881346 9.484303 60
## R2n abs.angle rel.angle
## 1 0.0000 -2.834321 NA
## 2 212.4278 -2.955131 -0.1208105
## 3 650.8811 -2.581914 0.3732175
## 4 1151.5791 -2.212718 0.3691962
## 5 1518.5778 -1.301560 0.9111579
## 6 1751.3242 -1.929292 -0.6277319
Regardons ce que ça donne !
#Représenter la carte bathymétrique en fond, avec un grossissement sur la zone utilisée
image(ledoux_depth,col=palette,ylim=c(800,1100),xlim=c(700,1200),main="Raw location vs. Fixed track")
#Ajouter les localisations du poisson
points(fish$X,fish$Y,pch=16,cex=0.7)
#Ajouter la trajectoire calculée du poisson suivi
lines(fixed_track[[1]]$x,fixed_track[[1]]$y,col="salmon",lwd=1.5)
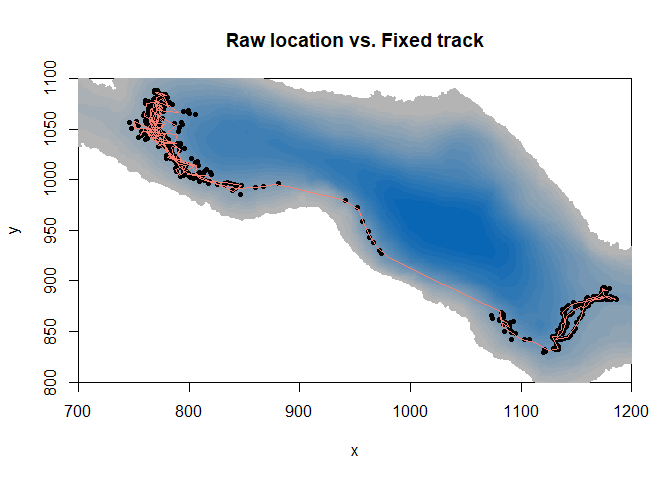
Ainsi, nous avons notre trajectoire observée. Maintenant, nous voulons simuler des trajectoires par une randomisation des pas effectués par les poissons. Mais nous voulons correspondre à la capacité de l’individu à faire face aux contraintes thermiques qu’il subit. Et nous ne voulons pas qu’il sorte du lac.
Ajouter une fonction de contrainte
Vérifier la profondeur minimale à laquelle le poisson s’est déplacé pour avoir une zone restreinte où des poissons aléatoires pourront également se déplacer
# Définir la profondeur minimale où le poisson est capable d'aller
lim_depth=min(fish$Depth,na.rm=T)
print(lim_depth)
## [1] 2.352525
# Créer un raster avec seulement les zones du lac avece ce minimum de profondeur
# Pour ce faire, j'ai inélégamment transformer le raster de bathymétrie en un tableau.
map_temp=as.data.frame(ledoux_depth, row.names=NULL, optional=FALSE, xy=TRUE,
na.rm=FALSE, long=FALSE)
# Puis j'ai sélectionner seulement les endroits du lac suffisamment profonds pour accueillir le poisson observé.
map_temp=map_temp[which(map_temp$layer>=lim_depth),]
# Je crée un raster vide des même dimensions que les raster original du lac
e <- extent(c(min(map_temp$x),max(map_temp$x),min(map_temp$y),max(map_temp$y)))
ncellx=(e[2]-e[1])
ncelly=(e[4]-e[3])
empty_r<- raster(e, ncol=ncellx, nrow=ncelly)
# Finalement j'intègre les endroits sélectionnés dans le raster vide
r <- rasterize(map_temp[, 1:2], empty_r, map_temp[,3], fun=mean)
# J'ai construit une fonction de contrainte qui doit avoir un objet de type SpatialPixelsDataFrame donc nous convertissons le raster
map <- as(r, "SpatialPixelsDataFrame")
crs(map)<-NA
# Ici, la zone du lac où nous allons autoriser la simulation de trajectoires, dépendamment de la distribution en profondeur du poisson observé
image(ledoux_depth,col="black",ylim=c(780,1150),xlim=c(300,1600))
par(new=T)
image(r,ylim=c(780,1150),col=palette,xlim=c(300,1600))
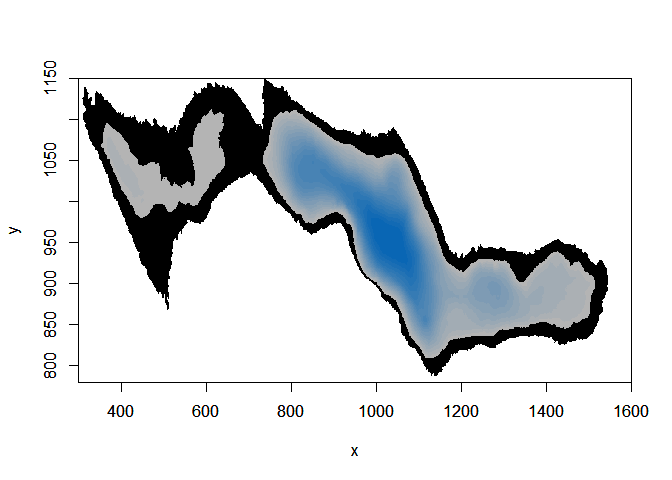
Ensuite, nous pouvons construire une fonction qui supprimera toutes les trajectoires simulées qui tombent en dehors de l’aire définie.
# fonction de contrainte qui supprime l'emplacement si les coordonnées d'une trajectoire simulée (x) tombaient en dehors de la zone contrainte (par). Cette fonction de contrainte est l'un des arguments intégrés à la fonction simulant les trajectoires.
consfun <- function(x, par){
coordinates(x) <- x[,1:2]
ov <- over(x, geometry(par))
return(all(!is.na(ov)))
}
Lancement de la création des trajectoires simulées
Tout d’abord, nous créons un modèle, en précisant si nous voulons ou non des angles ou des longueurs de pas aléatoires et si nous forçons les trajectoires simulées à commencer au début de la trajectoire observée. Nous devons également spécifier le nombre d’itérations que nous voulons faire.
mo <- NMs.randomCRW(na.omit(fixed_track), rangles=TRUE, rdist=TRUE,
constraint.func=consfun,
constraint.par = map, nrep=9,fixedStart=TRUE)
Ensuite, on doit faire tourner le modèle
Simulated_tracks=testNM(mo)
Regardons ces trajectoires simulées
# Transformer la liste des trajectoires en data frame, en ajoutant une colonne "no" pour l'id de la trajectoire ; 1 étant celui observé, et 2 à 10, les 9 simulations
no=1
RSF_database=cbind(fixed_track[[1]][,c(1,2)],no)
for (i in 1:9){
no=i+1
RSF_database=rbind(RSF_database,cbind(Simulated_tracks[[1]][[i]][,c(1,2)],no))
}
# Un vecteur de couleur pour avoir la trajectoire observée en couleur et les simulées en gris.
couleurs=c("salmon",gray.colors(9, start = 0.3, end = 0.9, gamma = 2.2, rev = FALSE))
# Représenter la carte
image(ledoux_depth,col=palette,ylim=c(780,1150),main="Simulated and observed trajectories")
#Ajouter toutes les lignes de trajectoire
for (i in 10:1){
temp=subset(RSF_database,no==i)
lines(temp$x,temp$y,col=couleurs[i])
}
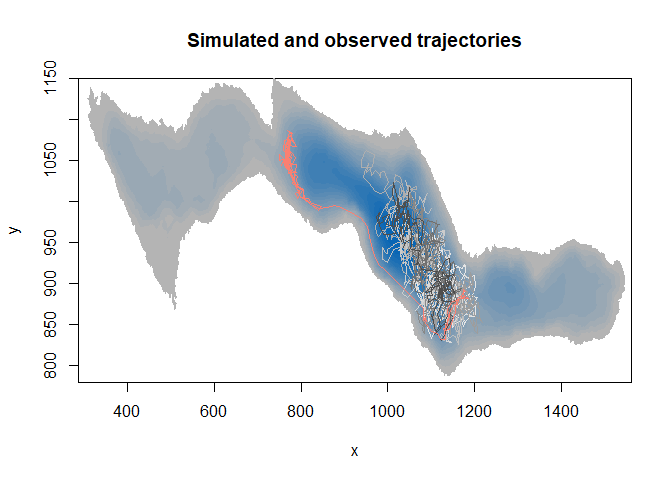
Innovation 3D
Maintenant, pour associer des données zooplanctoniques précises, nous devons savoir dans quelle couche se trouve nos poisson simulés. Pour ce faire, nous attribuons au hasard une profondeur pour chaque emplacement aléatoire, choisi à partir de la distribution réelle des poissons.
• Distribution en profondeur du poisson
distri_depth=fish$Depth
hist(distri_depth,main="",xlab="Depth (m)")
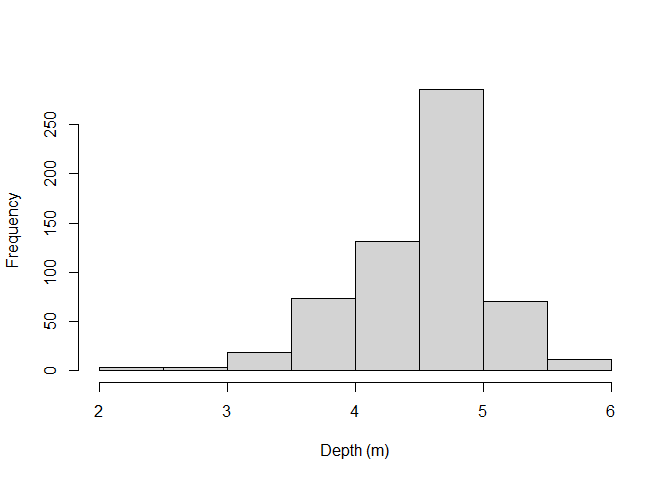
• Recalcul de la profondeur réelle pour la trajectoire observée Simplement, la profondeur pour la trajectoire observée (un pas par minute) a été interpolée à partir des mesures de profondeur aux emplacements d’origine encadrant les emplacements des pas
##Passons rapidement sur le recalcul de la profondeur réelle pour la trajectoire observée
fixed_track[[1]]$depth=NA
#Boucle for pour assigner une profondeur à chaque localisation dans la trajectoire observée
for (i in 1:nrow(fixed_track[[1]])){
# le temps à la localisation i
time_stamp=as.numeric(substr(fixed_track[[1]]$date[i],12,13))*3600+
as.numeric(substr(fixed_track[[1]]$date[i],15,16))*60+
as.numeric(substr(fixed_track[[1]]$date[i],18,19))
# Regrouper les temps de toutes les mesures de profondeur
time_table=as.numeric(substr(fish[,"posix_est"],12,13))*3600+
as.numeric(substr(fish[,"posix_est"],15,16))*60+
as.numeric(substr(fish[,"posix_est"],18,19))
# Selectionner la profondeur où le temps de la mesure est la plus proche du temps de la localisation i
ind_timing1=which(abs(time_stamp-time_table)==min(abs(time_stamp-time_table),na.rm=T))
print(c(i,length(ind_timing1)))
# Si les deux (précédent et suivant) mesures de profondeur sont disantes de manière égale dans le temps, on moyenne les profondeurs entre les deux pour avoir une profondeur à la localisation i
if(length(ind_timing1)==2){
fixed_track[[1]]$depth[i]=mean(fish[,"Depth"][ind_timing1])
}
# Si on a qu'une mesure de profondeur la plus proche
if(length(ind_timing1)==1){
# Si la mesure de profondeur la plus proche est après le temps de localistion i, on prend cette mesure et celle avant pour ensuite faire une interpolation linéaire pour retrouver la profondeur à la localisation i
if(time_stamp-time_table[ind_timing1]<0){
ind_timing2=ind_timing1-1
time=time_table[ind_timing1]-time_table[ind_timing2]
depth_var=fish[ind_timing1,"Depth"]-fish[ind_timing2,"Depth"]
depth_inter=(time_stamp-time_table[ind_timing2])*(depth_var/time)+fish[ind_timing2,"Depth"]
fixed_track[[1]]$depth[i]=depth_inter
}
# Si la mesure de profondeur la plus proche est avant le temps de localistion i, on prend cette mesure et celle après pour ensuite faire une interpolation linéaire pour retrouver la profondeur à la localisation i
if(time_stamp-time_table[ind_timing1]>0){
ind_timing2=ind_timing1+1
time=time_table[ind_timing2]-time_table[ind_timing1]
depth_var=fish[ind_timing2,"Depth"]-fish[ind_timing1,"Depth"]
depth_inter=(time_stamp-time_table[ind_timing1])*(depth_var/time)+fish[ind_timing1,"Depth"]
fixed_track[[1]]$depth[i]=depth_inter
}
# Si la mesure de profondeur la plus proche est au temps exact de la localisation i, on prend directement cette mesure pour assigner une profondeur à la localisation i
if(time_stamp-time_table[ind_timing1]==0){
fixed_track[[1]]$depth[i]=fish[ind_timing1,"Depth"]
}
}
}
• Assignement des profondeurs aux trajectoires simulées
Pour attribuer une profondeur aux trajectoires simulées, il est nécessaire de contrôler la profondeur de la colonne d’eau pour s’assurer que notre poisson aléatoire n’est pas dans le sol. Ensuite, échantillonnez simplement la distribution au hasard.
# Créer une colonne pour recevoir la profondeur de la colonne d'eau pour chaque localisation simulée
RSF_database$max_depth=NA
# Utilise la fonction extract du package raster pour récupérer la profondeur de la colonne d'eau pour chaque localisation simulée
RSF_database$max_depth=extract(ledoux_depth,RSF_database[,c(1:2)])
# Vecteur vide
depth_random=NA
#Boucle for où on colle chaque échantillonnage aléatoire de profondeur dans le vecteur
for (i in which(RSF_database$no!=1)){
depth_random=c(depth_random,sample(distri_depth[which(distri_depth<=RSF_database$max_depth[i])],1))
}
#Ensuite, dans la base de données regroupant toutes les trajectoires observée et simulées, on ajoute la colonne profondeur
RSF_database$depth=c(fixed_track[[1]]$depth,depth_random[-1])
#Voyons comment se comporte notre distribution en profondeur
ggplot(RSF_database,aes(x=depth))+
geom_histogram(position="dodge",bins=15)+
facet_wrap(~no)
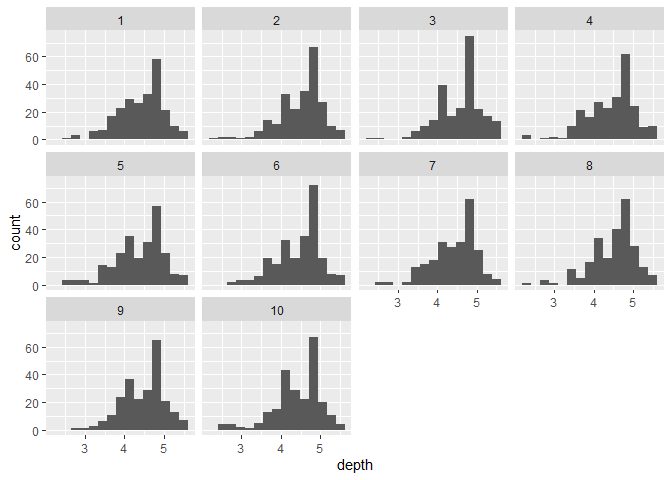
Histrogrammes des distributions de profondeurs pour chacune des trajectoires
Assigner mes valeurs des variables testée
Une fois que nous avons des emplacements 3D, nous pouvons ajouter les valeurs correspondantes des variables que nous voulons tester. Ici, on pourrait par exemple ajouter la valeur du biovolume de zooplancton supérieur à 1 mm rencontré à chaque endroit. C’est le même principe que pour extraire la profondeur maximale d’un raster mais on a autant de raster que de niveaux de profondeur différents (tous les mètres).
# Créer un vecteur d'intervalle de profondeur
depth_vector=seq(-0.5,16.5,1)
# Charger la base de données zooplancton
load("large_Z.Rdata")
# Créer la colonne avec les futures concentrations en zooplancton
RSF_database$LZ=NA
# Créer un raster vide pour créer un raster zooplancton qui sera extrait pour chaque couche de profondeur
e <- extent(ledoux_depth)
#Résolution horizontale souhaitée : 5m par 5m
ncellx=(e[2]-e[1])/5
ncelly=(e[4]-e[3])/5
r<- raster(e, ncol=ncellx, nrow=ncelly)
# Boucle for pour assigner les concentrations en zooplanction à la fois aux localisations simulées mais aussi observées, pour chaque couche de profondeur
for (prof in 1:(length(depth_vector)-1)){
# Sous-échantillon de la base de données trajectoires avec seulement les localisations dans la bonne couche de profondeur
temp=RSF_database[which(RSF_database$depth>=depth_vector[prof]&RSF_database$depth<depth_vector[prof+1]),]
# Si on a des localisations dans cette couche
if(nrow(temp)>0){
# Selection des mesures de zooplancton pour la couche correspondante
tempZ=Large_zooplankton[which(Large_zooplankton$Depth==(depth_vector[prof]+0.5)),c("X","Y","Predicted")]
# Transformer en un raster
temp_rast_LZ <- rasterize(tempZ[, 1:2], r, tempZ[,3], fun=mean)
# Extraire les concentrations de zooplancton pour toutes les localisations dans cette couche de profondeur
RSF_database$LZ[which(RSF_database$depth>=depth_vector[prof]&RSF_database$depth<depth_vector[prof+1])]=extract(temp_rast_LZ,RSF_database[which(RSF_database$depth>=depth_vector[prof]&RSF_database$depth<depth_vector[prof+1]),c(1,2)])
}
}
head(RSF_database)
## x y no max_depth depth LZ
## 1 1173.186 884.1521 1 6.024511 4.662200 0.7207559
## 2 1159.294 879.7437 1 6.263787 4.865985 0.7048485
## 3 1148.501 877.7077 1 7.330539 5.414200 0.6943779
## 4 1141.109 873.0767 1 7.961336 5.494100 0.7068840
## 5 1137.569 868.3407 1 8.414603 5.564600 0.4528299
## 6 1140.373 858.1783 1 7.483882 5.275326 0.7034004
Une fois toutes les variables attachées à la base de données RSF, nous avons presque terminé ! Il reste à pondérer les points disponibles par rapport à ceux utilisés (pour les explications, voir Fithian & Hastie 2013 ou Fieberg et al 2021). L’étape suivante consiste à exécuter une régression logistique conditionnelle avec la base de données pour enfin avoir nos coefficients de sélection.
RSF_database$weight=ifelse(RSF_database$no==1,1,5000)
Modèle RSF
Donc une RSF est juste une regression logistique conditionnelle, avec seulement quelques subtilités…
#Pour les régression conditionnelle, on a besoin d'une variable VRAI/FAUX. Ici, seule la trajectoire no°1 est VRAIE puisque c'est l'observée
RSF_database$case=RSF_database$no==1
# Mettre à l'échelle les variables
RSF_database$LZ=scale(RSF_database$LZ)
RSF_database$max_depth=scale(RSF_database$max_depth)
# Ecrire le modèle de régression
RSF_model= glm(case ~ max_depth + LZ,data = RSF_database,weight=weight, family = binomial(link = "logit"))
summary (RSF_model)
##
## Call:
## glm(formula = case ~ max_depth + LZ, family = binomial(link = "logit"),
## data = RSF_database, weights = weight)
##
## Deviance Residuals:
## Min 1Q Median 3Q Max
## -1.9921 -0.5242 -0.1607 -0.0488 4.7610
##
## Coefficients:
## Estimate Std. Error z value Pr(>|z|)
## (Intercept) -12.18314 0.17934 -67.932 < 2e-16 ***
## max_depth -2.39422 0.16294 -14.694 < 2e-16 ***
## LZ -0.46373 0.08337 -5.562 2.67e-08 ***
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
##
## (Dispersion parameter for binomial family taken to be 1)
##
## Null deviance: 5504.2 on 2342 degrees of freedom
## Residual deviance: 5041.4 on 2340 degrees of freedom
## (57 observations effacées parce que manquantes)
## AIC: 5047.4
##
## Number of Fisher Scoring iterations: 8
La profondeur de la colonne d’eau et la concentration de zooplancton sont sélectionnées négativement. Zooplancton évité ? À suivre… … Une fois que nous avons le coefficient, nous pouvons calculer la force de sélection des ressources (RSS) comme RSS=exp(coeff). RSS est la probabilité qu’un poisson soit trouvé dans une zone avec (xRSS) lorsque la valeur de cette variable augmente d’une unité.
RSS_zoo=exp(RSF_model$coefficients[3])
paste0("RSS = ",round(RSS_zoo,3))
## [1] "RSS = 0.629"
Attention toutefois au nombre de trajectoires simulées nécessaires et à la significativité du modèle !
Ces parties demandent beaucoup de temps de calcul (plusieurs jours pour un seul poisson) donc voici quelques validations déjà faites.
Controler combien de trajectoires simulées sont nécessaires
# Ici une base de données contenant des estimations de régression calculées 10 fois avec différents nombres de trajectoires simulées pour nos poissons
N_Simul=read.csv("S4_base.csv")
N_Simul_Z=N_Simul[which(N_Simul$param=="Large zooplankton"),]
ggplot(N_Simul_Z, aes(y=coeff,group=N_random_tracks))+
geom_boxplot(outlier.shape = NA)+
theme_bw()+
xlab("Number of simulated trajectories")+
scale_x_continuous(breaks=c(seq(-0.4,0.4,0.8/6)),
labels=as.character(seq(0,300,50)))+
geom_vline(xintercept=0,lty=2)+
theme(axis.title.x = element_text(size=14),axis.text.x = element_text(size=14),axis.text.y = element_text(size=14))+
theme(legend.position = "None")+
ylab(paste0("RSF estimate"))
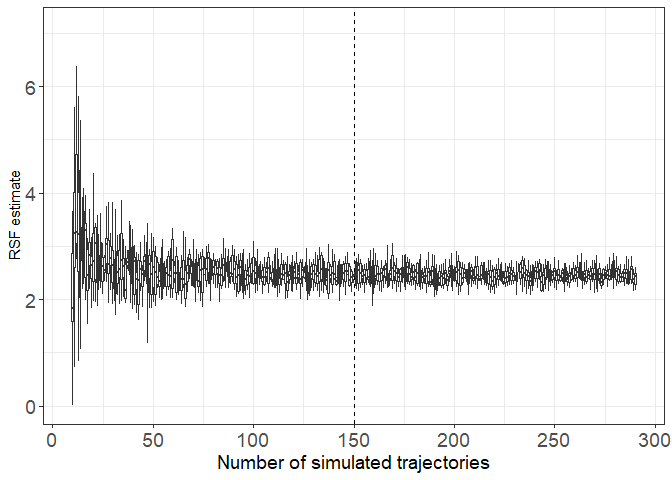
On constate ici une grande variabilité des estimations lorsque moins de 50 trajectoires simulées sont construites pour calculer le coefficient de la régression logistique. Pour être prudent, j’ai décidé de garder 150 trajectoires simulées pour être sûr d’avoir une estimation de coefficient stable.
Contrôle pour la valeur de p
Étant donné que notre régression est basée sur des milliers de points, la taille de l’échantillon pourrait induire une significativité automatique de la valeur de p. Pour éviter ce biais, nous avons construit la distribution des estimations sous l’hypothèse nulle. Cela signifie que le coefficient de régression que nous calculons doit être supérieur ou inférieur à au moins 95 % des estimations qui seraient calculées à partir d’une comparaison d’une trajectoire simulée avec 150 autres trajectoires simulées.
# Impoter la base de données où nous avons calculé 500 fois la régression basée sur une trajectoire simulée et 150 autres trajectoires simulées
H0_500=read.csv("HO_500.csv")
# Impoter la base de données où nous avons calculé un nombre de fois variable la régression basée sur une trajectoire simulée et 150 autres trajectoires simulées
H0_data= read.csv("S5DB.csv",row.names=1)
ggplot(H0_500, aes(x=RSF_estimate))+
geom_histogram(fill="gray80",colour="gray50",bins=18,aes(y=(..count../sum(..count..)) * 100))+
theme_bw()+
geom_vline(xintercept = quantile(H0_500$RSF_estimate,c(0.025,0.975)),lty=2)+
xlab("RSF estimate")+
theme(axis.title.y = element_text(size=14),axis.title.x = element_text(size=14),axis.text.x = element_text(size=14),axis.text.y = element_text(size=14))+
theme(legend.position = "None")+
ylab(paste0("Percentage of occurrence (%)"))
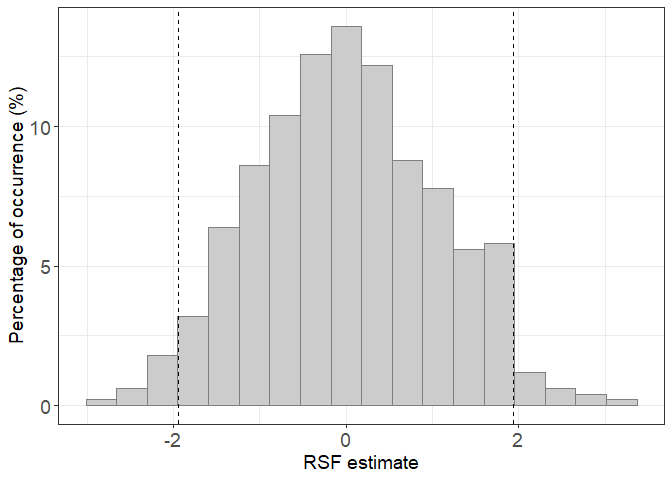
Lorsque nous calculons la RSF pour le poisson, le coefficient doit être en dehors de la plage [-2;2] pour être considéré comme différent de 0 (c’est-à-dire pour montrer une sélection active ou un évitement). Ici, la distribution est tracée après répétition de 500 H0 RSF. Mais ce nombre doit être évalué au préalable pour être sûr qu’il est suffisant pour construire la distribution H0.
ggplot(H0_data, aes(y=inf,x=N_H0_RSF))+
geom_smooth(col="gray50")+
geom_smooth(aes(y=sup,x=N_H0_RSF),col="gray50")+
geom_point()+
geom_point(aes(y=sup,x=N_H0_RSF))+
theme_bw()+
geom_vline(xintercept = 500,lty=2)+
xlab("Number of RSF iterations")+
theme(axis.title.y = element_text(size=14),axis.title.x = element_text(size=14),axis.text.x = element_text(size=14),axis.text.y = element_text(size=14))+
theme(legend.position = "None")+
ylab(paste0("Boundaries of the 5% confidence interval of RSF estimates"))
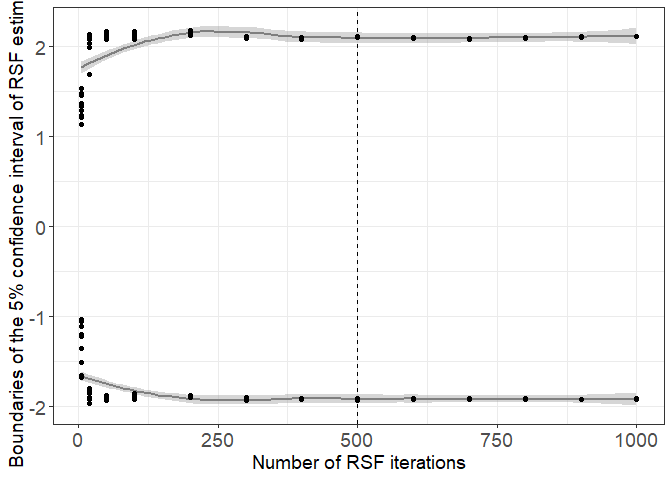
On voit qu’avec plus de 400 itérations, l’intervalle de confiance à 95% est stable. Nous avons choisi 500 itérations pour être prudent.
Post-analyses et interprétations rapides
Voyons quelques résultats réels, en termes d’occurrences de sélection, d’intensités et d’interactions. (Leroux et al. en préparation)
Bibliographie
Bertolo, A., Pépino, M., Adams, J., & Magnan, P. (2011). Behavioural thermoregulatory tactics in lacustrine brook charr, Salvelinus fontinalis. PLoS One, 6(4), e18603.
Bourke, P., Magnan, P., & Rodriguez, M. A. (1996). Diel locomotor activity of brook charr, as determined by radiotelemetry. Journal of Fish Biology, 49(6), 1174-1185.
Bourke, P., Magnan, P., & Rodríguez, M. A. (1999). Phenotypic responses of lacustrine brook charr in relation to the intensity of interspecific competition. Evolutionary Ecology, 13(1), 19-31.
Boyce, M. S., & McDonald, L. L. (1999). Relating populations to habitats using resource selection functions. Trends in ecology & evolution, 14(7), 268-272.
Calenge, C. (2011). Analysis of animal movements in R: the adehabitatLT package. R Foundation for Statistical Computing, Vienna.
Fieberg, J., Signer, J., Smith, B., & Avgar, T. (2021). A ‘How to’guide for interpreting parameters in habitat‐selection analyses. Journal of Animal Ecology, 90(5), 1027-1043.
Fithian, W., & Hastie, T. (2013). Finite-sample equivalence in statistical models for presence-only data. The annals of applied statistics, 7(4), 1917.
Goyer, K., Bertolo, A., Pépino, M., & Magnan, P. (2014). Effects of lake warming on behavioural thermoregulatory tactics in a cold-water stenothermic fish. PLoS One, 9(3), e92514.
Magnan, P. (1988). Interactions between brook charr, Salvelinus fontinalis, and nonsalmonid species: ecological shift, morphological shift, and their impact on zooplankton communities. Canadian Journal of Fisheries and Aquatic Sciences, 45(6), 999-1009.
Munden, R., Börger, L., Wilson, R. P., Redcliffe, J., Brown, R., Garel, M., & Potts, J. R. (2021). Why did the animal turn? Time‐varying step selection analysis for inference between observed turning‐points in high frequency data. Methods in Ecology and Evolution, 12(5), 921-932.
Thurfjell, H., Ciuti, S., & Boyce, M. S. (2014). Applications of step-selection functions in ecology and conservation. Movement ecology, 2(1), 1-12.