Transition douce à l’approche bayésienne

Charles Martin

Septembre 2025

Introduction

Si vous êtes comme moi, les statistiques bayésiennes vous ont probablement toujours paru comme un idéal. Quelque chose que les autres font, pas vous. Eux, les vrais statisticiens!

Le but de cet atelier est de déconstruire ce mythe. De vous montrer qu’en 2025, cette approche est non seulement accessible, mais aussi plus facile à interpréter, plus directe. Elle est en fait tout ce que vous auriez toujours voulu que vos statistiques soient! Nous réussiront même à l’approcher sans équation mathématique comme tel!

L’approche fréquentiste des statistiques, i.e. celle que l’on vous a enseignée jusqu’à ce jour, est fondée sur le principe qu’il existe une “vraie” valeur fixe, la valeur de la population, pour chacun des paramètres que vous voulez estimer. L’approche fréquentiste vous fournit ensuite une série d’outils (test de T, ANOVA, etc.) qui sont conçus pour que, sur le long terme, si on les utilise un nombre très élevé de fois, leurs propriétés statistiques (valeur de p, intervalle de confiance) se réalisent.

Du point de vue bayésien, l’incertitude dans nos estimations, les probabilités comme tel, sont une conséquence de notre incapacité à tout mesurer en détail. L’incertitude est notre outil, pour évaluer tout ce que l’on ne comprend pas ou ne pouvons pas mesurer d’un système. Les données sont donc considérées comme réelles, précises : c’est ce que nous avons mesuré. Les paramètres, au contraire, sont l’objet de l’incertitude. On ne peut pas connaître précisément le phénomène, parce que l’on ne peut pas tout mesurer.

L’autre aspect fondamental de l’approche bayésienne est que cette dernière est conçue comme un processus de mise à jour de nos connaissances. Avant l’expérience, nous avons une certaine quantité d’information, de certitudes. Nous récoltons ensuite des données, qui nous permettent de mettre à jour nos connaissances sur le phénomène à l’étude. Cet aspect est à la fois le plus puissant, mais aussi le plus polarisant de l’approche bayésienne, puisqu’il permet, si on le désire, d’insérer une certaine subjectivité dans le processus.

D’un côté certains dirons que cette subjectivité n’a pas sa place en science, et que l’on devrait regarder chaque expérience en vase clos. Mais beaucoup vous dirons qu’aujourd’hui, une grande partie des problèmes de réplication auxquels fait face la science moderne auraient pu être évités si l’analyse des hypothèses les plus farfelues (ou innovatrices!) avait débuté avec a priori très peu de probabilités que l’hypothèse soit vraie.

Révision de l’approche fréquentiste

Avant de nous lancer dans l’approche bayésienne, prenons quelques instants pour réviser l’approche fréquentiste. Nous tenterons ici de répondre à la question : qu’est-ce qui influence le poids de manchots de l’archipel de Palmer? Parmi les phénomènes d’intérêt, nous avons mesuré la longueur des ailes (mm, capacité de nage), la longueur du bec (mm, taille des proies), le sexe et l’espèce de chaque individu. Nous tenterons de voir comment ces variables influencent le poids des oiseaux (g).

Donc, commençons par charger les librairies nécessaires, soit le tidyverse pour la manipulation des données et la visualisation, et palmerpenguins pour les données comme tel.

library(tidyverse)
library(palmerpenguins)

Préparons ensuite un petit tableau de données qui nous suivra tout au long de l’exercice :

manchots <- penguins |> 
  select(body_mass_g, flipper_length_mm, bill_length_mm, sex, species) |> 
  drop_na()

Remarquez au passage que l’approche bayésienne serait tout à fait appropriée pour faire l’imputation de ces données manquantes plutôt que de simplement les éliminer, mais c’est un sujet pour un autre jour…

Ensuite, à l’aide de la fonction lm, ajustons un modèle de régression multiple qui tentera de répondre à notre question :

m <- lm(
  body_mass_g ~ 
    flipper_length_mm + bill_length_mm + sex + species, 
  data = manchots
)

summary(m)

Call:
lm(formula = body_mass_g ~ flipper_length_mm + bill_length_mm + 
    sex + species, data = manchots)

Residuals:
    Min      1Q  Median      3Q     Max 
-718.50 -201.60  -12.75  198.45  878.24 

Coefficients:
                  Estimate Std. Error t value Pr(>|t|)    
(Intercept)       -759.064    541.377  -1.402 0.161834    
flipper_length_mm   17.847      2.902   6.150 2.25e-09 ***
bill_length_mm      21.633      7.148   3.027 0.002670 ** 
sexmale            465.395     43.081  10.803  < 2e-16 ***
speciesChinstrap  -291.711     81.502  -3.579 0.000397 ***
speciesGentoo      707.028     94.359   7.493 6.35e-13 ***
---
Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1

Residual standard error: 292 on 327 degrees of freedom
Multiple R-squared:  0.8705,    Adjusted R-squared:  0.8685 
F-statistic: 439.7 on 5 and 327 DF,  p-value: < 2.2e-16

confint(m)

                         2.5 %     97.5 %
(Intercept)       -1824.084819  305.95606
flipper_length_mm    12.138156   23.55487
bill_length_mm        7.571439   35.69361
sexmale             380.644608  550.14539
speciesChinstrap   -452.044957 -131.37631
speciesGentoo       521.400228  892.65574

Donc, en gros, le poids des manchots augmente avec la longueur des ailes et avec la taille du bec, les mâles sont plus lourds que les femelles, et les manchots Chinstrap et Gentoo sont respectivement plus légers et plus lourds que les Adelie (le niveau de référence).

Là où les choses se compliquent est lorsqu’on s’intéresse au détail des statistiques. Par exemple, essayez de me nommer, sans fouiller sur internet, la définition fréquentiste d’un intervalle de confiance!

(pause)

Il s’agit d’un intervalle de valeurs qui, si on répète l’échantillonnage plusieurs fois dans les mêmes conditions, contiendra la vraie valeur de la population un certain pourcentage de fois (p. ex. 95%).

Pour l’effet de la longueur des ailes, l’intervalle est entre 12.14 et 23.55 g par mm d’aile. On voudrait pouvoir dire qu’il y a 95% des chances que la vraie valeur de la population soit entre ces bornes, mais rien dans l’approche fréquentiste ne permet de le faire. Cette philosophie assume que la valeur de la population est fixe, et par la suite, elle quantifie l’erreur produite par le processus d’échantillonnage. L’interprétation que l’on en fait couramment (95% des chances que la vraie valeur soit dans l’intervalle) est une interprétation purement bayésienne de la réalité.

L’autre statistique qui est couramment interprétée dans ces sorties est la valeur de p. Encore une fois, pouvez-vous me citer de mémoire la définition précise d’une valeur de p?

(pause)

La valeur de p est la probabilité d’observer des données au moins aussi extrêmes que celles trouvées si l’hypothèse nulle est vraie (ici que le paramètre soit exactement zéro).

Si on travaille dans un cadre fréquentiste, nos seuls outils d’inférence sont un intervalle de confiance, basé sur le long terme qui ne nous informe en rien sur les données actuelles et une valeur de p qui nous informe de la probabilité de trouver des données, hypothétiques, plus extrêmes que celles trouvées si une hypothèse farfelue est vraie (i.e. l’effet est d’exactement zéro).

Voyons maintenant comment les choses pourraient se dérouler avec l’approche bayésienne.

La version bayésienne

La première chose à savoir est qu’il existe maintenant plusieurs librairies R facilitant beaucoup les analyses les plus communes en mode bayésien. La librairie rstanarm est un excellent point de départ puisqu’elle contient des équivalents pour les fonctions de modélisation les plus connues comme stan_lm, stan_aov, stan_glm, stan_glmer, stan_nlmer et stan_gamm4. De plus, ses modèles sont pré-compilés, ce qui les rends presque aussi rapides que les versions fréquentistes. Dans la majorité des cas, on parle d’à peine quelques secondes de différence.

Donc, chargeons cette librairie, et ensuite, permettons lui d’utiliser plusieurs cœurs sur notre ordinateur, pour accélérer les traitement qui peuvent être faits en parallèle.

library(rstanarm)

Loading required package: Rcpp

This is rstanarm version 2.32.1

- See https://mc-stan.org/rstanarm/articles/priors for changes to default priors!

- Default priors may change, so it's safest to specify priors, even if equivalent to the defaults.

- For execution on a local, multicore CPU with excess RAM we recommend calling

  options(mc.cores = parallel::detectCores())

options(mc.cores = parallel::detectCores()-1)

Remarquez que je me réserve un cœur (-1) pour que mon ordinateur demeure bien utilisable pendant les traitements. Si ce n’est pas une priorité pour vous, vous pouvez lui laisser utiliser tous les cœurs.

Afin de désamorcer toute tension, voici immédiatement le même modèle, analysé dans un cadre bayésien :

m_bayes <- stan_glm(
  body_mass_g ~ 
    flipper_length_mm + bill_length_mm + sex + species, 
  data = manchots
)

summary(m_bayes)

Model Info:
 function:     stan_glm
 family:       gaussian [identity]
 formula:      body_mass_g ~ flipper_length_mm + bill_length_mm + sex + species
 algorithm:    sampling
 sample:       4000 (posterior sample size)
 priors:       see help('prior_summary')
 observations: 333
 predictors:   6

Estimates:
                    mean    sd      10%     50%     90%  
(Intercept)        -748.7   548.4 -1451.0  -752.9   -53.7
flipper_length_mm    17.8     3.0    14.0    17.8    21.6
bill_length_mm       21.4     7.2    12.2    21.2    30.5
sexmale             466.3    42.9   411.4   466.0   520.9
speciesChinstrap   -289.3    82.0  -393.5  -288.7  -185.8
speciesGentoo       709.0    95.2   590.8   707.3   829.6
sigma               293.0    11.2   278.9   292.7   307.3

Fit Diagnostics:
           mean   sd     10%    50%    90% 
mean_PPD 4206.9   22.9 4177.9 4206.9 4236.7

The mean_ppd is the sample average posterior predictive distribution of the outcome variable (for details see help('summary.stanreg')).

MCMC diagnostics
                  mcse Rhat n_eff
(Intercept)       12.2  1.0 2006 
flipper_length_mm  0.1  1.0 2505 
bill_length_mm     0.2  1.0 1963 
sexmale            0.9  1.0 2086 
speciesChinstrap   1.9  1.0 1840 
speciesGentoo      2.3  1.0 1653 
sigma              0.2  1.0 3246 
mean_PPD           0.4  1.0 3875 
log-posterior      0.0  1.0 1695 

For each parameter, mcse is Monte Carlo standard error, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence Rhat=1).

posterior_interval(m_bayes)

                            5%        95%
(Intercept)       -1654.022655  143.67009
flipper_length_mm    13.005745   22.79919
bill_length_mm        9.675732   33.06481
sexmale             398.062553  537.16807
speciesChinstrap   -419.471533 -156.80500
speciesGentoo       554.227684  864.33638
sigma               275.195951  311.73817

C’est tout, vous avez roulé votre premier modèle bayésien! Tout est identique à 4 caractères près (stan_)

Remarquez d’abord la première chose rassurante : les estimés de paramètres moyens sont essentiellement identiques à ceux produits par lm . Entre autres, l’effet de la longueur des ailes est de 17.83 g/mm vs 17.85 g/mm, les mâles sont 466.02 g plus lourds que les femelles vs. 465.4 dans l’approche fréquentiste, etc.

Vos chiffres pour l’approche bayésienne pourraient être légèrement différents des miens, ce qui est tout à fait normal puisqu’il s’agit d’un processus d’échantillonnage aléatoire.

Le premier avantage de l’approche bayésienne est que l’on peut directement interpréter l’incertitude associée aux paramètres. Par exemple, l’intervalle de crédibilité à 95% de l’effet de la longueur des ailes va de 13.01 et 22.8 g/mm. Donc, ici, on est en droit de dire qu’il y a 95% des chances que la vraie valeur du paramètre soit entre ces deux bornes! Pas de définition compliquée, rien à propos d’échantillons hypothétiques non-récoltés. C’est tout : 95% des chances que le vrai effet de la longueur des ailes soit entre 13.01 et 22.8 g/mm.

La méthode de Monte-Carlo par chaîne de Markov (MCMC)

Après ce petit tour de magie, il est évidemment utile d’expliquer comment stan_glm est arrivé à ces chiffres.

Vous savez peut-être qu’il existe plusieurs façons d’arriver aux meilleures valeurs pour les paramètres dans un modèle statistique.

La fonction lm utilise une petite séquence d’algèbre matriciel pour produire des paramètres qui minimiserons toujours la somme des carrés des résidus.

Dans les cas plus complexes comme des GLM ou des modèles mixtes, l’approche classique est plutôt de maximiser la vraisemblance du modèle. Autrement dit, de trouver les valeurs des paramètres les plus probables connaissant les données. Dans ce cas, l’algorithme démarre d’une solution aléatoire, et se déplace à travers le paysage de vraisemblance pour tenter de trouver la combinaison de valeurs la plus probable. Si vous avez par le passé reçu des messages d’erreur de non-convergence, c’est que cet algorithme n’a pas réussi à se stabiliser à un endroit. Il oscille sans réussir à déterminer la meilleure combinaison.

Dans ces deux paradigmes, l’incertitude autour des paramètres est ensuite estimée à partir de la matrice de variance/covariance, avec l’assomption que cette incertitude suit une distribution normale, symétrique, autour du paramètre.

L’approche bayésienne est bien différente. Tout d’abord, son exploration du paysage de vraisemblance est basée sur la méthode de Monte-Carlo par chaînes de Markov (MCMC, Markov Chain Monte Carlo). À elle seule, cette technique mériterait son propre atelier Numérilab, mais l’idée principale est la suivante : à partir d’un endroit dans le paysage, la chaîne de Markov détermine aléatoirement une destination, et plus cette destination est probable, plus elle a de chances d’être explorée. Si l’algorithme décide d’explorer ce point, la probabilité d’observer les données à cet endroit est évaluée, puis elle sert de base pour le prochain saut. La conséquence principale de cette façon de faire est que, plus un endroit dans le paysage est probable, plus il sera exploré souvent.

Plusieurs algorithmes ont été proposés pour effectuer cette exploration, entre autres l’algorithme de Metropolis-Hasting, puis celui l’échantillonnage de Gibbs. Mais à l’heure actuelle, LA façon de faire est l’algorithme NUTS (No U-Turn Sampling), une variante de la méthode Hamiltonienne, implémentée dans le language de programmation spécialisé Stan.

Derrière le rideau, rstanarm utilise d’ailleurs ce langage de programmation pour ajuster vos modèles. Il traduit simplement vos formules et votre définition de données dans un format compréhensible à Stan, pour ensuite exécuter ce code et récupérer les résultats.

Outre la méthode pour parcourir le paysage, l’autre différence principale est que la méthode MCMC, plutôt que de conserver uniquement la destination finale, conservera chaque étape de l’exploration. Et comme la MCMC explore plus densément les endroits les plus probables, la distribution des valeurs explorées par la chaîne nous donnera directement la distribution des probabilités des valeurs qu’un paramètre pourrait prendre.

Chaque étape d’exploration est appelée un échantillon (draw) de la chaîne de Markov, et est contenue dans l’objet de résultats. Ces échantillons sont déjà présents dans l’objet m_bayes. Il suffit de le convertir en tableau de données pour procéder :

echantillons <- m_bayes |> 
  as.data.frame() |> 
  janitor::clean_names()
head(echantillons)

   intercept flipper_length_mm bill_length_mm  sexmale species_chinstrap
1  -573.9174          18.19149       15.80594 513.3798        -260.31328
2  -252.0096          16.18211       14.70172 504.1950         -83.48346
3  -946.1192          20.33267       14.45615 469.2250        -348.38158
4 -1186.0073          21.24113       16.56292 429.0112        -200.26425
5 -1083.4718          21.18507       13.98476 472.1859        -273.30921
6  -792.4604          17.09607       25.01554 490.7692        -352.07856
  species_gentoo    sigma
1       712.2061 287.3187
2       814.0626 301.1339
3       664.2254 293.7002
4       612.2247 289.5670
5       649.7714 271.0587
6       714.5493 280.2691

Remarquez que j’utilise aussi la fonction clean_names pour nous débarasser des parenthèses autour du mot “(Intercept)”.

On peut ensuite visualiser ou mesurer l’incertitude autour d’un paramètre :

echantillons |> 
  ggplot(aes(flipper_length_mm)) +
  geom_histogram()

`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.


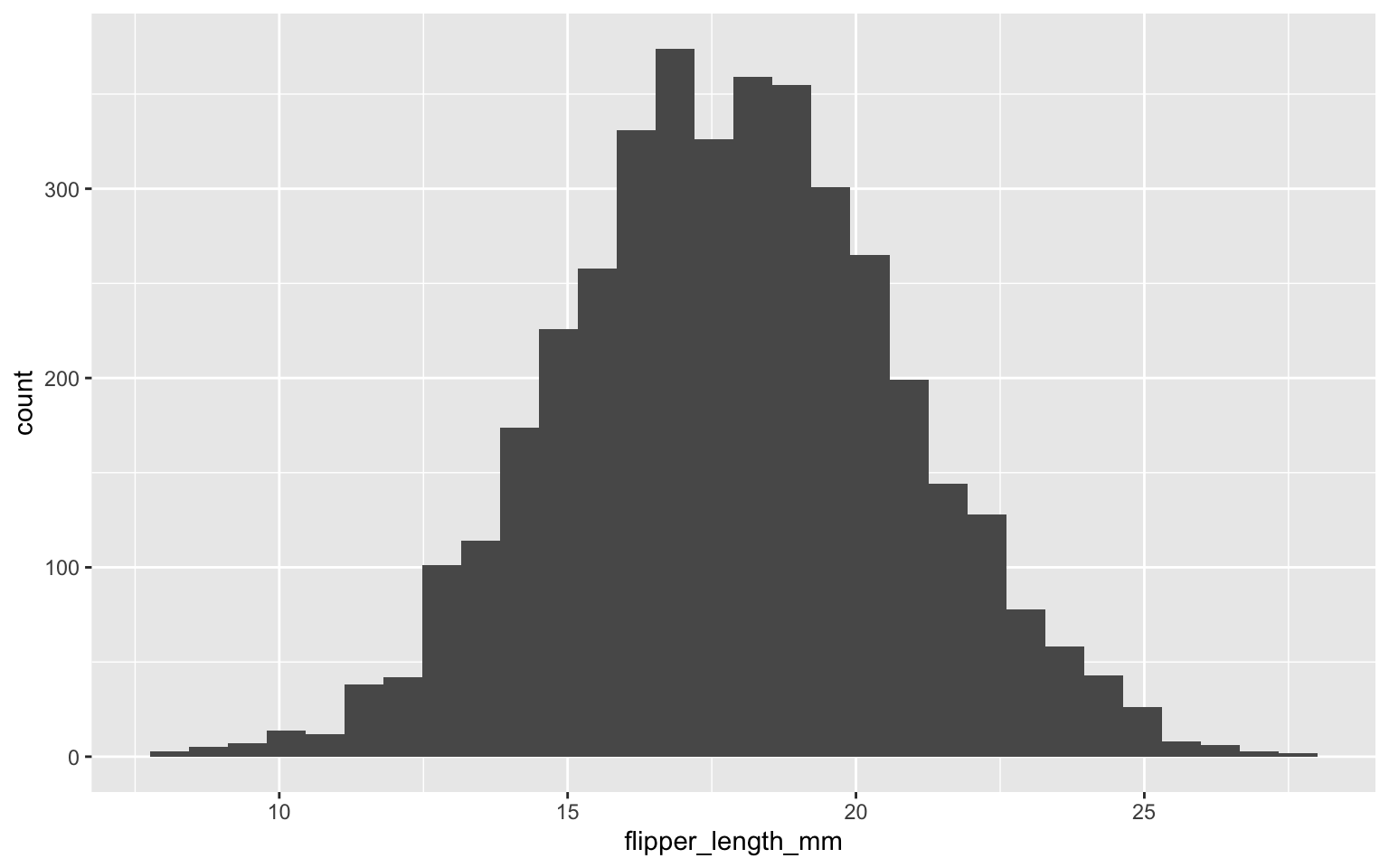
summary(echantillons$flipper_length_mm)

   Min. 1st Qu.  Median    Mean 3rd Qu.    Max. 
  8.174  15.875  17.831  17.845  19.809  27.741

Donc, l’algorithme a convergé autour de la valeur de 17.84 ou 17.83 selon que l’on se fie à la moyenne ou à la médiane des échantillons. Visuellement, on peut rapidement constater que décrire l’incertitude autour de ce paramètre à l’aide de l’écart-type sera tout à fait approprié, puisque les échantillons suivent une belle courbe normale.

On peut aussi calculer directement toutes les probabilités qui nous intéressent, par exemple la probabilité que l’effet de la longueur des ailes soit plus grand que 20 g/mm :

sum(echantillons$flipper_length_mm>20)/length(echantillons$flipper_length_mm)

[1] 0.23125

Par contre, ce n’est pas obligatoire que l’incertitude soit symétrique. Par exemple, celle autour du paramètre d’erreur, est plutôt asymétrique :

echantillons |> 
  ggplot(aes(sigma)) +
  geom_histogram()

`stat_bin()` using `bins = 30`. Pick better value with `binwidth`.

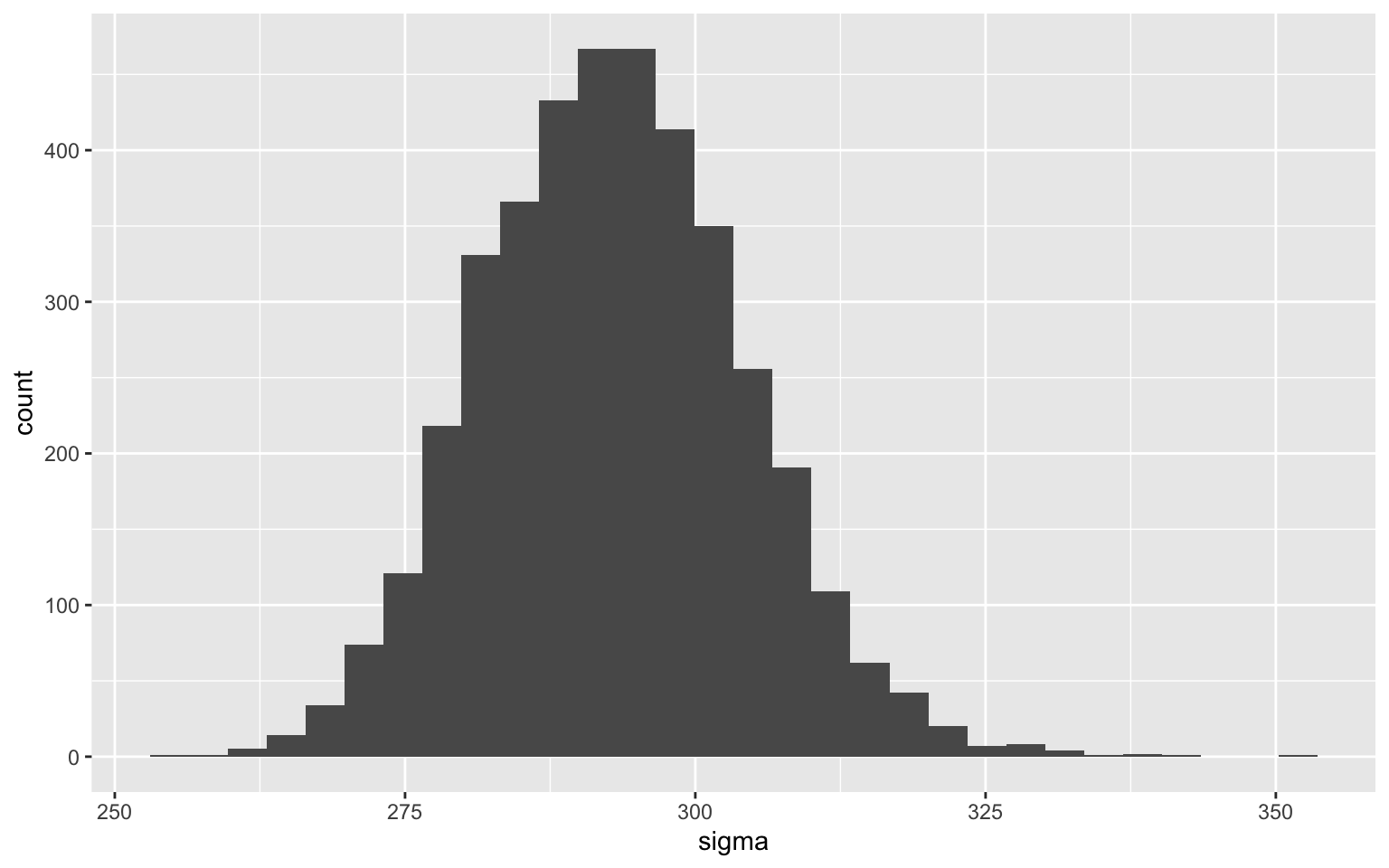
Ce qui est tout à fait normal, si on réfléchit au fait que le paramètre est un terme de variance dans le modèle et que la variance ne peut jamais être négative.

Comme nous avons tous les échantillons et que nous ne prenons pas de raccourcis pour estimer l’incertitude, on peut directement évaluer cette asymétrie :

quantile(echantillons$sigma, probs = c(0.015,.5,.985))

    1.5%      50%    98.5% 
270.1696 292.7012 317.9939

La médiane du paramètre est à environ 293, mais les bornes de l’intervalle de crédibilité à 97% sont 24 plus bas et 26 plus haut que la médiane.

Comme vous voyez, tant qu’à vous défaire du cadre arbitraire de l’approche par tests d’hypothèses, vous pouvez aussi laisser tomber la valeur arbitraire de 95% pour les intervalles de confiance, qui n’a aucun fondement ou bienfaits théoriques. Vos intervalles sont tout aussi valides si elles sont des intervalles à 88 ou 92%.

Ce qui nous amène à une différence philosophique majeure. Contrairement à l’approche fréquentiste, l’approche bayésienne n’a pas à se prononcer sur la distribution des résidus ou sur leur homogénéité avant d’interpréter les paramètres d’un modèle. Les paramètres sont ce qu’ils sont et on peut toujours les interpréter comme tel (à condition que le processus MCMC ce soit déroulé correctement, nous y reviendrons).

Attention, il ne faut cependant pas faire de raccourcis non plus. On ne sait PAS si la longueur des ailes affecte vraiment le poids des manchots de façon linéaire au rythme de 17.8 mm/g. Aucun modèle ne permet de savoir cela. Ce que l’on sait, c’est que SI on ajuste un modèle linéaire pour le faire, on mesure une augmentation médiane de 17.8 mm/g.

Et c’est là toute la nuance. Il est quand même important d’observer les résidus du modèle pour voir si ce dernier est bien ajusté aux données, si il est approprié à la forme des relations, etc. Mais des déviations à cette étape ne rendent pas le modèle ininterprétable. Ils sont plutôt un indice que le modèle pourrait être amélioré. Une étape dans le processus itératif.

Intégrer l’information connue a priori

Nous avons jusqu’à maintenant évité le sujet, mais nous ne pourrons pas continuer bien longtemps sans en parler. Un des apports majeurs de l’approche bayésienne est qu’elle permet d’intégrer au calcul l’information connue a priori, avant de lancer la collecte de données. Elle est directement conçue comme un processus de mise à jour des connaissances, plutôt que de considérer chaque expérience comme indépendante.

La distribution de probabilité associée à un paramètre que nous avons vue ci-haut est en fait la probabilité a posteriori. La version mise à jour, après avoir confronté nos connaissances préalables aux nouvelles données recueillies. C’est ici qu’en général, les tutoriels sur l’approche bayésienne présentent le théorème de Bayes, et son application par exemple à des tests médicaux ou au dopage, en tenant compte des faux positifs, du taux de base dans la population, etc. Tout cela est bien intéressant, mais absolument pas nécessaire pour débuter avec cette approche.

L’important est surtout de comprendre, je le répète, que les résultats obtenus sont une mise à jour des connaissances a priori par les données recueillies.

Mais quelles informations a priori utiliser? Il existe pour cela plusieurs écoles de pensée

Les a priori non-informatifs

Une des choses les plus rassurantes lorsque l’on débute avec cette approche est de savoir qu’il est possible d’utiliser des a priori tellement vagues qu’ils n’ont aucun impact sur le résultat. Avec cette philosophie, nos résultats sont (dans les cas simples) identiques à ceux retrouvés par l’approche par vraisemblance maximale (p. ex. la fonction glm ou nlme dans R), à la différence que

  1. ils peuvent être interprétés dans un cadre bayésien et
  2. nous avons accès à tous les échantillons de la distribution postérieure pour observer la distribution des paramètres, leurs corrélations, etc.

Dans stan_glm, on aurait pu appliquer des a priori non-informatifs, par exemple, en mentionnant que pour ce que l’on en sait, les paramètres peuvent être ASBOLUMENT N’IMPORTE QUOI. Ils pourraient aller de -Inf à +Inf avec autant de probabilités pour chacune des valeurs.

m_noninformatif <- stan_glm(
  body_mass_g ~ 
    flipper_length_mm + bill_length_mm + sex + species, 
  data = manchots,
  prior = NULL,
  prior_intercept = NULL,
  prior_aux = NULL
)

summary(m_noninformatif)

Model Info:
 function:     stan_glm
 family:       gaussian [identity]
 formula:      body_mass_g ~ flipper_length_mm + bill_length_mm + sex + species
 algorithm:    sampling
 sample:       4000 (posterior sample size)
 priors:       see help('prior_summary')
 observations: 333
 predictors:   6

Estimates:
                    mean    sd      10%     50%     90%  
(Intercept)        -776.7   547.0 -1475.6  -778.7   -79.3
flipper_length_mm    17.9     2.9    14.2    18.0    21.6
bill_length_mm       21.8     7.2    12.6    21.8    31.0
sexmale             464.4    43.8   407.2   465.3   519.7
speciesChinstrap   -294.1    82.4  -398.5  -295.4  -186.1
speciesGentoo       704.0    95.4   579.0   704.7   827.2
sigma               293.2    11.5   278.7   292.8   307.9

Fit Diagnostics:
           mean   sd     10%    50%    90% 
mean_PPD 4207.1   22.9 4178.2 4207.2 4236.5

The mean_ppd is the sample average posterior predictive distribution of the outcome variable (for details see help('summary.stanreg')).

MCMC diagnostics
                  mcse Rhat n_eff
(Intercept)       12.5  1.0 1930 
flipper_length_mm  0.1  1.0 2276 
bill_length_mm     0.2  1.0 2126 
sexmale            0.9  1.0 2270 
speciesChinstrap   1.8  1.0 2080 
speciesGentoo      2.3  1.0 1769 
sigma              0.2  1.0 3267 
mean_PPD           0.4  1.0 3760 
log-posterior      0.0  1.0 1566 

For each parameter, mcse is Monte Carlo standard error, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence Rhat=1).

Comme prévu, ces résultats sont quasi-identiques à ceux obtenus par l’approche fréquentiste. ET aussi très proches de ceux obtenus avec les valeurs par défaut, dont nous discuterons plus bas.

Les a priori informatifs

À l’autre extrémité du spectre des a priori, on pourrait vouloir intégrer précisément notre connaissance du sujet avant de commencer l’expérience.

Afin de simplifier cette section, nous travaillerons sur une régression simple comportant un seul paramètre. La syntaxe pour modifier l’a priori d’un seul paramètre tout en gardant les autres valeurs par défaut n’est pas très conviviale dans stan_glm.

Si par exemple une étude exploratoire sur 20 manchots avait trouvé que l’effet de longueur des ailes était de 25 g/mm avec une erreur-type de 10 g/mm, on aurait pu intégrer cette information comme ceci :

m_informatif_20 <- stan_glm(
  body_mass_g ~ flipper_length_mm, 
  data = manchots,
  prior = normal(location = 25,scale = 10)
)

Nous comparerons maintenant ce modèle à un où nous utilisons un a priori non-informatif sur cette pente :

m_informatif_0 <- stan_glm(
  body_mass_g ~ flipper_length_mm, 
  data = manchots,
  prior = NULL
)

Et un où nous avons beaucoup de certitude avant de commencer le projet. On pourrait par exemple avoir mesuré 10 000 manchots et avoir trouvé une moyenne de 25, mais avec une erreur-type de +/- 1 g/mm

m_informatif_10000 <- stan_glm(
  body_mass_g ~ flipper_length_mm, 
  data = manchots,
  prior = normal(location = 25,scale = 1)
)

summary(m_informatif_0)

Model Info:
 function:     stan_glm
 family:       gaussian [identity]
 formula:      body_mass_g ~ flipper_length_mm
 algorithm:    sampling
 sample:       4000 (posterior sample size)
 priors:       see help('prior_summary')
 observations: 333
 predictors:   2

Estimates:
                    mean    sd      10%     50%     90%  
(Intercept)       -5873.6   314.8 -6279.8 -5874.8 -5478.8
flipper_length_mm    50.2     1.6    48.2    50.2    52.2
sigma               394.2    15.7   374.4   393.9   414.7

Fit Diagnostics:
           mean   sd     10%    50%    90% 
mean_PPD 4207.5   30.2 4168.6 4207.0 4246.7

The mean_ppd is the sample average posterior predictive distribution of the outcome variable (for details see help('summary.stanreg')).

MCMC diagnostics
                  mcse Rhat n_eff
(Intercept)       5.2  1.0  3624 
flipper_length_mm 0.0  1.0  3670 
sigma             0.3  1.0  3729 
mean_PPD          0.5  1.0  3463 
log-posterior     0.0  1.0  1778 

For each parameter, mcse is Monte Carlo standard error, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence Rhat=1).

summary(m_informatif_20)

Model Info:
 function:     stan_glm
 family:       gaussian [identity]
 formula:      body_mass_g ~ flipper_length_mm
 algorithm:    sampling
 sample:       4000 (posterior sample size)
 priors:       see help('prior_summary')
 observations: 333
 predictors:   2

Estimates:
                    mean    sd      10%     50%     90%  
(Intercept)       -5747.9   306.1 -6132.3 -5749.7 -5358.2
flipper_length_mm    49.5     1.5    47.6    49.6    51.4
sigma               394.3    15.7   374.7   394.0   414.6

Fit Diagnostics:
           mean   sd     10%    50%    90% 
mean_PPD 4208.1   30.9 4168.5 4207.9 4248.0

The mean_ppd is the sample average posterior predictive distribution of the outcome variable (for details see help('summary.stanreg')).

MCMC diagnostics
                  mcse Rhat n_eff
(Intercept)       5.1  1.0  3639 
flipper_length_mm 0.0  1.0  3650 
sigma             0.3  1.0  3745 
mean_PPD          0.5  1.0  3935 
log-posterior     0.0  1.0  1976 

For each parameter, mcse is Monte Carlo standard error, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence Rhat=1).

summary(m_informatif_10000)

Model Info:
 function:     stan_glm
 family:       gaussian [identity]
 formula:      body_mass_g ~ flipper_length_mm
 algorithm:    sampling
 sample:       4000 (posterior sample size)
 priors:       see help('prior_summary')
 observations: 333
 predictors:   2

Estimates:
                    mean    sd      10%     50%     90%  
(Intercept)       -1929.6   193.6 -2181.3 -1929.1 -1677.6
flipper_length_mm    30.5     1.0    29.3    30.5    31.8
sigma               480.8    20.0   455.5   480.1   507.0

Fit Diagnostics:
           mean   sd     10%    50%    90% 
mean_PPD 4206.8   36.6 4159.3 4207.2 4253.2

The mean_ppd is the sample average posterior predictive distribution of the outcome variable (for details see help('summary.stanreg')).

MCMC diagnostics
                  mcse Rhat n_eff
(Intercept)       3.5  1.0  3051 
flipper_length_mm 0.0  1.0  3052 
sigma             0.3  1.0  3311 
mean_PPD          0.6  1.0  3476 
log-posterior     0.0  1.0  1990 

For each parameter, mcse is Monte Carlo standard error, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence Rhat=1).

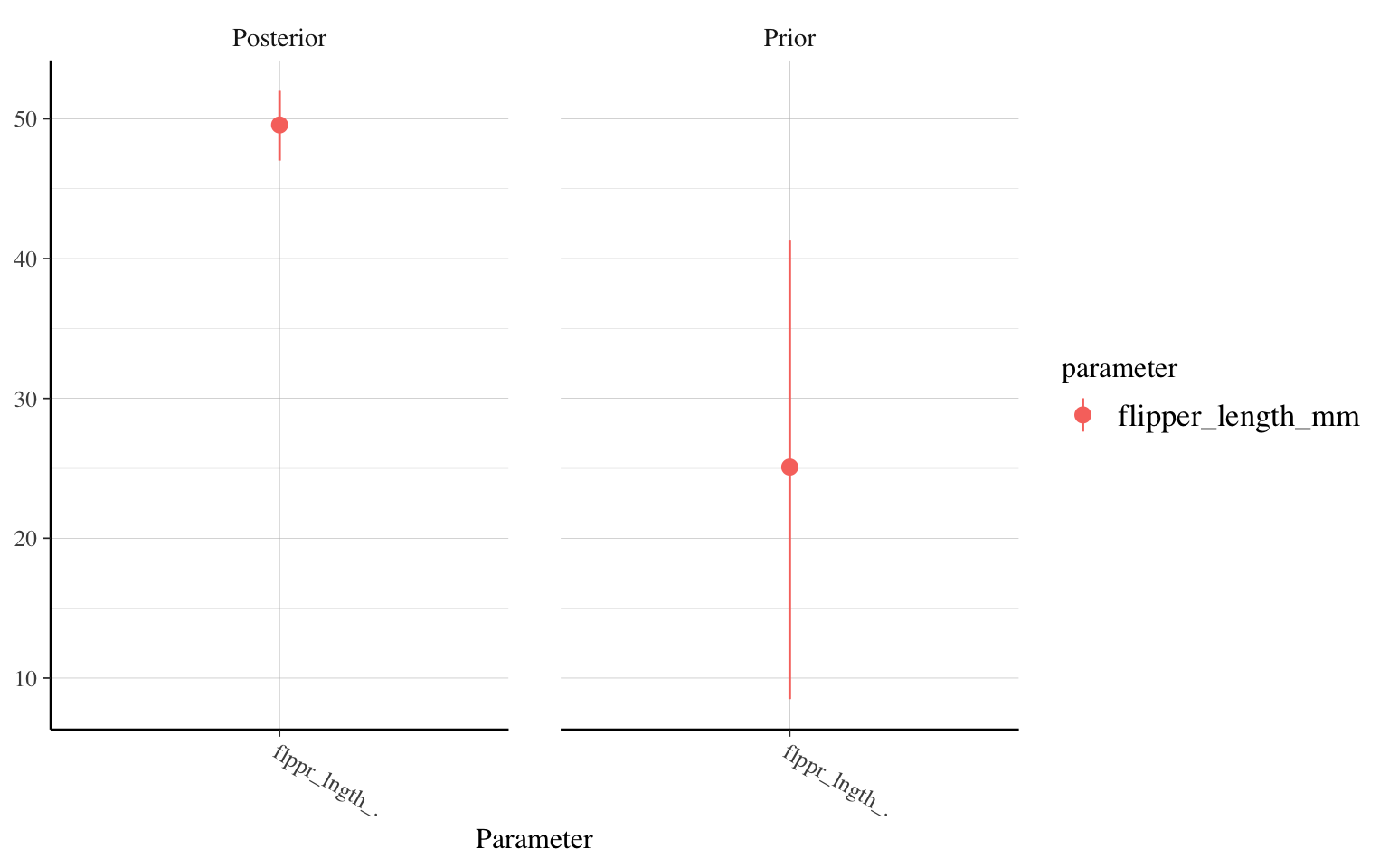
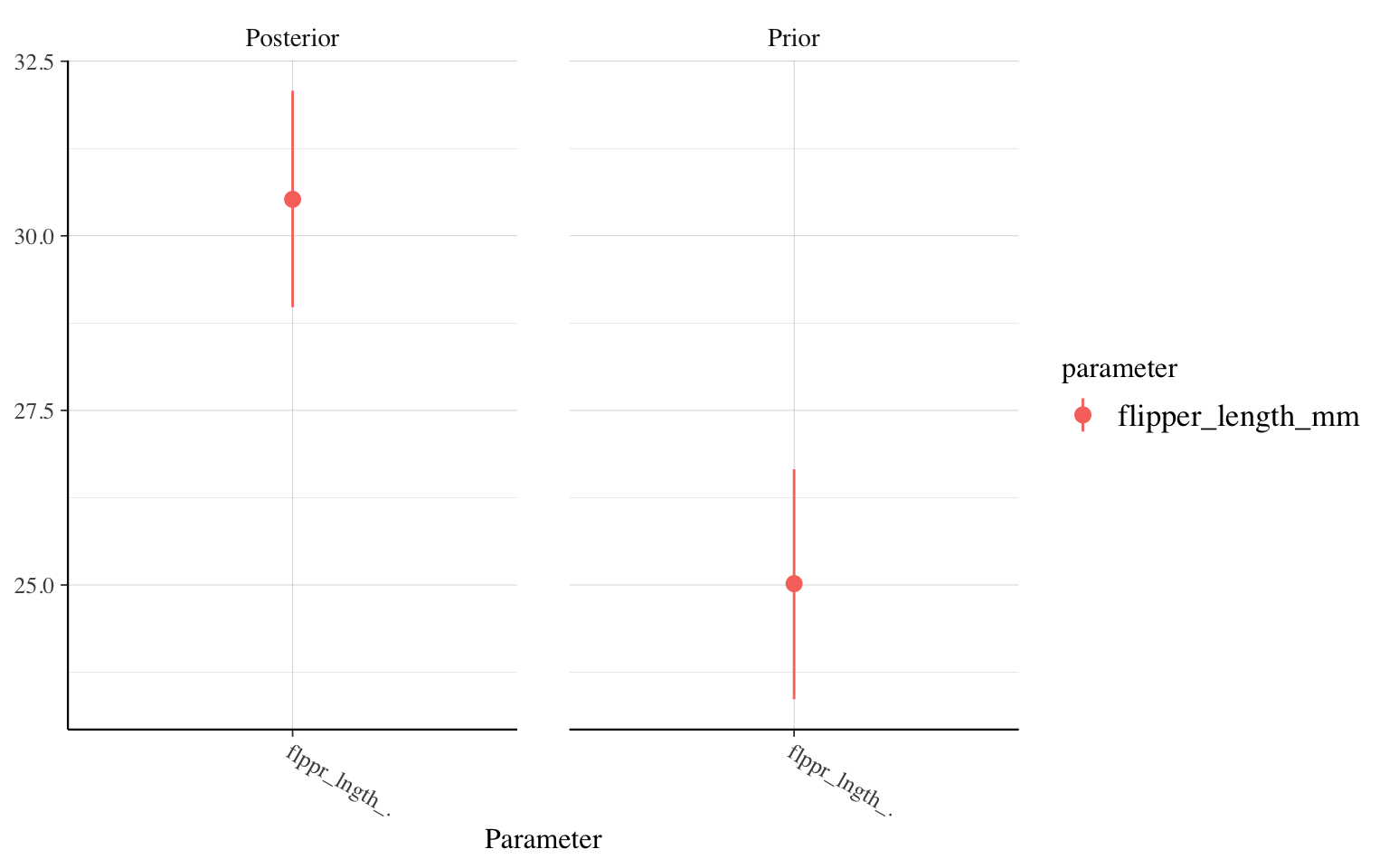
On constate donc qu’entre le modèle avec un a priori très vague et celui basé sur une étude préliminaire, il y a très peu de différence. Dans les deux cas, les nouvelles données fournissent beaucoup d’information comparé à nos connaissances antérieures. Par contre, dans le troisième modèle, qui utilise comme a priori une solide étude comportant 10 000 individus, la distribution a posteriori du paramètre est à 30 g/mm (vs. 50 g/mm pour les deux autres), car dans ce cas-ci, nos connaissances antérieures étaient très solides. Même si notre étude sur des centaines de manchots trouve une plus grande valeur, notre connaissance sur les manchots se modifie peu.

C’est là toute la puissance de l’approche bayésienne. Elle encapsule notre processus de mise à jour des connaissances. Si on a peu ou pas d’information sur le phénomène avant de débuter, l’analyse laisse parler les données. Mais si nos connaissances étaient solides, celles-ci seront difficiles à ébranler.

J’aime toujours penser à l’approche bayésienne avec des a priori informatifs comme une méta-analyse permanente. Chaque étude fait bouger la synthèse de nos connaissances. Proportionnellement à la quantité d’information connue avant et à celle fournie par les nouvelles données.

Les a priori faiblement informatifs

Même si à première vue les a priori non-informatifs sont attrayants par leur apparence d’objectivité, ils sont rarement les plus appropriés.

Tout d’abord, d’un point de vue technique, ils rendent la tâche de notre MCMC très complexe, puisque cette dernière doit explorer essentiellement de -Inf à +Inf pour chacun des paramètres. Aussi, ils ne sont pas très réalistes, puisque nous savons bien qu’il n’est pas aussi probable d’avoir une pente de 0 g/mm qu’une de 50 g/mm ou d’une de 5 000 000 g/mm. Juste par l’intervalle de poids et de longueur des ailes d’un manchot, nous savons que ce n’est pas possible.

Il existe donc un compromis, de plus en plus populaire, pour les cas où nous n’avons pas d’information précise comme une étude préliminaire, mais tout de même une idée de l’ordre de grandeur des possibles : les a priori faiblement informatifs. Pour faciliter leur compréhension, ces derniers sont souvent basés sur des données standardisées (i.e. centrées et réduites), et donc s’expriment en termes d’écart-type.

C’est la stratégie employée par stan_glm. À moins d’avis contraire (comme ci-haut), ce dernier place un a priori faible sur vos pentes, basé sur une distribution normale, avec une moyenne de 0 et un écart-type de 2.5, après avoir standardisé vos données. Donc, avant de lancer l’ajustement, le modèle assume qu’il y a 95% des chances que la pente (à l’échelle standardisée) se retrouve entre -5 et +5 écart-type de Y pour un écart-type de X. Ce chiffre, en apparence “ordinaire” est en fait extrêmement élevé.

Par exemple, la mesure d’effet standardisée du D de Cohen, qui est justement en écart-type de Y pour un changement d’un écart-type de X s’interprète comme un petit effet autour de 0.1, d’un grand effet autour de 0.8 et d’un immense effet autour de 2. Cette stratégie contraint donc les paramètres dans des fourchettes de valeurs raisonnables, tout en laissant amplement de liberté aux données de s’exprimer.

Comme la distribution normale s’étend de -Inf à +Inf, si jamais vous trouvez LA relation de fou avec une pente standardisée de 10 ou 50 écart-types, le modèle sera tout de même capable de l’ajuster, pour autant que vous ayez les données pour l’appuyer. Sinon, le modèle restera sceptique, comme vous devriez le demeurer aussi.

À quel point les nouvelles données changent nos connaissances?

Une des façons les plus directes d’observer si les données recueillies sont parlantes ou non est de comparer côte à côte la distribution a priori et la distribution postérieure de nos paramètres. Dans rstanarm, la fonction posterior_vs_prior permet d’automatiser cette tâche.

Comparons par exemple l’évolution du paramètre pour l’effet de la longueur des ailes, entre notre modèle avec un peu d’information (n=20) et notre modèle avec beaucoup d’information (n=10000) :

posterior_vs_prior(m_informatif_20,"flipper_length_mm")


posterior_vs_prior(m_informatif_10000,"flipper_length_mm")

La morale des distributions a priori

La chose à retenir de cette discussion à propos des distributions a priori est donc que ces dernières sont une façon d’être transparent par rapport à vos assomptions. À définir ce que vous connaissez du phénomène avant de commencer. Ce n’est pas une façon de “tricher” ou de manipuler les résultats. Le processus bayésien d’estimation des paramètres est conçu expressément pour mettre à jours des connaissances en se basant sur de nouvelles données. Il est fait pour laisser parler vos données.

Est-ce que mes a priori ont du sens?

Une chose importante à se demander lorsque l’on applique des distributions a priori à nos modèles est : est-ce que ces distributions ont du sens pour comprendre le phénomène à l’étude. On ne parle pas ici de d’utiliser les données du projet pour calculer à l’avance des distributions a priori, cela serait très dangereux : une forme grave de surajustement.

Cependant, il faut absolument jeter un coup d’oeil aux relations qui sont implicites dans nos a priori. Il faut se demander : est-ce réaliste ou non que l’on observe de telles relations. Le moindrement que vos modèles se compliqueront, il peut devenir impossible de gérer mentalement ce genre de question. C’est pourquoi il est habituellement recommandé de faire une vérification des prédictions a priori (prior predictive check). Le principe de cette technique est de piger des données, non pas dans la distribution postérieure, mais directement dans la distribution a priori.

Dans rstanarm, on peut y arriver directement en ajustant notre modèle avec un argument supplémentaire :

a_priori_10000 <- stan_glm(
  body_mass_g ~ flipper_length_mm, 
  data = manchots,
  prior = normal(location = 25,scale = 1),
  prior_PD = TRUE
)

On peut ensuite regarder par exemple la distribution des valeurs attendues de poids :

pp_check(a_priori_10000)

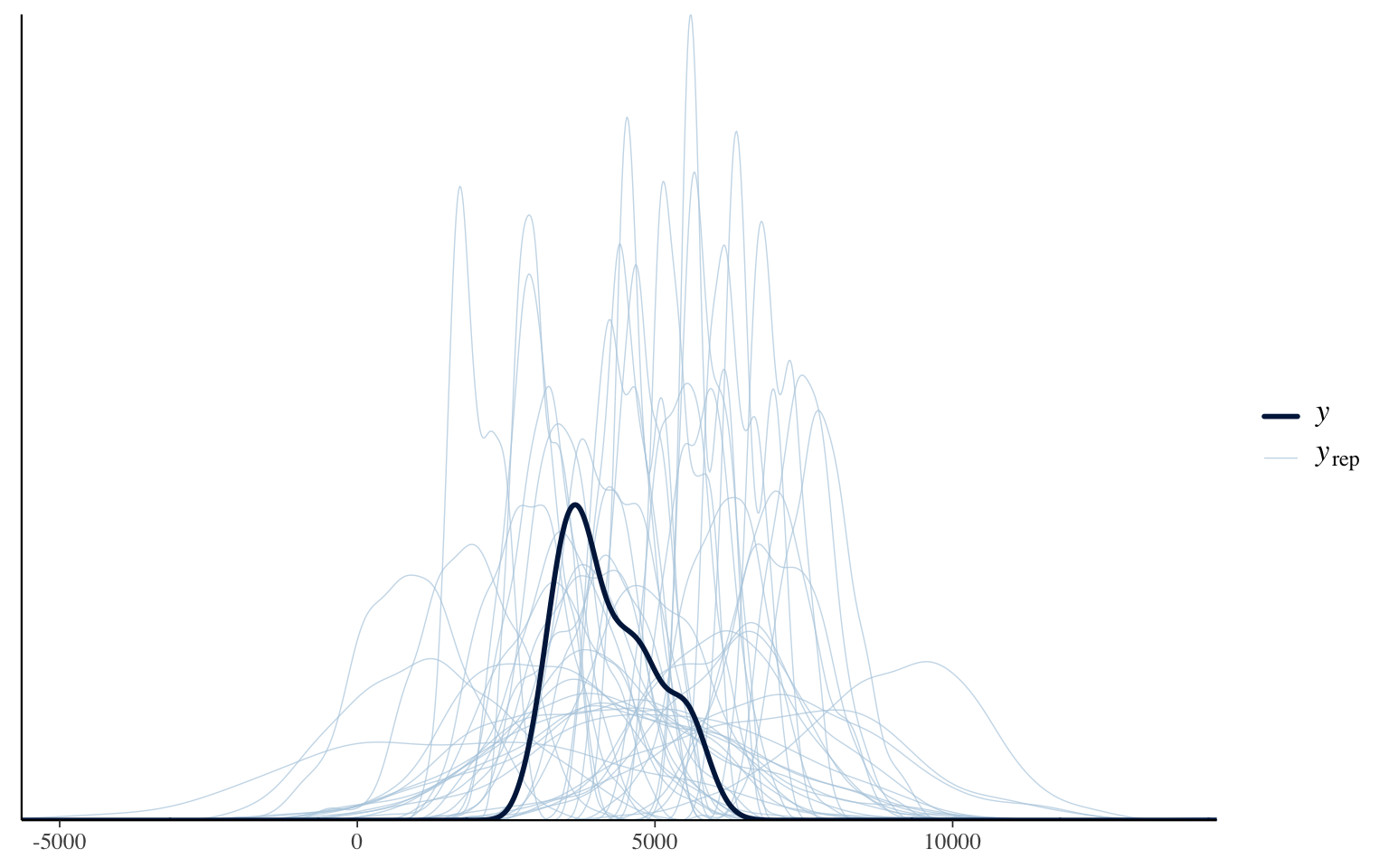
Évidemment ce n’est pas parfait. On retrouve quelques distributions de poids avec des valeurs < 0 et certaines centrées sur des poids 2x plus grands que les originaux. Mais ces instances sont très rares. La majorité des distributions auraient eu du sens écologiquement.

On aurait pu aussi extraire et tracer chacune des pentes (ou ici un échantillon de 100 pour que cela demeure lisible). L’objet a_priori_10000 contient déjà une série d’échantillons de paramètres, que l’on peut extraire en utilisant la fonction as.data.frame()

verif_pentes <- a_priori_10000 |> 
  as.data.frame() |> 
  janitor::clean_names() |> 
  sample_n(100)
head(verif_pentes)

   intercept flipper_length_mm      sigma
1 -2872.7168          24.82238  251.56464
2 -2065.1517          23.82648 1649.60026
3 -3229.8383          25.38553  485.41520
4  -907.2649          25.12735  366.63444
5 -2161.4786          25.30185  626.57642
6 -1154.2419          22.77948   27.41661

verif_pentes |> 
  ggplot() +
  geom_abline(aes(
    slope = flipper_length_mm, 
    intercept = intercept)) +
  xlim(170,240) +
  ylim(2500,7000)

Remarquez que la couche geom_abline ne construit pas les limites du graphiques. Nous avons dû le faire manuellement.

Ici, les pentes sont très serrées autour de valeurs qui ont beaucoup de sens, puisque c’était notre modèle avec un a priori très fort.

Comparons maintenant avec les a priori faiblement informatifs par défaut dans rstanarm

stan_glm(
  body_mass_g ~ flipper_length_mm, 
  data = manchots,
  prior_PD = TRUE
) |> 
  as.data.frame() |> 
  janitor::clean_names() |> 
  sample_n(100) |>
  ggplot() +
  geom_abline(aes(
    slope = flipper_length_mm, 
    intercept = intercept)) +
  xlim(170,240) +
  ylim(2500,7000)

Vous voyez que l’a priori par défaut ne force rien sur notre modèle. Il est aussi probable qu’une pente soit positive que négative, et la majorité sont plutôt faibles, proche d’une pente de zéro. Certaines prédisent des poids extrêmement grands (on en devine plusieurs > 10 000g), mais en général, la majorité est très bien. C’est ce que l’on veut trouver.

Est-ce que ma MCMC a bien fonctionné?

Jusqu’ici, nous avons utilisé et expliqué très brièvement les MCMC, mais il est important de savoir que ces derniers n’arrivent pas magiquement toujours au bon résultat.

LA chose à vérifier est de savoir si chacune des chaînes a bien fonctionné. C’est-à-dire qu’elle a exploré convenablement le paysage autour de chaque paramètre, et n’est pas restée coincée dans une petite zone.

Vérification visuelle

On peut tout d’abord vérifier le mélange des chaînes visuellement, à l’aide, par exemple, de la fonction mcmc_trace de la librairie bayesplot :

library(bayesplot)
mcmc_trace(m_informatif_0)

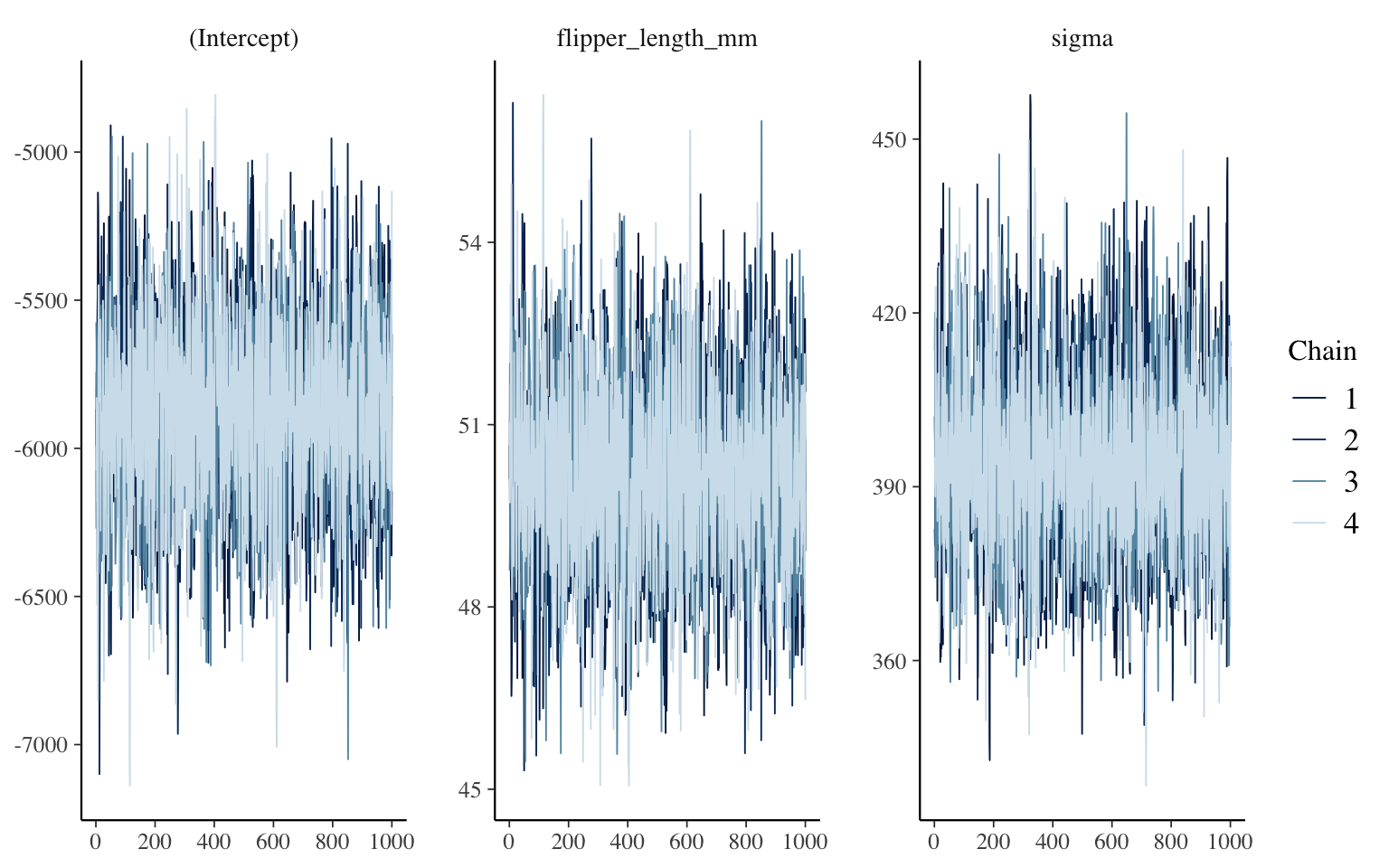
La fonction nous affiche donc le processus d’échantillonnage de la distribution postérieure, avec un panneau par paramètre. Ici, nous avons 4 chaînes, puisque si ne nous mentionnons rien, c’est le nombre de chaînes que rstanarm lance en parallèle. L’avantage d’utiliser plusieurs chaînes est que l’on peut voir si elles se sont comportées de façon équivalente, entre elles et sur l’ensemble du processus. Ce que l’on désire voir, pour chacune, est une sorte de chenille poilue, sur toute la largeur du panneau. Ce qui serait inquiétant de trouver serait, par exemple, qu’une des chaînes a seulement la moitié de la hauteur des autres, ou alors qu’elle part dans de très grandes valeurs pour quelques centaines d’itérations, etc.

R-chapeau?

Comme il peut être parfois difficile d’interpréter visuellement ces graphiques, une mesure, nommée R-hat (i.e. $\hat{R}$) a été inventé pour nous guider. De façon simple, cette dernière se calcule comme la racine carrée du rapport entre la variance totale des échantillons et la variance moyenne intra-chaîne. Si R-hat est près de 1, les chaînes sont bien mélangées et on peut se fier au résultat. Si la valeur s’éloigne de 1 (on cite souvent le seuil de 1.01), alors les chaînes ne sont pas bien mélangées. La distribution postérieure n’a pas bien été explorée et le résultat n’est pas utilisable. D’ailleurs, rstanarm vous affichera un avertissement si tel est le cas.

Ces valeurs sont accessibles à plusieurs endroits, par exemple à la fin du résumé de notre modèle :

summary(m_informatif_0)

Model Info:
 function:     stan_glm
 family:       gaussian [identity]
 formula:      body_mass_g ~ flipper_length_mm
 algorithm:    sampling
 sample:       4000 (posterior sample size)
 priors:       see help('prior_summary')
 observations: 333
 predictors:   2

Estimates:
                    mean    sd      10%     50%     90%  
(Intercept)       -5873.6   314.8 -6279.8 -5874.8 -5478.8
flipper_length_mm    50.2     1.6    48.2    50.2    52.2
sigma               394.2    15.7   374.4   393.9   414.7

Fit Diagnostics:
           mean   sd     10%    50%    90% 
mean_PPD 4207.5   30.2 4168.6 4207.0 4246.7

The mean_ppd is the sample average posterior predictive distribution of the outcome variable (for details see help('summary.stanreg')).

MCMC diagnostics
                  mcse Rhat n_eff
(Intercept)       5.2  1.0  3624 
flipper_length_mm 0.0  1.0  3670 
sigma             0.3  1.0  3729 
mean_PPD          0.5  1.0  3463 
log-posterior     0.0  1.0  1778 

For each parameter, mcse is Monte Carlo standard error, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence Rhat=1).

Vous voyez que toutes les valeurs de Rhat sont arrondies à 1.0.

Nombre d’échantillons effectif

Vous remarquez aussi dans cette sortie un autre outil de diagnostic : n_eff. n_eff mesure le nombre d’échantillons effectifs que vos chaînes ont produit, compte tenu de l’auto-corrélation temporelle présente dans les chaînes. Si ce nombre est particulièrement bas, il est signe que vous avez beaucoup ré-échantillonné la même zone de la distribution postérieure, et que vos conclusions ne sont probablement pas représentatives de sa vraie forme. Vous lirez souvent que l’on doit obtenir au moins 1000 échantillons effectifs pour avoir un portrait utilisable.

Solution aux problèmes avec le processus MCMC

La chose la plus simple à faire lorsque vous constatez des problèmes avec vos chaînes est de simplement leur demander d’échantillonner plus.

On pourrait par exemple demander à explorer 2000 échantillons par chaîne plutôt que 1000, comme ceci :

m2000 <- stan_glm(
  body_mass_g ~ flipper_length_mm, 
  data = manchots,
  prior = NULL,
  iter = 4000
)

summary(m2000)

Model Info:
 function:     stan_glm
 family:       gaussian [identity]
 formula:      body_mass_g ~ flipper_length_mm
 algorithm:    sampling
 sample:       8000 (posterior sample size)
 priors:       see help('prior_summary')
 observations: 333
 predictors:   2

Estimates:
                    mean    sd      10%     50%     90%  
(Intercept)       -5867.1   307.6 -6252.6 -5871.9 -5476.6
flipper_length_mm    50.1     1.5    48.2    50.2    52.0
sigma               394.8    15.4   375.6   394.2   414.9

Fit Diagnostics:
           mean   sd     10%    50%    90% 
mean_PPD 4206.3   30.7 4166.7 4206.6 4245.2

The mean_ppd is the sample average posterior predictive distribution of the outcome variable (for details see help('summary.stanreg')).

MCMC diagnostics
                  mcse Rhat n_eff
(Intercept)       3.6  1.0  7468 
flipper_length_mm 0.0  1.0  7499 
sigma             0.2  1.0  8193 
mean_PPD          0.4  1.0  7325 
log-posterior     0.0  1.0  3911 

For each parameter, mcse is Monte Carlo standard error, n_eff is a crude measure of effective sample size, and Rhat is the potential scale reduction factor on split chains (at convergence Rhat=1).

Remarquez que pour obtenir 2000 échantillons par chaîne, j’ai dû en demander 4000 au total, puisque, à moins d’avis contraire, rstanarm ordonne à l’algorithme d’utiliser la moitié des itérations pour évaluer les méta-paramètres de la chaîne (p. ex. de quelle taille faire les sauts entre les propostions, etc.), qu’il nomme le warm-up (réchaufement). Si nécessaire (par exemple si un avertissement vous le suggère), vous pouvez aussi modifier nombre d’itérations attitrées au réchauffement.

Ceci étant dit, la majorité du temps, si vous avez des ennuis avec vos chaînes, ce sera plutôt que votre modèle est mal spécifié. Est-ce que vos a priori ont du sens par rapport aux données. Avez-vous par exemple une observation valant 1 000 000, alors que votre a priori est spécifié comme $\sim \mathcal{N}(0,3)$ donc, à peu près impossible d’obtenir d’aussi grandes valeurs?

De là l’imporance de bien effectuer l’exploration de la distribution a priori.

Est-ce que mon modèle est bon?

Sans test d’hypothèses, vous vous sentirez peut-être un peu au dépourvu pour évaluer la qualité de votre modèle statistique!

Comme mentionné plus haut, la première chose à se rappeler est que, si vos chaînes ont correctement échantillonné la distribution postérieure, votre modèle EST interprétable. Vos paramètres répondent à la question : en assumant ce modèle et les données mesurées, voici les valeurs les plus probables pour chacun des paramètres du modèle. Donc, la question ici n’est pas de tester le modèle comme tel, mais de l’explorer.

Un des premiers outils à votre disposition est de regarder si la distribution des prédictions, basée sur la distribution postérieure des paramètres, reconstruit adéquatement la distribution originale de la variable expliquée. Cette technique se nomme en anglais posterior predictive check.

pp_check(m_informatif_0)

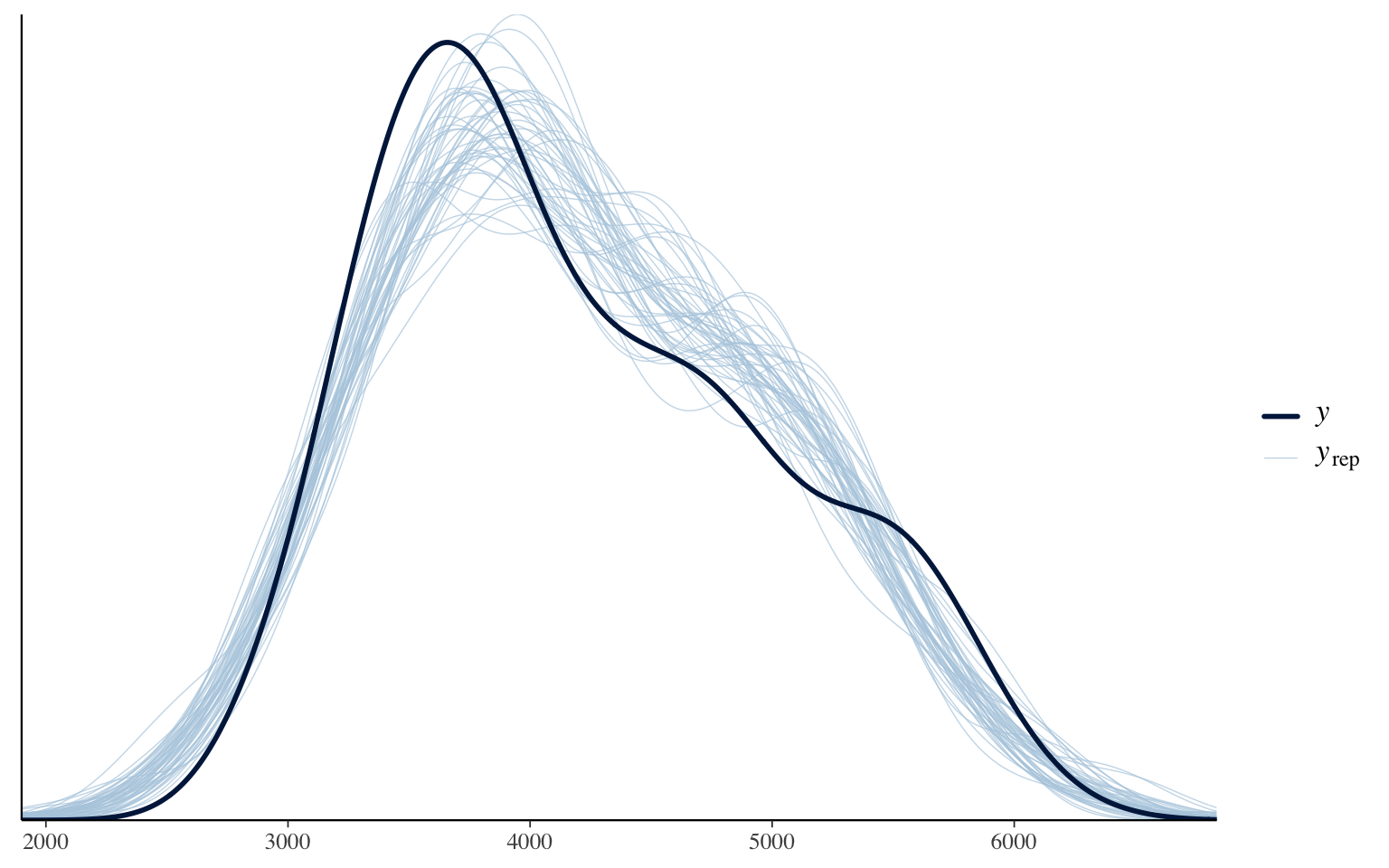
Ce graphique compare la distribution (lissée) originale des données (la ligne noire) avec la distribution des prédictions pour chacune des combinaisons de paramètres testées par le modèle. En général, notre modèle parvient adéquatement à reproduire la distribution originale. Je vous rappelle, encore ici, il ne s’agit pas d’un test, mais d’une exploration. Si jamais des particularité des données ne sont pas bien reproduites ou la forme générale n’est pas respectée, c’est un signe qu’un meilleur modèle peut probablement être conçu pour ces données.

Est-ce que ce modèle est meilleur qu’un autre?

Après avoir exploré l’ajustement de votre modèle, vous voudrez probablement savoir si ce dernier est une amélioration ou non par rapport à d’autres modèles que vous avez testés. Est-ce que vous avancez dans la bonne direction ou non?

Pour ce faire, il faudra s’entendre sur une façon de mesurer la qualité du modèle. Un des dilemmes que vous connaissez peut-être à propos de la qualité des modèles statistiques est que ces derniers peuvent finir par être surajustés aux données trouvées. Avec suffisamment de paramètres, on peut reproduire n’importe quel jeu de données, avec précision, perfection même. Mais ce modèle parfait ne serait d’aucune utilité car devant de nouvelles données, il serait entièrement dépourvu. L’adage dit d’ailleurs : il est facile d’ajuster, mais difficile de prédire (fitting is easy, predicting is hard). Or, ce que l’on veut, c’est un modèle qui peut prédire correctement. C’est là uniquement qu’il devient utile.

C’est pourquoi la façon recommandée d’évaluer la qualité d’un modèle statistique est d’utiliser la validation croisée. Dans sa version la plus extrême, cette stratégie consiste à ajuster le modèle avec toutes les données sauf une. Ensuite, on évalue la qualité de la prédiction pour la donnée mise de de côté. Puis on recommence le stratagème avec chacune des données! En anglais, cette technique se nomme leave-one-out cross validation (loo-cv).

Avec des modèles simples, rapides d’ajustement, il peut être relativement facile de coder la validation croisée dans une boucle et la faire rouler en quelques secondes. Dans la vraie vie, cette façon de faire est cependant rarement pratique. Même si votre modèle est relativement rapide à ajuster, par exemple 30 secondes par ajustement, cette opération pourrait prendre tout de même des dizaines d’heures si vous avez quelques milliers d’observations, ce qui n’est pas rare.

WAIC

Vous ne le savez peut-être pas, mais l’AIC (le critère d’information d’Akaike) a justement été conçu comme une approximation, un raccourci, pour obtenir l’information d’une validation croisée, sans la charge computationnelle qu’elle implique. À de grandes tailles d’échantillon, l’AIC et la loo-cv fourniront exactement le même classement pour une série de modèles.

Il existe, pour l’approche bayésienne, un algorithme semblable à l’AIC, le WAIC, qui prend en compte correctement le fait que notre modèle bayésien nous fournit une série de valeurs de paramètres plutôt qu’une valeur directe. Ce dernier peut être utilisé de la même façon que l’AIC, avec les delta-AIC, le poids d’Akaike permettant de déterminer la probabilité que chaque modèle soit le meilleur, etc.

Il n’est cependant pas à l’heure actuelle l’indice recommandé pour comparer des modèles entre eux, car un autre algorithme, PSIS-LOO-CV permet de faire presque constamment un travail plus précis, en plus d’informer directement l’utilisateur lorsque ses valeurs deviennent imprécises/dangereuses à l’utiliser.

PSIS-LOO-CV

Comme pour l’AIC, PSIS-LOO-CV est un algorithme permettant d’obtenir les résultats de la validation croisée sur un modèle, sans devoir le ré-ajuster pour chacune des prédictions.

L’idée générale est qu’il est possible pour chaque observation et pour chaque échantillon de paramètres de mesurer la probabilité d’observer cette valeur. L’inverse de cette probabilité sera donc le poids de sa contribution au modèle. Plus une observation est surprenante, plus elle aura eu d’influence. Ensuite, plutôt que de considérer chaque échantillon de paramètres comme égal dans les calculs de moyennes, on les pondère par le poids de chaque observation. On nomme cette technique l’échantillonnage par importance (importance sampling).

Un des problèmes avec cette stratégie est que les poids ne sont pas nécessairement fiables. Si ils sont particulèrement grands, ils peuvent dominer le calcul. On pourrait évidemment couper les poids au-delà d’un seuil, mais cela aussi créerait un biais dans le calcul. La clé pour régler ce problème est que, selon la théorie, les grandes valeurs de poids devraient suivre une distribution de Pareto pour chaque observation. L’algorithme PSIS-LOO-CV (Pareto-Smoothed Importance Sampling) remplace donc les grands poids par les valeurs lissées, prédites par la distribution de Pareto pour cette observation.

L’avantage principal de cette méthode par rapport au WAIC est qu’il fournit pour chaque observation le paramètre k de la distribution de Pareto qui a été estimée, et que ce dernier peut être utilisé pour

  1. Identifier les valeurs influentes (les grandes valeurs de k)
  2. Identifier les moments où la valeur de PSIS-LOO-CV n’est pas fiable. La queue de la distribution de Pareto devient extrêmement large au delà de k > 0.5, et donc les estimations associées moins fiables. Des simulations suggèrent que les valeurs de PSIS-LOO-CV ne sont plus utilisables au delà de k > 0.7, et vous obtiendrez d’ailleurs des avertissements le moment venu.

Par contre, comme l’AIC, la valeur de PSIS-LOO-CV d’un seul modèle n’est absolument pas informative et ne peut pas être interprétée comme la qualité du modèle comme tel. Il s’agit d’une mesure relative de la qualité.

Exemple d’utilisation

Afin de voir comment appliquer la comparaison de modèles avec PSIS-LOO-CV, nous allons comparer le modèle du début de l’atelier qui comportait 4 variables à celui utilisé pour les a priori, qui en contenait une seule.

loo(m_bayes)

Computed from 4000 by 333 log-likelihood matrix.

         Estimate   SE
elpd_loo  -2366.7 12.3
p_loo         6.6  0.5
looic      4733.3 24.7
------
MCSE of elpd_loo is 0.0.
MCSE and ESS estimates assume MCMC draws (r_eff in [0.5, 1.2]).

All Pareto k estimates are good (k < 0.7).
See help('pareto-k-diagnostic') for details.

loo(m_informatif_20)

Computed from 4000 by 333 log-likelihood matrix.

         Estimate   SE
elpd_loo  -2464.1 13.1
p_loo         2.9  0.3
looic      4928.3 26.2
------
MCSE of elpd_loo is 0.0.
MCSE and ESS estimates assume MCMC draws (r_eff in [0.8, 1.0]).

All Pareto k estimates are good (k < 0.7).
See help('pareto-k-diagnostic') for details.

Alors, première chose à savoir : PSIS-LOO-CV mesure la précision des prédictions. Donc, plus la valeur est élevée, meilleur est le modèle. Ici, le modèle m_bayes, qui contient 4 variables, produit de meilleures prédictions que celui avec une seule variable. Sa valeur de elpd_loo (un autre nom pour PSIS-LOO-CV) est -2464.1 vs -2366.7.

Comme nous avons l’ensemble des échantillons, l’algorithme a aussi pu calculer la variabilité autour de notre estimé de PSIS-LOO-CV, soit de 13.1 d’un côté et 12.3 de l’autre.

On peut donc se demander quelle est la vraie différence entre ces modèles. Nous pourrions nous même aller récupérer les chiffres pour chacun des échantillons de paramètres, mais la fonction loo_compare le fera automatiquement pour nous :

loo_compare(loo(m_bayes), loo(m_informatif_20))

                elpd_diff se_diff
m_bayes           0.0       0.0  
m_informatif_20 -97.5      11.6

Donc, la différence moyenne de PSIS-LOO-CV entre nos deux modèles est de -97.5 points, avec une erreur-type de 11.6 points. La différence est vraiment claire entre les deux modèles.

Conclusion

Et c’est tout. Ce n’est pas plus compliqué que cela de faire la transition à l’analyse bayésienne en 2025.

Vous avez maintenant les bases pour :

Nous n’avons, évidemment, fait d’effleurer la surface du potentiel de cette approche. Pour la suite des choses, plusieurs chemins s’offrent à vous :